A Stochastic Model
of the Long-Range Financial Status
of the OASDI Program—September 2004

V. APPENDICES

B. TIME-SERIES ANALYSIS

1. Background

Time-Series Modeling

Time-series analysis is a standard projection technique in econometric modeling. The equations used to project the assumptions are fit using these techniques. This appendix provides details about the models in general, presents statistical methods employed to test these models, and underscores the nuances inherent in the method of determining the equations. The reader may wish to consult Box, Jenkins and Reinsel (1994) or Hamilton (1994) for a standard presentation of this material. A more elementary reference is Pindyck and Rubinfeld (1998).

Stationary Time Series

A time series Y_t is stationary if neither the mean nor variance depends on time t:

In particular, the variance of Y_t is always equal to σ² = γ₀ . A different concept is that of strict stationarity. This means that any k values of the time series have the same joint distribution as any other set of k values of the time series. If a time series Y_t is strictly stationary, then it is stationary. Henceforth, when we say that a time series Y_t is stationary we intend that it is strictly stationary. However, it is more straightforward to think of a time series as stationary in the simpler sense.

White Noise Process

Suppose that ε_t, the error term at time t, is normally distributed with mean zero and constant variance σ_ε². If ε_r and ε_s are uncorrelated for r ≠ s, then the series ε_t is called a white noise process.

Random Walk

The simplest of all time-series models is the random walk. Here, if Y_t is the series to be estimated, then the random walk process is given by Y_t = Y_t-1 + ε_t . The error term series, ε_t , is a white noise process. The forecast error variance increases as a linear function of the forecast lead time, l. In other words, the variance of the l-step-ahead forecast error is lσ_ε². The confidence intervals for these forecasts will therefore widen as l increases.

Moving Average (MA) Models

A time series is called a moving average model of order q, or simply an MA(q) process, if

Y_t = µ + ε_t –θ₁ε_t-1 –θ₂ε_t-2 –…–θ_qε_t-q .

In this equation, θ₁,…,θ_q are constant parameters and µ is the process mean. The error term series, ε_t, is a white noise process.

Autoregressive (AR) Models

A time series is called an autoregressive model of order p, or simply an AR(p) process, if

Y_t = φ₁Y_t-1 + φ₂Y_t-2 +…+φ_pY_t-p + δ + ε_t .

In this equation φ₁,…,φ_p are constant parameters and δ is a drift term. The naming of this model is apt because the coefficients of the time-series equation are obtained by regressing the equation on itself, more precisely, with its own p lagged values. The error term series, ε_t, is a white noise process. If this time series is stationary, then the mean μ of this process is computed to be

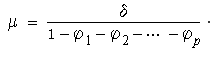
Autoregressive Moving Average (ARMA) Models

As its name indicates, an autoregressive moving average model of order (p,q), or simply an ARMA(p,q) model, is a natural combination of an autoregressive and moving average model. The equation which specifies an ARMA(p,q) model takes the form

Y_t = δ + φ₁Y_t-1 + φ₂Y_t-2 +…+ φ_pY_t-p + ε_t –θ₁ε_t-1 –θ₂ε_t-2 –…–θ_qε_t-q .

Deviations Form of ARMA Model Equations

It is often more convenient to transform an ARMA model equation into deviations form using the equation

y_t = Y_t – μ,

where μ is defined, as above, to be the mean of the process. The transformed model may be written as

y_t = φ₁y_t-1 + φ₂y_t-2 +…+ φ_py_t-p + ε_t –θ₁ε_t-1 –θ₂ε_t-2 –…–θ_qε_t-q ,

and has a mean of zero.

Adding the original process mean to both sides of the equation produces

Y_t = μ + φ₁y_t-1 + φ₂y_t-2 +…+ φ_py_t-p + ε_t –θ₁ε_t-1 –θ₂ε_t-2 –…–θ_qε_t-q .

The lagged variables are left in deviations form, and the constant term, μ, on the right-hand side is the process mean.

Cholesky Decomposition

Suppose 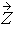= (Z₁,…, Z_n)´ is a vector of independently and identically distributed standard normal random variables. (If A is a matrix, then A´ denotes its transpose.) Suppose we want to use these random variables to obtain a random vector 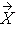 = (X₁,…, X_n)´ from a multivariate normal distribution with mean 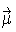 = (µ₁,…, µ_n)´ and an n×n variance-covariance matrix V = (σ_ij) [with σ_ij = Cov(X_i, X_j) for i, j = 1,…, n]. Since V is positive definite and symmetric, a standard result in linear algebra yields a lower triangular matrix, L, such that V = LL´. The random vector X = 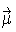 + L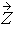 is then a random vector with the desired properties. The decomposition V = LL´ is called a Cholesky decomposition; see Atkinson (1989) for more details. In what follows we call the matrix L a Cholesky matrix.

For our applications, a Cholesky decomposition is used to convert a random vector, 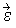of independent standard normal variates to a multivariate normal distribution with mean 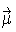 =  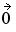(the zero vector) and a variance-covariance matrix V obtained by using historical data. If L is a lower triangular Cholesky matrix associated with V then the vector L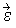 has the required multivariate normal distribution.

Vector Autoregressive Models

Vector autoregressive models allow the joint modeling of time-series processes. For the sake of simplicity, suppose that three variables y_1,t ,  y_2,t , and  y_3,t depend on time t. Data may indicate that these variables may be related to each other's past values. The simplest such case is when the relationship is limited to the time-1 lag, i.e., when y_1,t ,  y_2,t , and  y_3,t may be modeled in terms of  y_1,t-1,  y_2,t-1, and  y_3,t-1. In this case, a three-variable VAR(1) model takes the form

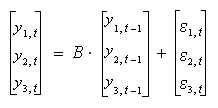
for some 3×3 matrix B.

Alternatively stated, if 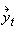 = (y_1,t, y_2,t, y_3,t)´ and 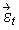 = (ε_1,t, ε_2,t, ε_3,t)´ then the model takes the form 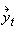 = 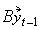+ 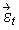for some 3×3 matrix B.

The k-variable VAR(p) model, with p lags, naturally extends from this. If 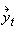 = (y_1,t, y_2,t,…, y_k,t)´ and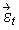
 = (ε_1,t, ε_2,t,…, ε_k,t)´, then the k-variable VAR(p) model takes the form 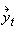 = 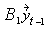++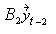…++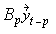 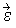for k×k matrices B₁,…, B_p.

2. Methods

Modified Autoregressive Moving Average (ARMA) Models

The equations used to model the assumptions are autoregressive moving average models with the additional requirement that the mean of the variable Y_t is always equal to its value under the TR04II. The value of the variable under the TR04II is written Y_t^TR. Thus, the mean of Y_t varies, in general, in the early years of the long-range period. The resulting model is called a modified autoregressive moving average model. In general, the equation in a modified autoregressive moving average model takes the form

Y_t = δ_t + φ₁Y_t-1 + φ₂Y_t-2 +…+ φ_pY_t-p + ε_t –θ₁ε_t-1 –θ₂ε_t-2 –…–θ_qε_t-q .

Writing this equation in "deviations form," with y_t = Y_t – μ_t gives

Y_t = μ_t + φ₁y_t-1 + φ₂y_t-2 +…+ φ_py_t-p + ε_t –θ₁ε_t-1 –θ₂ε_t-2 –…–θ_qε_t-q .

Since μ_t = Y_t^TR, we obtain the expression

Y_t = Y_t^TR + φ₁y_t-1 + φ₂y_t-2 +…+ φ_py_t-p + ε_t –θ₁ε_t-1 –θ₂ε_t-2 –…–θ_qε_t-q .

Equations in Chapter II are all presented in this form, with the letters Y and y replaced with a more suggestive naming.

Return to list of Studies.