Factors Affecting Initial Disability Allowance Rates for the Disability Insurance and Supplemental Security Income Programs: The Role of the Demographic and Diagnostic Composition of Applicants and Local Labor Market Conditions
Social Security Bulletin, Vol. 72, No. 4, 2012 (released November 2012)
Various factors outside the control of decision makers may affect the rate at which disability applications are allowed or denied during the initial step of eligibility determination in the Social Security Disability Insurance (DI) and Supplemental Security Income (SSI) programs. In this article, using individual-level data on applications, I estimate the role of three important factors—the demographic characteristics of applicants, the diagnostic mix of applicants, and the local unemployment rate—in affecting the probability of an initial allowance and state allowance rates. I use a random sample of initial determinations from 1993 through 2008 and a fixed-effects multiple regression framework. The empirical results show that the demographic and diagnostic characteristics of applicants and the local unemployment rate substantially affect the initial allowance rate. An increase in the local unemployment rate tends to be associated with a decrease in the initial allowance rate. This negative relationship holds for adult DI and SSI applicants and for SSI childhood applicants.
Kalman Rupp is a senior economist with the Division of Policy Evaluation, Office of Research, Evaluation, and Statistics, Office of Retirement and Disability Policy, Social Security Administration.
Acknowledgments: The author is indebted to Brad Trenkamp for assistance in assembling the database for this study and is also thankful to Norma Coe, Jessie Dalrymple, Paul Davies, Eli Donkar, Irena Dushi, Jeff Hemmeter, Bert Kestenbaum, and Alexander Strand for helpful feedback, useful suggestions, and technical review comments on earlier versions of the article.
Contents of this publication are not copyrighted; any items may be reprinted, but citation of the Social Security Bulletin as the source is requested. The findings and conclusions presented in the Bulletin are those of the authors and do not necessarily represent the views of the Social Security Administration.
The original print and web versions of this article contained an error in the notes for Table 5. The independent variables listed for Model 6 (sets 1 and 2) should have included “unemployment rate.” The corrected note now appears in the web versions of this article. [Posted: July 6, 2015.]
Introduction
| DDS | Disability Determination Service |
| DI | Disability Insurance |
| GLS | generalized least squares |
| OLS | ordinary least squares |
| SSA | Social Security Administration |
| SSI | Supplemental Security Income |
The probability of an initial disability allowance among Disability Insurance (DI) and Supplemental Security Income (SSI) applicants is affected by numerous factors at individual, state, and national levels. That includes demographic and diagnostic characteristics of applicants (age, sex, and type of impairment), national policies, local factors such as the state unemployment rate, and the implementation of disability determination policies by state Disability Determination Services (DDSs). In this article, I focus on the role of key factors that are outside of the direct control of DDS management in affecting initial allowances. I also discuss implications for the understanding of variations in state initial allowance rates.1
Three of the most important factors believed to affect the probability of an initial allowance are (1) demographic characteristics of applicants, (2) the diagnostic mix of applicants, and (3) local labor market conditions. Existing descriptive statistical tabulations of initial determination results summarize the association of those variables and the initial allowance rate, but are not designed to isolate the independent effect of those factors. More is known about the causal effect of labor market shocks on the allowance rate. Consistent with previous studies (discussed in the next section), I use fixed-effects multiple regression analysis. The fixed-effects model controls for state- and/or year-specific effects. This nonexperimental methodology allows the estimation of the relationship between the dependent variable (initial allowance rate) and the independent variables of interest net of long-term differences among states and changes in national policies affecting each state. Because of the use of individual-level data on applicants, I can look at the relationship between my indicator of local labor market conditions—the unemployment rate—and the initial allowance rate, considering a level of detail on applicant characteristics (for example, age and diagnostic category) that has not been feasible in previous work that was based exclusively on state-level data. Because in this study (as in all related analyses) the nature of the evidence is nonexperimental, caution is warranted in causal interpretation.
There are a number of reasons for expecting a relationship between labor market conditions, disability applications, and the initial allowance rate. Adverse labor market conditions are expected to bring in marginally qualifying or marginally interested applicants or affect the timing of application following disability onset. Adverse labor market conditions may result in job loss or decreased access to full-time, part-time, or irregular job or work opportunities.2 Those changes typically hit people with disabilities the hardest. Thus, people in the process of disablement may apply for disability benefits earlier than they otherwise would. Others may believe that they are only marginally qualified, but the opportunity cost of applying for disability benefits decreases sufficiently for application to appear worthwhile. A related, but distinct factor is that reduced employment and earnings increase the chances for an adult applicant to pass the substantial gainful activity (SGA) screen. These factors are relevant in the DI and SSI adult program context. The loss of income and reduced work opportunities also increase the chances that the individual would meet the SSI income screen. That factor affects adult SSI and concurrent applicants. Concurrent applicants meet the eligibility criteria of both DI and SSI, and thus are potentially eligible to receive both types of benefits. Job loss, poor labor market conditions, and the increased chance of meeting the SSI means test because of parental income loss may also affect adults with disabled children by increasing the relative attractiveness of applying for disability benefits on behalf of their child. An increase in the proportion of marginally qualified applicants is outside of the control of the DDS and should be expected to result in a reduced average probability of allowance. A negative relationship between changes in the unemployment rate and the probability of an initial allowance suggests that the Social Security Administration (SSA) is successful in screening out some marginally qualified applicants. The present study has been designed to address the overall relationship between the unemployment rate and the initial allowance rate. In this study, I do not test specific mechanisms underlying that relationship, although that is a worthwhile topic for more research in the future.
This study focuses on the initial disability determination outcome (initial allowance or initial denial).3 Thus, when I speak of "applicants" in the context of this analysis, I am referring to people subject to the initial determination decision.4 I refer to Title II of the Social Security Act as "DI" and Title XVI as "SSI." People applying for or receiving both DI and SSI benefits are referred as "concurrents" throughout this article. Adults who apply for benefits are classified as "DI-only," "SSI-only," or "concurrent" applicants.
The rest of the article is structured as follows: I review related literature in the next section and then address the data and methodology. I then present the empirical results and finally conclude.
Previous Literature
A paucity of research addresses factors affecting disability allowance rates. However, a larger body of previous research looks at factors affecting applications and awards. The broader literature is relevant for my topic for several reasons. First, key hypotheses about the effects of labor market conditions on initial allowance rates are predicated on the presumption of a positive relationship between adverse labor market conditions and disability applications. Second, separate estimates of the effects of labor market conditions on applications and on initial allowances is informative with respect to possible effects of labor market conditions on initial allowance rates. For example, if an estimated positive relationship exists between changes in the state unemployment rate and changes in the volume of disability applications, and a similar but smaller effect with respect to the volume of initial allowances, such a finding would suggest a negative relationship between high unemployment and the initial allowance rate. Finally, the methodological issues are similar with respect to estimating the effect of various factors on applications, allowances, and allowance rates.
Rupp and Stapleton (1995) summarized studies on the relationship between the unemployment rate, applications, awards, and caseload growth between 1974 and 1995, using primarily aggregate time-series methods and, in a few instances, cross-sectional approaches based on individual-level data. In addition, they presented new results based on state-level, fixed-effects modeling. Their fixed-effects analysis also provided much more detail and programmatic specifics than did previous studies. Specifically, while previous studies were limited to DI applications and awards, the authors also estimated models of initial determinations and the initial allowance rate separately for DI-only, SSI-only, and concurrent applicants. The fixed-effects results generally have shown a positive relationship between the state unemployment rate and both DI and SSI applications and awards. The estimates for initial allowance rates have shown zero effect in the year of change, but significant negative effects with lags of 1 year and 2 years for all three program groups. A lagged effect arises if changes in the unemployment rate resulted in increased applications in subsequent years. The authors estimated that a 1 percentage point increase in the unemployment rate was associated with no change in the initial allowance rate for DI-only applicants in the given year of the unemployment rate change, but it resulted in a 1 percentage point decrease in the initial allowance rate during the following year as well as during the second year after the unemployment rate change. Stapleton, Dietrich, and Lo (1995) and Stapleton and others (1998) provided detail on the data and methodology that was used to estimate the results reported previously by Rupp and Stapleton (1995).
Using individual-level data on a sample of men from the 1978 Survey of Disability and Work and a structural model of applications, awards, and state-contingent lifetime income flows, Kreider (1999) estimated, as expected, that the unemployment rate has had a positive effect on DI applications. Black, Daniel, and Sanders (2002) used county-level data; a natural experiment framework; and first differences with state, county, and year fixed effects to estimate the effect of labor market shocks to the local economy on program participation. The authors found a negative relationship between labor market participation and disability program participation both for DI and SSI.5 Their results suggested that the relationship between economic conditions and disability program participation is much stronger for permanent than for transitory economic shocks. Transitory shocks reflect short-term (for example, year-to-year) changes—such as typical business cycle effects—while permanent shocks are associated with lasting change, such as the disappearance of a major source of jobs in the local economy or the coal boom and bust studied by the authors. Burkhauser, Butler, and Weathers (2001/2002) used Health and Retirement Study data and a hazard model framework to analyze the effect of various factors on the timing of DI applications. They used the unemployment rate to capture the effects of labor market conditions on a worker's decision to apply for DI. Their results showed that a higher state unemployment rate substantially increases the risk of DI application following the onset of disability for both men and women and reduces the time from disability onset to application.
Strand (2002) used state-level data to assess variation in allowance rates for the 1997–1999 period. He used ordinary least squares (OLS) regression, which pooled the 3 years of data, with the allowance rate (and in some models, the filing rate) as the dependent variable, a number of state-level predictors, and year dummies. The models explained a substantial portion of state-to-state variation, and when adjusting for the independent variables, the variation in allowance rates among states was cut in half. The author also found that states with the highest and lowest allowance rates for DI and SSI tended to retain that status over time and that there was a negative association between filing rates and allowance rates. The unemployment rate coefficients were negative, as expected, and statistically significant.
Autor and Duggan (2003) used state-level difference equations to look at the effect of labor market conditions on DI applications. They found that state employment contractions were associated with increased DI applications. Their results were generally robust to fixed effects and other alternative specifications. Duggan and Imberman (2008) estimated annual time-series regressions of DI applications, awards, and recipients at the national level using more recent data (1984–2003) than previous studies. They produced results comparable with previous estimates reported by Rupp and Stapleton (1995); Black, Daniel, and Sanders (2002); and Autor and Duggan (2003). Duggan and Imberman's results showed that adverse labor market conditions have had significant effects on DI entry in the expected direction.
Soss and Keiser (2006) used a pooled cross-section analysis of both DI and SSI applications in a "seemingly unrelated regressions" framework. Their state-level models explained well over half of the variation in DI application rates and even more of the variation in SSI application rates. They found that increases in the state unemployment rate were associated with increases in both DI and SSI applications. Guo and Burton (2008, 2012) focused on state-level models of DI application rates with and without fixed effects and found that both specifications resulted in a substantial positive relationship between the unemployment rate and DI application rates. Using state-level data for the 1993–2009 period, Coe and others (2011) investigated the extent to which state-level variation in DI application rates reflected differences in health, demographic and employment characteristics of the population, policies, and politics. The authors presented estimates with and without state fixed effects. The models not including state fixed effects explained 70–80 percent of the state-level variation in application rates depending on specification and program group, whereas the models with fixed effects explained 85–93 percent of the variation. All three fixed-effects models estimated a positive unemployment rate coefficient, but only two of them (overall DI and DI/SSI concurrent) were statistically significant.
Thus, recent studies generally found a positive relationship between labor market shocks and disability applications. They used a variety of methodologies and their point estimates varied and were not always directly comparable, but the qualitative conclusion of a positive association was consistent across studies. Only two studies (Rupp and Stapleton (1995) and Strand (2002)) provided direct estimates of the relationship between the unemployment rate and disability allowance rates.6 Both considered a number of state-level variables and provided evidence consistent with the hypothesis of a negative link.
Data and Methodology
In this study, I build on previous work that used fixed-effects modeling to assess factors affecting disability applications, allowances, and the allowance rate. My initial disability determination model is as follows:
Yist = α + βXist + γUEst+ δs + ζt + εist,
where
Yist = initial decision for individual i, in state s in year t (ist) − Yist = 1 if initial decision is an allowance, Yist = 0 if initial decision is a denial;
Xist = vector of characteristics for individual (ist) subject to the initial determination;
UEst = the state unemployment rate for state (s) at year (t);
α = estimated intercept;
β = vector of estimated coefficients for individual characteristics;
γ = estimated coefficient for the unemployment rate;
δs= estimated fixed effect for state (s);
ζt = estimated fixed effect for year (t); and
εist = a random error term.
In the individual-level models, I use a logit specification with the result of the initial disability determination (1 = allowance, 0 = denial) as the dependent variable. All models include state and time fixed effects. Additional independent variables include the natural logarithm of the state unemployment rate and individual indicators for sex (female = 1); age group (dummies for the following age groups for adults: 18–24, 25–29, 30–34, 35–39, 40–44, 45–49, 50–54, 55–59, 60–64, with 50–54 chosen as the reference group and dummies for the following age groups for children: 0–5, 6–12, 13–17, with 0–5 chosen as the reference group); primary diagnosis (15 dummies, with musculoskeletal chosen as the reference group7); and the presence of a secondary diagnosis indicator8 (yes = 1). While this study improves on previous work partly by including those individual-level variables that provide substantial controls for factors affecting allowance rates, there are unobserved aspects of case severity that are not explicitly accounted for in the econometric model. Program group is a stratifying variable (DI-only adult, SSI-only adult, concurrent adult, SSI child). All of the states and the District of Columbia are included as "states"; Puerto Rico and the US territories are excluded from the sample frame.
I also conduct additional analyses using state-level data to address issues related to the possibility of aggregation bias that may have affected previous studies, to assess the predictive properties of my models, and to address issues related to variation in allowance rates across space and time. Most of my state-level models use OLS as did related work by Strand (2002). In addition, I explore issues related to possible lagged effects using generalized least squares (GLS) to correct for autocorrelation.9
There are several innovative features of the present study. This is the first study that controls for the demographic and diagnostic mix of individual applicants—two sets of variables known to be strongly related to the probability of an initial allowance. Their inclusion allows me to analyze the role of the unemployment rate controlling for and conditional on the characteristics of applicants. The data cover a longer and more recent period than did previous studies. Finally, previous studies did not separately estimate models for SSI childhood allowance rates, while this study does.
The study universe consists of 1,736,554 records, a 5 percent random sample of initial determinations for the 1993–2008 period. The sample frame includes DI-only adults, SSI-only adults, concurrent adults, and SSI childhood initial determinations. The sample frame excludes DI-only and concurrent childhood initial determinations (consisting of 1,698 observations, or about 0.1 percent of the source 5 percent sample). The data source is the so-called "831 file"10 from SSA's National Disability Determination Services System File, which contains data on DDS initial determinations. As previously noted, technical denials made by SSA prior to sending application records to the DDS are not included in the sample frame. The state unemployment rate for the given year, obtained from Current Population Survey data, was added to each initial determination record. Table 1 describes the characteristics of the applicant sample by SSA program group.
| Variable | Adult program group | SSI child | ||||||
|---|---|---|---|---|---|---|---|---|
| DI-only | SSI-only | Concurrent | ||||||
| Mean | Standard error | Mean | Standard error | Mean | Standard error | Mean | Standard error | |
| Number of observations | 484,591 | 426,141 | 520,538 | 305,284 | ||||
| Sex | ||||||||
| Proportion female | 0.480 | 0.001 | 0.550 | 0.001 | 0.462 | 0.001 | 0.373 | 0.001 |
| Age group (distribution) | ||||||||
| 0–5 | . . . | . . . | . . . | . . . | . . . | . . . | 0.376 | 0.001 |
| 6–12 | . . . | . . . | . . . | . . . | . . . | . . . | 0.434 | 0.001 |
| 13–17 | . . . | . . . | . . . | . . . | . . . | . . . | 0.190 | 0.001 |
| 18–24 | 0.013 | 0.000 | 0.177 | 0.001 | 0.087 | 0.000 | . . . | . . . |
| 25–29 | 0.026 | 0.000 | 0.078 | 0.000 | 0.090 | 0.000 | . . . | . . . |
| 30–34 | 0.046 | 0.000 | 0.097 | 0.000 | 0.104 | 0.000 | . . . | . . . |
| 35–39 | 0.074 | 0.000 | 0.119 | 0.000 | 0.127 | 0.000 | . . . | . . . |
| 40–44 | 0.107 | 0.000 | 0.133 | 0.001 | 0.143 | 0.000 | . . . | . . . |
| 45–49 | 0.140 | 0.000 | 0.132 | 0.001 | 0.145 | 0.000 | . . . | . . . |
| 50–54 | 0.182 | 0.001 | 0.113 | 0.000 | 0.138 | 0.000 | . . . | . . . |
| 55–59 | 0.217 | 0.001 | 0.087 | 0.000 | 0.113 | 0.000 | . . . | . . . |
| 60–64 | 0.196 | 0.001 | 0.064 | 0.000 | 0.054 | 0.000 | . . . | . . . |
| SSA primary diagnosis (distribution) | ||||||||
| Infectious and parasitic | 0.011 | 0.000 | 0.028 | 0.000 | 0.024 | 0.000 | 0.002 | 0.000 |
| Neoplasms | 0.095 | 0.000 | 0.027 | 0.000 | 0.045 | 0.000 | 0.009 | 0.000 |
| Endocrine | 0.040 | 0.000 | 0.052 | 0.000 | 0.052 | 0.000 | 0.013 | 0.000 |
| Blood | 0.003 | 0.000 | 0.004 | 0.000 | 0.003 | 0.000 | 0.011 | 0.000 |
| Mental a | 0.135 | 0.000 | 0.284 | 0.001 | 0.237 | 0.001 | 0.453 | 0.001 |
| Intellectual disability b | 0.007 | 0.000 | 0.056 | 0.000 | 0.020 | 0.000 | 0.110 | 0.001 |
| Musculoskeletal | 0.320 | 0.001 | 0.169 | 0.001 | 0.232 | 0.001 | 0.014 | 0.000 |
| Nervous | 0.079 | 0.000 | 0.069 | 0.000 | 0.067 | 0.000 | 0.072 | 0.000 |
| Circulatory | 0.112 | 0.000 | 0.076 | 0.000 | 0.091 | 0.000 | 0.008 | 0.000 |
| Respiratory | 0.039 | 0.000 | 0.040 | 0.000 | 0.037 | 0.000 | 0.101 | 0.001 |
| Digestive | 0.021 | 0.000 | 0.023 | 0.000 | 0.026 | 0.000 | 0.007 | 0.000 |
| Genitourinary | 0.015 | 0.000 | 0.011 | 0.000 | 0.013 | 0.000 | 0.005 | 0.000 |
| Skin | 0.002 | 0.000 | 0.003 | 0.000 | 0.003 | 0.000 | 0.003 | 0.000 |
| Congenital | 0.001 | 0.000 | 0.003 | 0.000 | 0.001 | 0.000 | 0.029 | 0.000 |
| Other primary | 0.002 | 0.000 | 0.001 | 0.000 | 0.002 | 0.000 | 0.069 | 0.000 |
| Unknown | 0.059 | 0.000 | 0.098 | 0.000 | 0.077 | 0.000 | 0.084 | 0.001 |
| Missing | 0.057 | 0.000 | 0.057 | 0.000 | 0.069 | 0.000 | 0.009 | 0.000 |
| SSA secondary impairment | ||||||||
| Proportion yes | 0.528 | 0.001 | 0.511 | 0.001 | 0.543 | 0.001 | 0.381 | 0.001 |
| Unemployment rate | 5.296 | 0.002 | 5.481 | 0.002 | 5.337 | 0.002 | 5.366 | 0.002 |
| Allowance rate | 0.437 | 0.001 | 0.314 | 0.001 | 0.287 | 0.001 | 0.396 | 0.001 |
| SOURCES: Data are based on 1,736,554 initial disability determinations in the 50 states and the District of Columbia for the 1993–2008 period, taken from SSA's National Disability Determination Services System File. State unemployment rate data are taken from the Current Population Survey. | ||||||||
| NOTES: Study universe is a 5 percent random sample of all initial determinations in the United States during the period under study. Technical denials made by SSA prior to sending the application records to the DDSs (reflecting decisions concerning ineligibility of the applicant based on nondisability criteria) are not included in the sample frame. The state unemployment rate for the applicable year was added to each initial determination record. | ||||||||
| . . . = not applicable. | ||||||||
| a. Not including intellectual disability. | ||||||||
| b. Intellectual disability was formerly known as mental retardation. | ||||||||
Results
This section is organized around two topics: (1) estimated effects of demographic characteristics, diagnostic factors, and the unemployment rate on the initial allowance rate; and (2) differences in allowance rates among the states.
Estimated Effects of Demographic and Diagnostic Factors and the Unemployment Rate on the Initial Allowance Rate
Table 2 shows the estimated effect of demographic characteristics, diagnostic factors, and the state unemployment rate on the probability of an initial allowance from fixed-effects logit regressions. The models in this table include state and year fixed effects, as well as the following time-varying factors: demographic characteristics, primary diagnosis, the presence of a secondary diagnosis, and the state unemployment rate. The results show that both sex and age are associated with the probability of an initial allowance. Women have a lower probability of an allowance for all program groups. The positive relationship between age and the probability of an initial allowance is strong and remarkably similar across the three adult program groups.11 Children aged 0–5 are more likely to be allowed than those aged 6–17.
| Parameter | Adult program group | SSI child | ||
|---|---|---|---|---|
| DI-only | SSI-only | Concurrent | ||
| Intercept | 0.385*** | -0.163*** | -0.034 | 0.032 |
| Sex | ||||
| Female | -0.292*** | -0.125*** | -0.177*** | -0.175*** |
| Male (reference group) | . . . | . . . | . . . | . . . |
| Age group | ||||
| 0–5 (reference group) | . . . | . . . | . . . | . . . |
| 6–12 | . . . | . . . | . . . | -0.962*** |
| 13–17 | . . . | . . . | . . . | -0.832*** |
| 18–24 | -0.258*** | -0.513*** | -0.823*** | . . . |
| 25–29 | -0.617*** | -0.915*** | -0.825*** | . . . |
| 30–34 | -0.628*** | -0.828*** | -0.777*** | . . . |
| 35–39 | -0.625*** | -0.777*** | -0.734*** | . . . |
| 40–44 | -0.588*** | -0.684*** | -0.650*** | . . . |
| 45–49 | -0.478*** | -0.566*** | -0.538*** | . . . |
| 50–54 (reference group) | . . . | . . . | . . . | . . . |
| 55–59 | 0.722*** | 1.031*** | 0.808*** | . . . |
| 60–64 | 0.891*** | 1.253*** | 1.044*** | . . . |
| SSA primary diagnosis | ||||
| Infectious and parasitic | 1.905*** | 1.275*** | 2.030*** | 0.849*** |
| Neoplasms | 2.443*** | 2.228*** | 2.583*** | 3.250*** |
| Endocrine | 0.318*** | 0.361*** | 0.459*** | -0.064 |
| Blood | 1.224*** | 0.865*** | 1.376*** | 0.538*** |
| Mental a | 1.300*** | 1.401*** | 1.476*** | 0.960*** |
| Intellectual disability b | 2.840*** | 2.837*** | 2.607*** | 2.900*** |
| Musculoskeletal (reference group) | . . . | . . . | . . . | . . . |
| Nervous | 1.116*** | 1.050*** | 1.045*** | 0.920*** |
| Circulatory | 0.705*** | 0.655*** | 0.946*** | 0.358*** |
| Respiratory | 1.158*** | 0.548*** | 1.060*** | -1.079*** |
| Digestive | 0.546*** | 0.529*** | 0.811*** | 0.427*** |
| Genitourinary | 2.540*** | 2.282*** | 2.863*** | 0.223** |
| Skin | 0.227*** | 0.026 | 0.401*** | -0.615*** |
| Congenital | 0.963*** | 2.116*** | 0.917*** | 1.617*** |
| Other primary | 0.135* | 1.371*** | 0.761*** | 2.305*** |
| Unknown | -0.980*** | -1.586*** | -1.008*** | -0.370*** |
| Missing | 0.133*** | 0.148*** | 0.163*** | 0.481*** |
| SSA secondary impairment | ||||
| No (reference group) | . . . | . . . | . . . | . . . |
| Yes | -0.060*** | -0.040*** | -0.070*** | 0.363*** |
| Unemployment rate | -0.148*** | -0.133*** | -0.164*** | -0.094*** |
| Number of observations | 484,591 | 426,141 | 520,538 | 305,284 |
| Likelihood ratio χ2 | c 115,382 | c 91,089 | c 99,789 | c 80,713 |
| Probability > χ2 | <.0001 | <.0001 | <.0001 | <.0001 |
| Max-rescaled R2 | 0.284 | 0.270 | 0.250 | 0.314 |
| - 2 log likelihood, intercept only | 663,996 | 530,173 | 624,496 | 409,891 |
| - 2 log likelihood, intercept and covariates | 548,614 | 439,084 | 524,707 | 329,177 |
| SOURCES: Data are based on 1,736,554 initial disability determinations in the 50 states and the District of Columbia for the 1993–2008 period, taken from SSA's National Disability Determination Services System File. State unemployment rate data are taken from the Current Population Survey. | ||||
| NOTES: Study universe is a 5 percent random sample of all initial determinations in the United States during the period under study. Technical denials made by SSA prior to sending the application records to the DDSs (reflecting decisions concerning ineligibility of the applicant based on nondisability criteria) are not included in the sample frame. The state unemployment rate for the applicable year was added to each initial determination record. All models include state and year fixed effects; coefficients for those variables are not shown in the table. | ||||
| * = statistically significant—different from zero at the 0.95 level of confidence; ** = statistically significant—different from zero at the 0.99 level of confidence; *** = statistically significant—different from zero at the 0.999 level of confidence. |
||||
| . . . = not applicable. | ||||
| a. Not including intellectual disability. | ||||
| b. Intellectual disability was formerly known as mental retardation. | ||||
| c. Likelihood ratio χ2 degrees of freedom is 92 in the three adult models. It is 86 in the SSI child model. | ||||
There is substantial variation in the estimated marginal effect of primary diagnosis (Chart 1). Looking at DI-only adults, I observe that (net of the effect of other independent variables) having a musculoskeletal impairment (the reference category) is associated with a predicted probability of initial allowance that is the lowest of all primary impairment categories (except "unknown"). In contrast, having an intellectual disability, a disease of the genitourinary system, or neoplasms as a primary impairment substantially increases the probability of an initial allowance. The overall patterns are quite similar for SSI-only adults and concurrent adults. Remarkably, with a few exceptions, the patterns of estimated primary diagnosis effects are similar for SSI children. Having a secondary diagnosis has a relatively small estimated negative effect on the three adult program groups, while the coefficient for SSI childhood initial allowances is positive and significant.
Estimated marginal difference (evaluated at the mean) between the probability of allowance for applicants with an SSA primary diagnosis, compared with the reference group of applicants with a musculoskeletal disease as the primary diagnosis
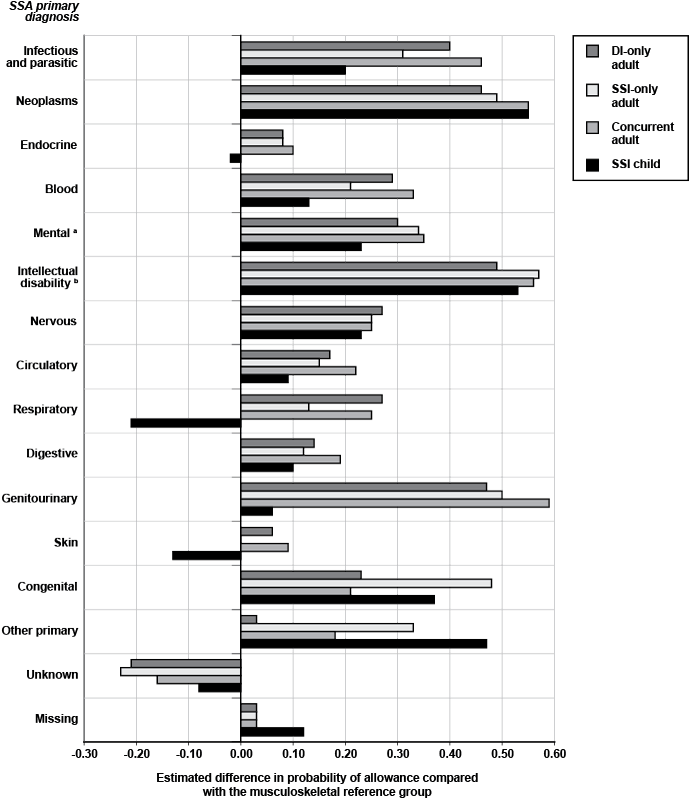
| SSA primary diagnosis | Adult group | SSI child | ||
|---|---|---|---|---|
| DI-only | SSI-only | Concurrent | ||
| Infectious and parasitic | 0.40 | 0.31 | 0.46 | 0.20 |
| Neoplasms | 0.46 | 0.49 | 0.55 | 0.55 |
| Endocrine | 0.08 | 0.08 | 0.10 | -0.02 |
| Blood | 0.29 | 0.21 | 0.33 | 0.13 |
| Mental a | 0.30 | 0.34 | 0.35 | 0.23 |
| Intellectual disability b | 0.49 | 0.57 | 0.56 | 0.53 |
| Nervous | 0.27 | 0.25 | 0.25 | 0.23 |
| Circulatory | 0.17 | 0.15 | 0.22 | 0.09 |
| Respiratory | 0.27 | 0.13 | 0.25 | -0.21 |
| Digestive | 0.14 | 0.12 | 0.19 | 0.10 |
| Genitourinary | 0.47 | 0.50 | 0.59 | 0.06 |
| Skin | 0.06 | 0.00 | 0.09 | -0.13 |
| Congenital | 0.23 | 0.48 | 0.21 | 0.37 |
| Other primary | 0.03 | 0.33 | 0.18 | 0.47 |
| Unknown | -0.21 | -0.23 | -0.16 | -0.08 |
| Missing | 0.03 | 0.03 | 0.03 | 0.12 |
Controlling for demographic and diagnostic characteristics of applicants, Table 2 also shows that an increase in the unemployment rate is associated with a decrease in the probability of an allowance for all four program groups. Table 3 explores that relationship further by comparing estimates of the unemployment rate coefficient from three different model specifications, by SSA program group. We start with a model that includes state and year fixed effects and the unemployment rate and then add demographic and diagnosis predictors in a sequential fashion to investigate the sensitivity of the unemployment rate coefficient. Model 1 includes state and year fixed effects and the unemployment rate as independent variables. Model 2 adds demographic predictors, while model 3 adds primary diagnosis variables and an indicator for the presence or absence of a secondary impairment. The top panel of Table 3 provides the results for the DI-only group. All three estimated coefficients are negative and statistically significant. The results are remarkably robust to model specification. The patterns are similar for SSI-only and concurrent adults. Notably, the estimated relationships for SSI children are quite similar to the results for adults, albeit the point estimates tend to be somewhat lower. The statistically significant negative relationship for children is remarkable because, unlike for adults, the reference person with a disability (the child) is not directly affected by the unemployment rate, and the person who may be affected by it (the adult parent) is not necessarily disabled. Thus, some of the explanations related to the effect of changes in the local unemployment rate on the employment status of the disabled applicant are not relevant in the same way as they may be for adults with disabilities. Plausible explanations involve the effect of job loss of adults on the financial eligibility of the child and the effect of adverse labor market conditions on the opportunity costs of disability application on behalf of the child. Chart 2 presents the corresponding estimates of marginal effects of the unemployment rate evaluated at the mean for each of the four SSA program groups.
| Model | Unemployment rate logit coefficient | N |
|---|---|---|
| DI-only adult | ||
| 1 | -0.123*** | 484,591 |
| 2 | -0.131*** | 484,591 |
| 3 | -0.148*** | 484,591 |
| SSI-only adult | ||
| 1 | -0.126*** | 426,141 |
| 2 | -0.142*** | 426,141 |
| 3 | -0.133*** | 426,141 |
| Concurrent adult | ||
| 1 | -0.146*** | 520,538 |
| 2 | -0.152*** | 520,538 |
| 3 | -0.164*** | 520,538 |
| SSI child | ||
| 1 | -0.100*** | 305,284 |
| 2 | -0.101*** | 305,284 |
| 3 | -0.094*** | 305,284 |
| SOURCES: Data are based on 1,736,554 initial disability determinations in the 50 states and the District of Columbia for the 1993–2008 period, taken from SSA's National Disability Determination Services System File. State unemployment rate data are taken from the Current Population Survey. | ||
| NOTES: Study universe is a 5 percent random sample of all initial determinations in the United States during the period under study. Technical denials made by SSA prior to sending the application records to the DDSs (reflecting decisions concerning ineligibility of the applicant based on nondisability criteria) are not included in the sample frame. The state unemployment rate for the applicable year was added to each initial determination record. | ||
| Predictors for models 1–3 are as follows: Model 1—year, state, and unemployment rate. Model 2—year, state, unemployment rate, and demographic characteristics of applicants. Model 3—year, state, unemployment rate, and demographic and diagnostic characteristics of applicants. |
||
| * = statistically significant—different from zero at the 0.95 level of confidence; ** = statistically significant—different from zero at the 0.99 level of confidence; *** = statistically significant—different from zero at the 0.999 level of confidence. |
||
Estimated effect of a 1 percentage point increase in the state unemployment rate on the probability of allowance (evaluated at the mean), by SSA program group and model specification
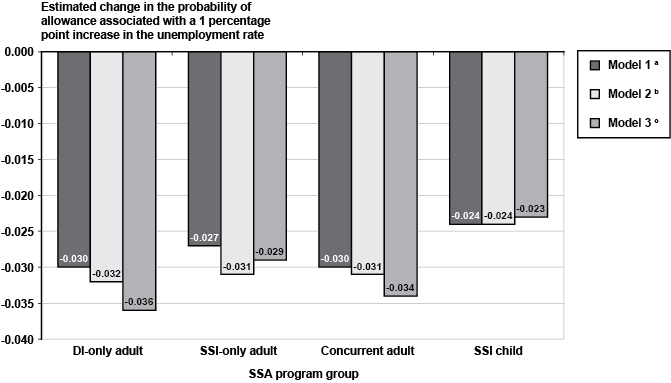
| Model | Adult group | SSI child | ||
|---|---|---|---|---|
| DI-only | SSI-only | Concurrent | ||
| 1 | -0.030 | -0.027 | -0.030 | -0.024 |
| 2 | -0.032 | -0.031 | -0.031 | -0.024 |
| 3 | -0.036 | -0.029 | -0.034 | -0.023 |
Given the wide variation in the marginal association between allowance outcomes and diagnostic categories (as shown in Table 2) for all four program groups, a more detailed analysis of the relationship between diagnosis and labor market shocks is warranted. Specifically, an important question is whether the unemployment rate effect is conditional on the diagnostic category of the applicant. Table 4 explores that possibility by presenting the estimated unemployment rate coefficients from separate logit models for each primary diagnosis group by SSA program group (68 regressions). Chart 3 shows only the estimated effects that are statistically significant—different from zero at least at the 0.95 level of confidence. All of the statistically significant coefficients are negative as expected.12 There is some variation among the diagnostic categories, suggesting that the unemployment rate has different effects on the allowance rate for different types of impairments. In particular, the estimated negative effect of the unemployment rate is consistently large across adult program groups for mental and musculoskeletal disorders. Importantly, all of the statistically significant estimates for SSI children are also negative (as shown in Table 4), albeit only three coefficients are significant (intellectual disabilities, mental impairments, and endocrine disorders). Thus, the evidence is strong for a tendency of a negative association between allowance rates and unemployment rate effects conditional on diagnosis for both adults and children.
| SSA primary diagnosis a | Adult program group | SSI child | ||
|---|---|---|---|---|
| DI-only | SSI-only | Concurrent | ||
| Infectious and parasitic | -0.080 | -0.071 | -0.063 | -0.136 |
| Neoplasms | -0.082*** | -0.020 | -0.040 | -0.050 |
| Endocrine | -0.145*** | -0.204*** | -0.239*** | -0.158* |
| Blood | -0.032 | 0.040 | -0.120 | 0.013 |
| Mental b | -0.191*** | -0.178*** | -0.209*** | -0.127*** |
| Intellectual disability c | -0.239** | -0.089*** | -0.165*** | -0.189*** |
| Musculoskeletal | -0.195*** | -0.204*** | -0.189*** | -0.012 |
| Nervous | -0.105*** | -0.086*** | -0.126*** | -0.039 |
| Circulatory | -0.121*** | -0.188*** | -0.148*** | 0.080 |
| Respiratory | -0.083** | -0.073* | -0.148*** | -0.059 |
| Digestive | -0.093* | -0.087* | -0.184*** | 0.035 |
| Genitourinary | -0.129* | -0.019 | -0.048 | 0.027 |
| Skin | 0.069 | -0.102 | 0.038 | -0.256 |
| Congenital | -0.230 | -0.056 | -0.055 | -0.002 |
| Other | -0.127 | 0.061 | -0.376* | -0.047 |
| Unknown | -0.114*** | -0.006 | -0.045 | 0.045 |
| Missing | -0.152*** | -0.089** | -0.163*** | -0.088 |
| SOURCES: Data are based on 1,736,554 initial disability determinations in the 50 states and the District of Columbia for the 1993–2008 period, taken from SSA's National Disability Determination Services System File. State unemployment rate data are taken from the Current Population Survey. | ||||
| NOTES: Study universe is a 5 percent random sample of all initial determinations in the United States during the period under study. Technical denials made by SSA prior to sending the application records to the DDSs (reflecting decisions concerning ineligibility of the applicant based on nondisability criteria) are not included in the sample frame. The state unemployment rate for the applicable year was added to each initial determination record. | ||||
| * = statistically significant—different from zero at the 0.95 level of confidence; ** = statistically significant—different from zero at the 0.99 level of confidence; *** = statistically significant—different from zero at the 0.999 level of confidence. |
||||
| a. Regression models are conditioned on the presence of the SSA primary diagnosis category. The estimates are also disaggregated by program group. Numeric entries and significance levels in the table represent results from 68 separate regressions. | ||||
| b. Not including intellectual disability. | ||||
| c. Intellectual disability was formerly known as mental retardation. | ||||
Estimated effect of a 1 percentage point increase in the state unemployment rate on the probability of allowance, by SSA primary diagnosis
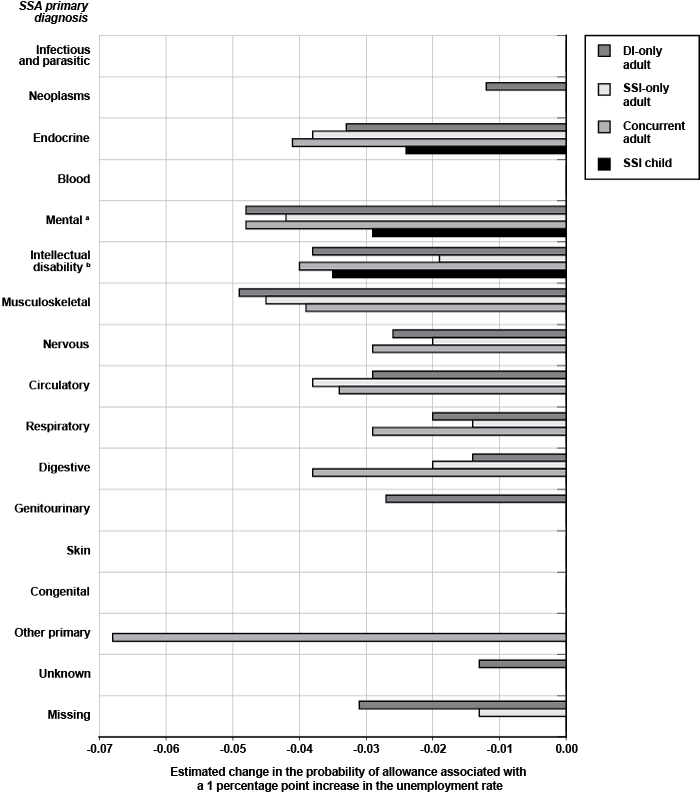
| SSA primary diagnosis | Adult group | SSI child | ||
|---|---|---|---|---|
| DI-only | SSI-only | Concurrent | ||
| Infectious and parasitic | 0.000 | 0.000 | 0.000 | 0.000 |
| Neoplasms | -0.012 | 0.000 | 0.000 | 0.000 |
| Endocrine | -0.033 | -0.038 | -0.041 | -0.024 |
| Blood | 0.000 | 0.000 | 0.000 | 0.000 |
| Mental a | -0.048 | -0.042 | -0.048 | -0.029 |
| Intellectual disability b | -0.038 | -0.019 | -0.040 | -0.035 |
| Musculoskeletal | -0.049 | -0.045 | -0.039 | 0.000 |
| Nervous | -0.026 | -0.020 | -0.029 | 0.000 |
| Circulatory | -0.029 | -0.038 | -0.034 | 0.000 |
| Respiratory | -0.020 | -0.014 | -0.029 | 0.000 |
| Digestive | -0.014 | -0.020 | -0.038 | 0.000 |
| Genitourinary | -0.027 | 0.000 | 0.000 | 0.000 |
| Skin | 0.000 | 0.000 | 0.000 | 0.000 |
| Congenital | 0.000 | 0.000 | 0.000 | 0.000 |
| Other primary | 0.000 | 0.000 | -0.068 | 0.000 |
| Unknown | -0.013 | 0.000 | 0.000 | 0.000 |
| Missing | -0.031 | -0.013 | 0.000 | 0.000 |
Generally, increases in the unemployment rate are associated with reductions in the probability of an initial allowance outcome—a finding that is fairly robust. This is consistent with the hypothesis that deteriorating labor market conditions have a positive effect on applications13 through drawing in marginally qualified applicants and that SSA is successful in screening out many of those marginally qualified applicants in the initial determination phase.
Because previous related studies used state-level data, it is worthwhile to compare results from this study with those of studies employing similar models; I use a data set aggregated to the state level. The state-level results are summarized in Table 5, where I use the same underlying data set that was used for the individual-level analysis to facilitate comparability with that analysis. Table 5 shows that the state-level estimates of the effect of the unemployment rate on allowance rates are robust to weighting and model specification. The dependent variable in all of the models is the initial allowance rate. Models 1–5 use independent variables that are directly comparable to the individual-level predictors. All of the estimated effects are statistically significant and negative; they vary in a relatively narrow range and are similar to the estimated marginal effects from the individual-level models.
| Model | Adult program group | SSI child | ||
|---|---|---|---|---|
| DI-only | SSI-only | Concurrent | ||
| Estimated effect of a 1 percentage point increase in the unemployment rate on the allowance rate | ||||
| 1 | -0.025*** | -0.026*** | -0.024*** | -0.024*** |
| 2 | -0.026*** | -0.029*** | -0.022*** | -0.024*** |
| 3 | -0.023*** | -0.023*** | -0.022*** | -0.021*** |
| 4 | -0.023*** | -0.025*** | -0.021*** | -0.021*** |
| 5 | -0.026*** | -0.016*** | -0.022*** | -0.016*** |
| 6: set 1 | -0.025*** | -0.024*** | -0.020*** | -0.023*** |
| Estimated effect of a 1 percent increase in the number of initial determinations on the allowance rate | ||||
| 6: set 2 | -0.027 | -0.054*** | -0.049** | -0.003 |
| SOURCES: Data are based on 1,736,554 initial disability determinations in the 50 states and the District of Columbia for the 1993–2008 period, taken from SSA's National Disability Determination Services System File. State unemployment rate data are taken from the Current Population Survey. | ||||
| NOTES: Study universe is a 5 percent random sample of all initial determinations in the United States during the period under study. Technical denials made by SSA prior to sending the application records to the DDSs (reflecting decisions concerning ineligibility of the applicant based on nondisability criteria) are not included in the sample frame. The state unemployment rate for the applicable year was added to each initial determination record. | ||||
| The dependent variable in all of the models is the initial allowance rate, expressed as a fraction. Independent variables for models 1–6 are as follows: Model 1—year, state, and unemployment rate (unweighted). Model 2—year, state, unemployment rate, and demographic characteristics of applicants (unweighted). Model 3—year, state, unemployment rate, and diagnostic characteristics of applicants (unweighted). Model 4—year, state, unemployment rate, and demographic and diagnostic characteristics of applicants (unweighted). Model 5—year, state, unemployment rate, and demographic and diagnostic characteristics of applicants (weighted). Model 6 (sets 1 and 2)—year, state, unemployment rate, and natural logarithm of number of initial determinations (unweighted). |
||||
| * = statistically significant—different from zero at the 0.95 level of confidence; ** = statistically significant—different from zero at the 0.99 level of confidence; *** = statistically significant—different from zero at the 0.999 level of confidence. |
||||
An additional issue I address is the three-way relationship between the unemployment rate, volume of applications, and initial allowance rate. From previous research, we know that there is strong evidence of a positive relationship between the unemployment rate and the number of initial applications; as the unemployment rate increases, more people apply for disability benefits. One question that comes to mind is whether the negative association between the unemployment rate and initial allowance rate is simply a reflection of that increased volume or whether the association continues to be negative and statistically significant after controlling for the volume of applications. A related question is whether increases in the volume of applications are associated with the initial allowance rate for reasons unrelated to increases in the unemployment rate. In order to answer these questions, both the unemployment rate and the volume of applications need to be included as independent variables in the regression model. Model 6 includes both variables, using the natural logarithm of the number of initial determinations in the state as the indicator of the volume of applications (see Table 5). Two sets of estimated coefficients (sets 1 and 2) are provided for model 6 to answer the two questions above. The first set shows the unemployment rate coefficient for the four program groups and the second set displays the initial determinations coefficients. The estimated unemployment rate effects are highly robust to the inclusion or exclusion of the initial determinations independent variable, suggesting that the relationship between the unemployment rate and initial allowance rates is not explained by the increased volume of applications associated with higher unemployment. Having said that, the volume of applications also has an independent effect. All four estimated coefficients are negative, suggestive of an independent negative relationship between changes in the number of initial determinations and changes in the initial allowance rate, although only two of these coefficients are statistically significant.
Finally, I conduct tests addressing the temporal dimension of the relationship between the unemployment rate and initial allowance rates. Recall that Rupp and Stapleton (1995) reported statistically significant negative lagged effects from state-level models, but no significant relationship between the unemployment rate and initial allowance rates for the same year. In contrast, both my individual- and state-level analyses show statistically significant negative relationships for the same year. Consequently, I conduct further analysis of my state-level data to shed light on the source of those differences. Similar to Rupp and Stapleton (1995), I use models that correct for autocorrelation and include lagged values of the unemployment rate predictor.
In Table 6, correcting for autocorrelation using generalized least squares (GLS) without including lagged values of the unemployment rate predictor does not affect the sign and statistical significance of the adult current-year unemployment rate coefficients, but produces coefficients that are smaller in absolute value. For childhood models using the current-year unemployment rate predictor, the GLS estimate is not statistically significantly different from zero in two of the models, but is statistically significant and positive in the model that controls for both demographic and diagnostic factors.
| Time period: Unemployment variable(s) | Adult program group | SSI child | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DI-only | SSI-only | Concurrent | ||||||||||
| t | t-1 | t-2 | t | t-1 | t-2 | t | t-1 | t-2 | t | t-1 | t-2 | |
| Model 1 | ||||||||||||
| t | -0.016*** | . . . | . . . | -0.011*** | . . . | . . . | -0.007*** | . . . | . . . | 0.000 | . . . | . . . |
| t, t-1 | -0.001 | -0.016*** | . . . | -0.004 | -0.007 | . . . | -0.006 | -0.001 | . . . | 0.013 | -0.014* | . . . |
| t, t-1, t-2 | -0.006 | 0.002 | -0.014*** | -0.009 | 0.010 | -0.014** | -0.007 | 0.003 | -0.003 | 0.002 | 0.026* | -0.032*** |
| Model 2 | ||||||||||||
| t | -0.015*** | . . . | . . . | -0.013*** | . . . | . . . | -0.008*** | . . . | . . . | 0.000 | . . . | . . . |
| t, t-1 | 0.002 | -0.019*** | . . . | -0.013** | 0.000 | . . . | -0.005 | -0.003 | . . . | 0.013* | -0.140* | . . . |
| t, t-1, t-2 | -0.003 | -0.001 | -0.015** | -0.017*** | 0.016* | -0.013* | -0.007 | 0.004 | -0.006 | 0.001 | 0.028** | -0.034*** |
| Model 3 | ||||||||||||
| t | -0.009*** | . . . | . . . | -0.011*** | . . . | . . . | -0.008*** | . . . | . . . | 0.01*** | . . . | . . . |
| t, t-1 | -0.001 | -0.009* | . . . | -0.0135*** | 0.002 | . . . | -0.004 | -0.004 | . . . | 0.014 | -0.005 | . . . |
| t, t-1, t-2 | -0.005 | 0.004 | -0.011** | -0.018*** | 0.018** | -0.013** | -0.006 | -0.004 | -0.007* | 0.007 | 0.019* | -0.021*** |
| SOURCES: Data are based on 1,736,554 initial disability determinations in the 50 states and the District of Columbia for the 1993–2008 period, taken from SSA's National Disability Determination Services System File. State unemployment rate data are taken from the Current Population Survey. | ||||||||||||
| NOTES: Study universe is a 5 percent random sample of all initial determinations in the United States during the period under study. Technical denials made by SSA prior to sending the application records to the DDSs (reflecting decisions concerning ineligibility of the applicant based on nondisability criteria) are not included in the sample frame. The state unemployment rate for the applicable year was added to each initial determination record. | ||||||||||||
| Lagged unemployment rate predictors follow: t = current year; t-1 = 1 year earlier; t-2 = 2 years earlier. | ||||||||||||
| The dependent variable for all of the models is the initial allowance rate, expressed as a fraction. | ||||||||||||
| Independent variables for models 1–3 are as follows: Model 1—year, state, and unemployment rate. Model 2—year, state, unemployment rate, and demographic characteristics of applicants. Model 3—year, state, unemployment rate, and demographic and diagnostic characteristics of applicants. |
||||||||||||
| * = statistically significant—different from zero at the 0.95 level of confidence; ** = statistically significant—different from zero at the 0.99 level of confidence; *** = statistically significant—different from zero at the 0.999 level of confidence. |
||||||||||||
Next, I look at the effect of including lagged values of the unemployment rate predictor. In most cases, the inclusion of lagged values did not change the sign of the current-year (period t) coefficient, but tended to eliminate statistical significance. Most strikingly, when both period t-1 and period t-2 lagged predictors are added, all of the t-2 coefficients are consistently negative and in most cases statistically significantly different from zero. I measure the cumulative effect by the sum of the three coefficients and estimate it as -1.8 percent for DI-only adults, -1.3 percent for SSI-only adults, -0.7 percent for concurrent adults, and -0.8 percent for SSI children (author's calculation based on model 1 estimates in Table 6).
Based on this analysis, the current study and the Rupp and Stapleton (1995) estimates are consistent with respect to finding evidence to support the hypothesis of lagged effects of the unemployment rate on initial allowance rates, but inconsistent in that the 1995 study failed to show current-year effects. The inconsistency with respect to current-year effects may of course reflect the fact that the two studies are based on data reflecting very different time periods and economic conditions. In my view, however, there are reasons to have confidence in the current study's findings of current-year effects and to conclude that the failure of the 1995 study to find current-year effects may be attributable to data limitations of that study. With respect to this analysis, the current-year estimates are consistent and statistically significant using a large number of individual- and state-level models pertaining to a large number of subgroups. In addition, this study includes detailed controls for demographic variables and the diagnostic mix of applicants, while the previous study lacked this level of detail. Finally, the data for the 1995 study had some unique weaknesses, as discussed by Stapleton, Dietrich, and Lo (1995). The most important in this context is the fact that there was a temporal misalignment in that study between the data set pertaining to the unemployment rate and the administrative data on initial determinations that should bias current-year estimates toward zero. Specifically, while the unemployment rate data were compiled based on a calendar-year basis, the initial determination data reflected a fiscal-year concept that started 3 months earlier.
Several conclusions and issues for future research arise from the analysis presented in Table 6. The state-level estimates therein are generally consistent with the hypothesis of a negative relationship between disability allowance rates and the local unemployment rate. The evidence is strongest for DI and SSI adults and somewhat weaker for concurrent adults and SSI children. The analysis also suggests that both current-year and lagged unemployment rate effects are present, that is, the unemployment rate affects initial allowance rates during the same calendar year, but some of the effects on initial allowance rates materialize years later. The evidence of lagged effects on allowance rates is consistent with the finding of Burkhauser, Butler, and Weathers (2001/2002) that the risk of applying for DI benefits is highest during the year immediately after the onset of a work-limiting condition, but the median duration between onset and disability application is much longer. Because the issue of possible lagged effects of the unemployment rate and initial disability allowance rates has substantial policy relevance and, to my knowledge, is addressed only in this article and in Rupp and Stapleton (1995), more research on the temporal structure of the unemployment rate effect is warranted.
State-to-State Differences in Observed Allowance Rates
In this section, I address two additional aspects of state-to-state differences in allowance rates. The first explores prediction and the second deals with the understanding of variations of allowance rates across space and time. Neither aspect involves causal inference. The term "explanation"—commonly used in this context (for example, explanation of R2)—does not imply causation.
The issue of the predictive power of the regression models has to do with the ability of the independent variables included in the models to predict the allowance rate for individual states. In assessing the quality of the state-level predictions, following Strand (2002), I use the counterfactual of the average absolute difference between the state and national mean as the main measurement tool; in the absence of any additional information, the national mean is the best predictor of the state allowance rate. My model, however, considers a number of additional variables that allow me to calculate a predicted allowance rate for each state that itself varies around the national average. The expectation is that the average absolute difference between observed and predicted state allowance rates is smaller than the counterfactual that considers only the national average in the prediction. The magnitude of reduction is my key measure of the predictive ability of the model.
First, I look at the relationship between observed and model-predicted allowance rates by state and program group for selected years. Table 7 shows the average observed and model-predicted allowance rate for the states, the standard deviation of observed and predicted state allowance rates, the average absolute difference between the state and national mean, and the average absolute difference between the observed and predicted state average. All of the estimates are based on unweighted averages of the state-level statistics.
| Year | State allowance rate | Standard deviation of state allowance rates | Average absolute difference between— | Reduction of average absolute difference attributable to model | ||||
|---|---|---|---|---|---|---|---|---|
| Observed | Predicted | Observed | Predicted | State and national mean |
Observed and predicted state rate | Percentage point | Percent | |
| DI-only adult | ||||||||
| 1993 | 43.6 | 43.7 | 7.7 | 7.0 | 6.2 | 4.6 | -1.6 | -25.5 |
| 1995 | 40.9 | 39.5 | 8.1 | 6.6 | 6.3 | 4.8 | -1.5 | -23.7 |
| 2000 | 47.3 | 46.7 | 9.4 | 7.2 | 7.8 | 4.0 | -3.7 | -48.1 |
| 2005 | 45.9 | 45.7 | 8.8 | 7.0 | 6.9 | 3.5 | -3.4 | -49.0 |
| 2008 | 47.1 | 48.8 | 7.7 | 7.1 | 5.9 | 4.1 | -1.8 | -30.3 |
| SSI-only adult | ||||||||
| 1993 | 36.0 | 36.0 | 9.2 | 7.1 | 7.3 | 5.0 | -2.3 | -31.5 |
| 1995 | 29.4 | 28.4 | 6.7 | 5.7 | 5.0 | 4.3 | -0.8 | -15.7 |
| 2000 | 34.8 | 34.1 | 8.2 | 6.6 | 6.2 | 3.3 | -2.9 | -47.4 |
| 2005 | 32.9 | 33.1 | 10.4 | 8.0 | 8.0 | 3.6 | -4.4 | -54.8 |
| 2008 | 34.0 | 34.1 | 7.4 | 7.1 | 5.8 | 3.5 | -2.3 | -40.4 |
| Concurrent adult | ||||||||
| 1993 | 32.0 | 32.3 | 7.3 | 5.6 | 6.1 | 4.7 | -1.4 | -22.5 |
| 1995 | 27.5 | 26.9 | 6.3 | 4.9 | 4.4 | 3.8 | -0.6 | -14.2 |
| 2000 | 32.9 | 32.3 | 8.0 | 6.7 | 5.6 | 3.4 | -2.2 | -39.9 |
| 2005 | 29.3 | 28.7 | 8.9 | 6.9 | 6.9 | 3.1 | -3.8 | -55.3 |
| 2008 | 29.6 | 30.4 | 7.3 | 6.2 | 5.3 | 3.4 | -2.0 | -36.9 |
| SSI child | ||||||||
| 1993 | 50.4 | 52.4 | 8.1 | 7.5 | 6.2 | 5.6 | -0.6 | -9.9 |
| 1995 | 33.7 | 33.2 | 10.5 | 7.9 | 7.9 | 4.1 | -3.9 | -48.7 |
| 2000 | 43.9 | 44.0 | 10.6 | 9.3 | 8.0 | 4.2 | -3.8 | -47.5 |
| 2005 | 46.7 | 45.3 | 10.6 | 9.3 | 9.9 | 4.1 | -5.8 | -58.5 |
| 2008 | 45.6 | 45.1 | 12.6 | 10.6 | 10.0 | 4.3 | -5.8 | -57.6 |
| SOURCES: Data are based on 1,736,554 initial disability determinations in the 50 states and the District of Columbia for the 1993–2008 period, taken from SSA's National Disability Determination Services System File. State unemployment rate data are taken from the Current Population Survey. | ||||||||
| NOTES: Study universe is a 5 percent random sample of all initial determinations in the United States during the period under study. Technical denials made by SSA prior to sending the application records to the DDSs (reflecting decisions concerning ineligibility of the applicant based on nondisability criteria) are not included in the sample frame. The state unemployment rate for the applicable year was added to each initial determination record. | ||||||||
When I compare the average observed and predicted initial allowance rates for individual years, all of the differences are within 2 percentage points. Most are much smaller: 16 of the 20 estimates show a difference of 1 percentage point or less. The standard deviation of predicted state allowance rates is noticeably lower. An arguably better measure of the explanatory strength of the model is given by comparing the average absolute difference between the observed state and national mean (a model with no predictors) with the average absolute difference between the observed and model-predicted state averages. As in Strand (2002), I prefer the average absolute difference measure to the standard deviation measure because outliers unduly influence the standard deviation. The model results in substantial reduction. For example, for DI-only adults in the year 2000, state allowance rates on average varied 7.8 percentage points in either direction from the national average. The model accounts for 4.0 percentage points, explaining roughly half of the average absolute difference. In other words, the individual-level predictions aggregated to the state level reduce the average absolute difference in allowance rates by roughly half, as opposed to the counterfactual, which compares raw state allowance rates with the national average allowance rate. The magnitude of the results is comparable to Strand's results for DI and SSI allowance rates in 1999. The magnitude of the reduction in average absolute value of the difference between observed and predicted allowance rates is expressed both in percentage point and percent terms in the two columns with the heading "Reduction of average absolute difference attributable to model" (Table 7). The percent reduction varies by 10–59 percent, but most are substantial—9 of the 20 estimates are close to or above 50 percent.
Table 8 explores the sensitivity of predictive accuracy to the use of individual-level compared with state-level models14 and to decisions about the use of weights. It compares the results of five alternative methods to measure overall accuracy. In this analysis, weights are used in two distinct steps. The first is the estimation of the regression model. The individual-level models are "self-weighting," while the state-level models can be estimated unweighted or weighted. In this context, the term self-weighting means that (1) the individual-level models weight each initial determination equally, and (2) the result is that each state is represented proportionally to the number of initial determinations in that state.15 The second step is the derivation of summary statistics at the national level from the state-level estimates. The averaging is either unweighted (giving each state equal weight, regardless of size), or weighted (giving each state a weight proportional to the number of initial determinations in that state). I illustrate the sensitivity of results to the level of aggregation of the sample used for the regression model and weighting at two steps in the analysis based on calculations showing DI outcomes for the year 2000. Method 1 represents the kind of statistics the previous results in Table 5 were based on (individual-level logit model, self-weighting sample used for model estimation, and unweighted average of state-level results to derive the national average absolute difference). The findings from Table 8 are straightforward. First, the estimated average absolute difference between observed and model-predicted values is not sensitive to the use of individual-level versus state-level data in the modeling; there is only a 0.2 percentage point difference between the individual-level method 1 and the state-level method 3 results. The same is true in the comparison of method 2 and method 5. Second, the results are not sensitive to giving equal weight to each state or using weights proportional to the number of initial allowances in the state-level models; the result from method 4 is only 0.2 percentage points higher than the result from method 5. Third, the only factor that affects the magnitude of the average absolute difference in a meaningful way is the use of weighting in summarizing state-level averages to the national level. When state results are weighted by size (the number of initial determinations), there is a clear reduction in the average absolute difference compared with results that give equal weight to the states in summarizing the state-level results to the national level. The unweighted average of the state-level estimates from the individual-level model (method 1) is 4.0 percentage points, while the corresponding weighted average of the states from method 2 is 3.3 percentage points—a difference of 0.7 percentage points (a substantial percent reduction). The magnitude of difference between method 3 (unweighted state averages) and method 4 (weighted state averages) displays a similar pattern (0.5 percentage points). The reduction arising from weighting the state averages is partly explained by the fact that random error of state-level estimates is negatively related to size. That suggests that some of the unexplained variation in the unweighted state-level models is attributable to random variation; the weighted estimates give more weight to the larger states, while the unweighted estimates are unduly influenced by very small states, especially because the state-level estimates are based on an underlying 5 percent sample of individual-level observations rather than a larger sample.16
| Method | Level of analysis and estimation method a | Method of weighting | Estimated average absolute difference between observed and predicted state average allowance rates in percentage points | |
|---|---|---|---|---|
| Model | Summary statistics | |||
| 1 | Individual-level, logit | Self-weighting b | Unweighted average of states c | 4.0 |
| 2 | Individual-level, logit | Self-weighting b | Weighted state averages d | 3.3 |
| 3 | State-level, OLS | Unweighted e | Unweighted average of states c | 3.8 |
| 4 | State-level, OLS | Unweighted e | Weighted state averages d | 3.3 |
| 5 | State-level, OLS | Weighted f | Weighted state averages d | 3.1 |
| SOURCES: Data are based on 1,736,554 initial disability determinations in the 50 states and the District of Columbia for the 1993–2008 period, taken from SSA's National Disability Determination Services System File. State unemployment rate data are taken from the Current Population Survey. | ||||
| a. In estimating the individual-level regression model, the unit of observation is the individual initial determination; in state-level models, it is the state. | ||||
| b. Self-weighting means that each initial determination is weighted equally. As a result, each state is represented proportionally to size, that is, proportionally to the number of initial determinations. | ||||
| c. The calculation of the national average of states gives equal weight to each state, regardless of size. | ||||
| d. In the calculation of the national average, each state is represented proportionally to the number of initial determinations in that state. | ||||
| e. In estimating the regression model, each state receives equal weight, regardless of size. | ||||
| f. In estimating the regression model, each state receives a weight proportional to the number of initial determinations in that state. | ||||
Next, I consider how my fixed-effects models contribute to the understanding of the overall variation in allowance rates across states. The R2 is commonly used to assess the variation "explained" by the independent variables included in a regression model. This explanation is purely descriptive and does not reflect causal understanding. In the context of fixed-effects modeling, we can go a little further and decompose the total variation into the following four components:
- variation attributable to unmeasured factors that reflect long-term differences among the states,
- additional variation attributable to unmeasured factors that reflect year-specific national differences,
- additional variation attributable to the effect of specific independent variables that vary by state and over time, and
- unexplained variation that may result from unmeasured time-varying factors not explicitly considered in the model or from purely random fluctuations.
Table 9 shows the decomposition of total variation. State fixed effects reflect long-term differences among states and account for 41–52 percent of explained variation. Note that state fixed effects do not provide any specific information about the reasons for these long-term differences, which may be due to factors that are exogenous or endogenous to program management. Next, I find that year effects range widely by program group from 9 percent for concurrent adults to 29 percent for the SSI-child category. Year effects pick up the effects of changes over time that affect all states equally. Perhaps it is not surprising that the variation explained by year effects is by far the highest for the SSI-child program group, given the enormous volatility of national policies and their implementation from the Supreme Court's "Zebley" decision to the 1996 welfare reform. Note that state and time fixed effects combined explain 55–79 percent of the overall variation.17
| Component of variation a | Adult program group | SSI child | ||
|---|---|---|---|---|
| DI-only | SSI-only | Concurrent | ||
| State fixed effects | 52 | 41 | 46 | 50 |
| Year fixed effects | 14 | 16 | 9 | 29 |
| Time-varying independent variables (unemployment rate and demographic and diagnostic characteristics of applicants) | 10 | 17 | 18 | 6 |
| Unexplained b | 24 | 25 | 27 | 16 |
| Total | 100 | 100 | 100 | 100 |
| SOURCES: Data are based on 1,736,554 initial disability determinations in the 50 states and the District of Columbia for the 1993–2008 period, taken from SSA's National Disability Determination Services System File. State unemployment rate data are taken from the Current Population Survey. | ||||
| NOTES: A total of 12 regressions were estimated: three models for each of the four program groups. For each program group, independent variables were included in a sequential manner. The first model included only state fixed effects. The second model added year fixed effects. The third model added the time-varying variables. The results in this table reflect state-level OLS regression models. Totals may not sum to 100 because of rounding. | ||||
| a. The first row contains the R2 from the first model for each program group. The subsequent two rows reflect the marginal increase in the R2 arising from adding the given group of independent variables to the model. The total of the first three rows represents the R2 for the third model that included all three groups of variables. | ||||
| b. The unexplained variation was calculated by subtracting the R2 for the third model that included all of the predictors from 100 percent. | ||||
I find that adding the three sets of time-varying independent variables to state and time fixed effects in a sequential fashion increases the R2 by 6–18 percent depending on program group. The relative contribution of the three principle sources of time-varying factors is somewhat sensitive to the sequence of adding the three groups of independent variables to the equation.
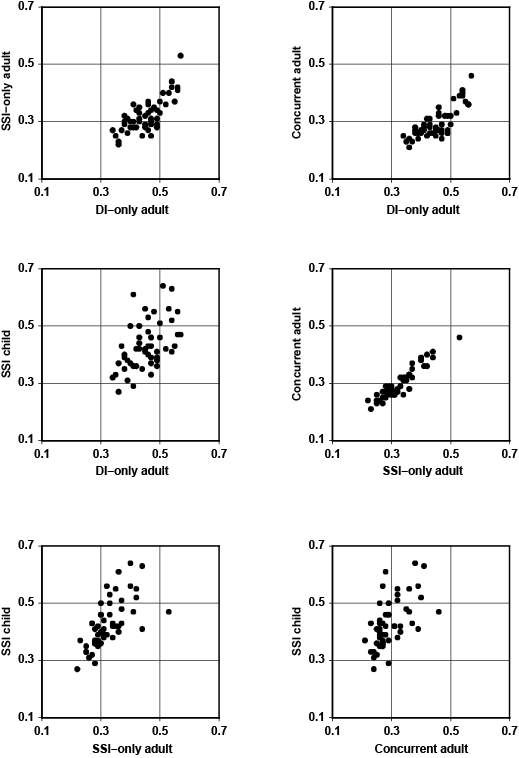
Given the substantial contribution of state fixed effects to the overall variation in allowance rates, Chart 4 shows the average allowance rate by state over the 1993–2008 observation period. The chart demonstrates that long-term observed average differences among the states—in effect the estimated state fixed effects—are substantial. Further analysis of the 1993–2008 average state allowance rates suggests that the long-term average of allowance rates by state is correlated among the program groups. The unweighted r2 between the DI and SSI adult series is 0.66. All of the program groups show a positive correlation with each other as well. The strongest correlation is between the SSI adult and concurrent adult averages by state (r2 = 0.94). The unweighted r2 between the DI-only adult and SSI child series is 0.67. The positive correlation coefficients suggest that relatively permanent differences among the states affect the four program groups similarly. Chart 5 displays scattergrams of the six possible two-way relationships between the state averages for the four program groups during the 1993–2008 period. Of particular interest is the apparent relationship involving the SSI child program group and the three adult program groups. While the visual impression from the chart suggests a relatively strong association between the SSI-only adult and SSI child series as expected, there is clearly some positive relationship even between the DI-only adult and SSI child series as well—a finding that reinforces the inference based on the estimated r2 between the two series discussed earlier. The correlations themselves, of course, do not tell whether the association is due to historical differences in external factors outside of the control of DDS management or to state-to-state differences that are internal to DDSs, but nevertheless the consistent positive association in all six two-way comparisons is remarkable. Disentangling these influences is a worthwhile subject for future research.
Estimated average allowance rate, by state and SSA program group, 1993–2008

| State | Adult group | SSI child | ||
|---|---|---|---|---|
| DI-only | SSI-only | Concurrent | ||
| AK | 0.51 | 0.40 | 0.38 | 0.64 |
| AL | 0.39 | 0.26 | 0.24 | 0.31 |
| AR | 0.44 | 0.25 | 0.26 | 0.35 |
| AZ | 0.46 | 0.37 | 0.35 | 0.48 |
| CA | 0.46 | 0.33 | 0.32 | 0.53 |
| CO | 0.40 | 0.30 | 0.26 | 0.50 |
| CT | 0.47 | 0.31 | 0.27 | 0.39 |
| DC | 0.54 | 0.42 | 0.40 | 0.52 |
| DE | 0.54 | 0.44 | 0.39 | 0.41 |
| FL | 0.38 | 0.32 | 0.28 | 0.39 |
| GA | 0.34 | 0.27 | 0.25 | 0.32 |
| HI | 0.54 | 0.44 | 0.41 | 0.63 |
| IA | 0.49 | 0.29 | 0.26 | 0.39 |
| ID | 0.43 | 0.33 | 0.29 | 0.50 |
| IL | 0.47 | 0.29 | 0.29 | 0.37 |
| IN | 0.40 | 0.28 | 0.27 | 0.37 |
| KS | 0.45 | 0.28 | 0.25 | 0.41 |
| KY | 0.37 | 0.27 | 0.23 | 0.43 |
| LA | 0.41 | 0.28 | 0.29 | 0.29 |
| MA | 0.56 | 0.41 | 0.36 | 0.47 |
| MD | 0.46 | 0.27 | 0.27 | 0.43 |
| ME | 0.50 | 0.33 | 0.29 | 0.46 |
| MI | 0.41 | 0.30 | 0.27 | 0.36 |
| MN | 0.50 | 0.37 | 0.32 | 0.51 |
| MO | 0.47 | 0.25 | 0.24 | 0.33 |
| MS | 0.36 | 0.22 | 0.24 | 0.27 |
| MT | 0.43 | 0.31 | 0.26 | 0.44 |
| NC | 0.39 | 0.31 | 0.26 | 0.38 |
| ND | 0.47 | 0.34 | 0.26 | 0.43 |
| NE | 0.49 | 0.31 | 0.26 | 0.41 |
| NH | 0.57 | 0.53 | 0.46 | 0.47 |
| NJ | 0.55 | 0.37 | 0.37 | 0.43 |
| NM | 0.43 | 0.30 | 0.28 | 0.46 |
| NV | 0.53 | 0.40 | 0.39 | 0.56 |
| NY | 0.49 | 0.34 | 0.32 | 0.38 |
| OH | 0.42 | 0.28 | 0.25 | 0.36 |
| OK | 0.38 | 0.30 | 0.26 | 0.40 |
| OR | 0.45 | 0.32 | 0.27 | 0.56 |
| PA | 0.47 | 0.30 | 0.29 | 0.46 |
| RI | 0.52 | 0.36 | 0.33 | 0.42 |
| SC | 0.38 | 0.29 | 0.27 | 0.35 |
| SD | 0.45 | 0.29 | 0.28 | 0.42 |
| TN | 0.35 | 0.25 | 0.23 | 0.33 |
| TX | 0.42 | 0.34 | 0.31 | 0.42 |
| UT | 0.41 | 0.36 | 0.28 | 0.61 |
| VA | 0.46 | 0.36 | 0.33 | 0.40 |
| VT | 0.56 | 0.42 | 0.36 | 0.55 |
| WA | 0.48 | 0.35 | 0.32 | 0.55 |
| WI | 0.49 | 0.28 | 0.27 | 0.36 |
| WV | 0.36 | 0.23 | 0.21 | 0.37 |
| WY | 0.43 | 0.35 | 0.31 | 0.42 |
Bivariate relationship between average state allowance rates for various combinations of SSA program groups, 1993–2008
Conclusions
Overall, I find that the probability of an initial allowance is clearly affected by demographic characteristics, diagnostic mix, and the local unemployment rate in the expected direction. All of these factors are outside the control of DDS decision makers; therefore, accounting for their role should help in comparing allowance rates across DDS units on a footing more equal than the comparison of raw initial allowance rates.
The empirical results show that—
- Older adult disability applicants are more likely than younger adult applicants to experience a favorable outcome of the initial disability determination, regardless of SSA program group (DI, SSI, or both). The reverse is true for childhood SSI applicants. Adult applicants with a musculoskeletal primary diagnosis are less likely to experience a favorable initial disability determination outcome than applicants with other diagnoses, regardless of program group. In contrast, adult applicants with intellectual disabilities, neoplasms, and genitourinary diagnoses are relatively more likely to receive a favorable initial determination result. The relationship between primary diagnosis and the likelihood of an initial allowance is generally similar for adult and childhood applicants.
- An increase in the state unemployment rate tends to be associated with a decrease in the initial allowance rate. This relationship holds for all three adult program groups and childhood SSI applications. The negative relationship between unemployment and initial allowances is particularly strong for "mental" diagnoses for all three adult program groups and for SSI children. The negative relationship is statistically significant, and it is comparable in magnitude for musculoskeletal diagnoses for all three adult program groups. Interestingly, only the DI-only adult coefficient is statistically significantly different from zero for neoplasms, and even that point estimate is relatively low in absolute value. Note that (a) neoplasms are invariably "doctor diagnosed" health conditions and (b) award decisions may be more likely to be made at the "meet the listings" step in the disability determination process, compared with determinations regarding mental and musculoskeletal impairments. Both of these indicate the relatively major role of objective factors for neoplasms, and therefore it is not surprising that we estimate award probabilities for the neoplasms diagnostic group that are relatively less likely to be responsive to business cycle conditions.
- Estimates based on individual-level data are generally comparable to estimates from similarly specified models based on state-level models. An important advantage of access to data on individual characteristics of applicants is that it provides maximum flexibility for program group analyses and model specification.
- Using the fixed-effects models substantially contribute to predictability of the variation of state allowance rates. A substantial portion of state-to-state variation in allowance rates is explained by relatively permanent differences among the states and year-to-year changes affecting all states. The state fixed effects reflect differences among the states that are long term, that is, they affect average state differences for the whole 1993–2008 study period. The year fixed effects reflect factors, such as legislative changes, that affect all states during a given year. The models allow for the measurement of variation attributable to these two sources, but do not provide specific reasons for their explanatory power. Time-varying factors accounted for by the models include demographic and diagnostic characteristics of applicants and the state unemployment rate, which provide additional contribution to explained variation. The three groups of variables included in the regression models (state fixed effects, time fixed effects, and time-varying factors) together explain 73–84 percent of total variation. Sixteen to 27 percent of the total variation in state allowance rates (depending on SSA program group) is not explained by fixed effects and time-varying factors explicitly considered in the models.
Various future research directions might be productive. An obvious extension to this study would be to replicate it using data that are more recent. Accounting for the role of state and year fixed effects and time-varying exogenous factors should be helpful in refining projections of initial allowance rates. A logical direction of follow up could extend this analysis to research on factors affecting ultimate allowance rates and lifetime benefit streams. Of particular interest with respect to lifetime benefit streams is the question of whether the exit rates of marginally qualifying applicants who were awarded benefits during periods of high unemployment are higher than the exit rates of others who were first awarded benefits during more favorable labor market conditions. Another potentially fruitful area of future research might focus on the temporal dynamics (lag structure) of the relationship between unemployment shocks and disability allowance rates. Yet another potentially promising area might involve studies designed to analyze various mechanisms that may be responsible for the relationship between the unemployment rate and initial determination results. Some may be external to the disability determination system; others may involve programmatic responses to external shocks, such as sudden increases in applications arising from worsening labor market conditions or other factors.
While this study does not focus on possible responses by DDS administrators or caseworkers, and the recent work of Maestas, Mullen, and Strand (2011) did not analyze the effects of local labor market conditions on DDS decision making, a file adding longitudinal data on caseworker characteristics to this analysis file might facilitate future work on the relationship between the business cycle and DDS decision making.
Notes
1 Some applicants initially denied are subsequently allowed. Ultimate allowance rates are of obvious interest to the Social Security Administration, but beyond the scope of the current analysis. In this article, I focus on the initial allowance rates—an analysis that is a necessary first step in any study of ultimate allowance rates.
2 An important broader context is health insurance coverage. Adverse labor market conditions may reduce access to private health insurance. In contrast, SSI awardees are automatically eligible for Medicaid in most cases, while DI awardees are eligible for Medicare after a combined 5-month DI waiting period and a 24-month Medicare waiting period.
3 Initial determinations are made by state DDS units. "Technical denials" made by SSA field offices prior to the initial disability determination process are not included in the analysis sample. Technical denials are the result of evidence that the applicant does not meet the nondisability criteria for either DI or SSI benefit eligibility. Applicants who are neither DI-insured nor meet the SSI means test are typically denied by SSA field office staff, and no records are forwarded to the DDS.
4 There are five steps in the initial determination process. Those involve the assessment of whether the applicant (1) is working at the SGA level, (2) has a "severe" condition, (3) has a severe condition that is included in the list of disabling conditions, (4) can do the work he or she did previously, and (5) can do any other type of work. Initial allowances can be made at steps 3 and 5. Initial denials can be made at steps 1, 2, 4, and 5 (http://www.socialsecurity.gov/dibplan/dqualify5.htm). This article focuses on initial determinations and does not address possible reversals of denials at subsequent levels (reconsideration and appeals).
5 The author uses variation in coal prices in the Appalachian region arising from the Organization of the Petroleum Exporting Countries (OPEC) oil embargo and a subsequent bust in the coal market in the 1980s to identify the impact of labor market conditions on DI and SSI program participation.
6 The current review focuses on literature subsequent to the publication of Rupp and Stapleton (1995). That study included an extensive review of previous studies, but did not identify any that specifically focused on initial allowance rates. The pioneering work of Mordechai Lando, and others at SSA in the 1970s, focused on the relationship between applications and the unemployment rate, but included a few separate estimates on the relationship between awards and the unemployment rate (Lando 1979).
7 The list of primary diagnoses is as follows: infectious and parasitic diseases; neoplasms; endocrine, nutritional, and metabolic diseases; mental disorders (not including intellectual disabilities); intellectual disabilities; diseases of the blood and blood forming organs, nervous system, circulatory system, respiratory system, digestive system, genitourinary system, skin and subcutaneous tissue, musculoskeletal system and connective tissue; congenital anomalies; and other disorders.
8 Variables, such as the presence of a secondary diagnosis, are often included in models of this kind to capture some unmeasured factors. The inclusion of such control variables helps to reduce estimation bias with respect to the variables of key interest, but their coefficients may not have a straightforward causal interpretation.
9 I use the Wooldridge test for autocorrelation in panel data using the xtserial procedure in STATA and correct for autocorrelation using the xtgls procedure.
10 The file is based on information from Form SSA-831. (See SSA Program Operations Manual, Section DI 26510.001, extracted from https://secure.ssa.gov/poms.nsf/lnx/0426510001 on April 30, 2012.)
11 The prevalence of disability and applications tended to rise sharply for people in their fifties and early sixties. The estimates in this study show a sharp increase in the marginal effect between the 50–54 age group and the 55–59 group. Those differences may reflect unmeasured changes in the characteristics of applicants or the effect of the rules and implementation practices related to vocational factors.
12 Note that 26 of the 35 nonsignificant coefficients are negative, suggesting that small subsample size rather than the lack of true negative effects may be the more important reason for lack of statistical significance for the individual coefficients.
13 Note that although the scope of this study is limited to factors affecting initial allowances, I also test a state-level, fixed-effects model with the natural logarithm of the number of initial determinations as the dependent variable. The estimates (not shown) indicate substantial positive effects of changes in the unemployment rate on initial determinations for all four SSA program groups, a finding consistent with past studies estimating a positive relationship between the unemployment rate and applications or initial determinations.
14 Note that the individual-level and aggregate models use the exact same data set and model specification except for the functional form (logit versus OLS), thus the comparisons are not affected by extraneous factors arising from possible differences in the source data themselves.
15 A self-weighting sample arises from selection with a constant probability.
16 This interpretation is supported by information on the standard error of state allowance rates from the micromodels. For example, the standard error of the DI-only sample's average allowance probability is 0.0021 for California, 0.0024 for New York, and 0.0026 for Texas. In contrast, the corresponding numbers are 0.0162, 0.0154, and 0.0153 for Wyoming, Alaska, and the District of Columbia (DC), respectively. Thus, the standard error of state allowance rates in those two small states and DC is over 1.5 percentage points compared with the much smaller standard error (below 0.3 percentage points) for the three large states cited first.
17 The relative contribution of year effects and state effects is fairly invariant to the sequential order of introducing the two sets of predictors to the regression equation, reflecting an additive relationship.
References
Autor, David H., and Mark G. Duggan. 2003. "The Rise in the Disability Rolls and the Decline in Unemployment." Quarterly Journal of Economics 118(1): 157–205.
Black, Dan, Kermit Daniel, and Seth Sanders. 2002. "The Impact of Economic Conditions on Participation in Disability Programs: Evidence From the Coal Boom and Bust." American Economic Review 92(1): 27–50.
Burkhauser, Richard V., J. S. Butler, and Robert R. Weathers II. 2001/2002. "How Policy Variables Influence the Timing of Applications for Social Security Disability Insurance." Social Security Bulletin 64(1): 52–83.
Coe, Norma B., Kelly Haverstick, Alicia H. Munnell, and Anthony Webb. 2011. "What Explains State Variation in SSDI Application Rates?" CRR Working Paper 2011-23. Chestnut Hill, MA: Center for Retirement Research at Boston College. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1970314.
Duggan, Mark, and Scott A. Imberman. 2008. "Why Are the Disability Rolls Skyrocketing? The Contribution of Population Characteristics, Economic Conditions, and Program Generosity." In Health at Older Ages: The Causes and Consequences of Declining Disability Among the Elderly, edited by David Cutler and David Wise, 337–379. Chicago, IL: University of Chicago Press.
Guo, Xuguang, and John F. Burton Jr. 2008. "The Relationship Between Worker's Compensation and Disability Insurance." In LERA Series: Proceedings of the 60th Annual Meeting, edited by Adrienne E. Eaton, 29–37. Champaign-Urbana, IL: Labor and Employment Relations Association.
———. 2012. "The Growth of Applicants for Social Security Disability Insurance: A Spillover Effect From Workers' Compensation." Social Security Bulletin 72(3): 69–88.
Kreider, Brent. 1999. "Social Security Disability Insurance: Applications, Awards, and Lifetime Income Flows." Journal of Labor Economics 17(4): 784–827.
Lando, Mordechai E., 1979. "Prevalence of Work Disability by State, 1976." Social Security Bulletin 42(5): 41–44.
Maestas, Nicole, Kathleen J. Mullen, and Alexander Strand. 2011. "Does Disability Insurance Receipt Discourage Work? Using Examiner Assignment to Estimate Causal Effects of SSDI Receipt." RAND Labor and Population Working Paper Series No. WR-853.3 (March 10). http://www.rand.org/content/dam/rand/pubs/working_papers/2012/RAND_WR853-3.pdf.
Rupp, Kalman, and David Stapleton. 1995. "Determinants of the Growth in the Social Security Administration's Disability Programs—An Overview." Social Security Bulletin 58(4): 43–70.
Soss, Joe, and Lael R. Keiser. 2006. "The Political Roots of Disability Claims: How State Environments and Policies Shape Citizen Demands." Political Research Quarterly 59(1): 133–148.
Stapleton, David, Kevin Coleman, Kimberly Dietrich, and Gina Livermore. 1998. "Empirical Analyses of DI and SSI Application and Award Growth." In Growth in Disability Benefits, edited by Kalman Rupp and David C. Stapleton, 31–92. Kalamazoo, Michigan: W. E. Upjohn Institute for Employment Research.
Stapleton, David, Kimberly Dietrich, and Gilbert Lo. 1995. Public Use Data File on the Social Security Administration's Disability Programs. Documentation for the Public Use Data File, prepared under HHS contract no. 100-0012 for the Department of Health and Human Services, Office of the Assistant Secretary for Planning and Evaluation (October 24). Fairfax, VA: Lewin-VHI.
Strand, Alexander. 2002. "Social Security Disability Programs: Assessing the Variation in Allowance Rates." ORES Working Paper Series No. 98. Washington, DC: Social Security Administration (August).