Heterogeneity in Health and Mortality Risk Among Early Retiree Men
ORES Working Paper No. 105 (released May 2004)
Hilary Waldron is with the Division of Economic Research; Office of Research, Evaluation, and Statistics; Office of Policy; Social Security Administration.
Acknowledgments: The author would like to thank Edward DeMarco, Harriet Duleep, Susan Grad, Howard Iams, Preston Jacobs, Mike Leonesio, Joyce Manchester, Karen Morris, David Pattison, and David Weaver for their helpful comments and suggestions. The author would also like to thank Bert Kestenbaum for having the foresight to update the 1973 Exact Match, without which this analysis would not have been possible.
Working papers in this series are preliminary materials circulated for review and comment. The findings and conclusions expressed in them are the authors' and do not necessarily represent the views of the Social Security Administration.
Summary
Conventional wisdom holds that the majority of early retirees are in good health and that only a minority are in poor health. This wisdom is based on examinations of levels of health among the early retiree population. In contrast, this paper looks at both the health and mortality risk of early retirees relative to the health and mortality risk of full retirement-age retirees. For all men studied in this paper, the full retirement age was 65, so they are subsequently referred to as age 65 retirees. Health is examined with data from the Survey of Income and Program Participation matched to Social Security earnings and benefit data. Mortality is examined with data from the 1973 Current Population Survey matched to Social Security earnings, benefit, and death data. The analysis is restricted to men who live to at least age 66 and who have never received Social Security Disability Insurance benefits.
This paper finds substantial heterogeneity among early retirees in health and mortality risk related to the age at which they become entitled to Social Security benefits. Early retirees consist of (1) a group in extremely poor health, (2) a group with health equal to age 65 retirees, and (3) a group with health in between that of the first two groups. The majority of early retirees are in poorer health and have higher mortality risk than that of age 65 retirees, and only a minority have health and mortality risk as good as that of age 65 retirees. Other findings include the following:
- In general, the earlier men retire, the more likely they are to be in poorer health and have higher mortality risk than those retiring at age 65. Some, but not all, of this difference is explained by early retirees being more likely to have low education and average lifetime earnings.
- When the age at which men retire is further subdivided by average lifetime earnings, even most early retirees with earnings in the top quarter of the earnings distribution have poorer health and higher mortality risk than do most men retiring at age 65. In addition, men in the top quarter of the earnings distribution retiring as soon as possible (exactly age 62 to age 62 and 2 months) have greater mortality risk than do most men retiring at ages 62 and 3 months to ages 62 and 11 months, age 63, and age 64, regardless of the average lifetime earnings of men claiming benefits at these later ages of early retirement.
- The small group of early retirees equal in health and mortality risk to age 65 retirees is most likely to be in the top quarter of the earnings distribution and to retire at age 64.
- When age of retirement is further subdivided by receipt of a pension other than Social Security, early retirees with pensions are both in poorer health than all age 65 retirees and in better health than early retirees without pensions.
- However, the level of income in early retirees' pensions does matter. Early retirees with pension income in either the bottom 50th or bottom 75th of the income distribution (depending on the reference variable used) are more likely to be in poorer health than are age 65 retirees, while early retirees with pension income in the top half or top quarter of the distribution are equal in health to age 65 retirees.
- There may be some heterogeneity among age 65 retirees, but it is hard to reach conclusiveness on this point. Age 65 retirees with earnings in the bottom quarter of the distribution appear to be in better health than early retirees in the same earnings quarter, but in poorer health than most higher-earning early and age 65 retirees. On the other hand, life expectancy differences between age 65 retirees with earnings in the bottom quarter of the earnings distribution and other age 65 retirees are not found.
- Life expectancy differences by education have widened over time, even after controlling for the changing proportions of men in each education category by birth cohort.
Introduction
This paper focuses on three views of early retirees—(1) a health dichotomy school of thought, (2) a benefits optimization school of thought, and (3) a health trichotomy school of thought, which is a combination of the previous two views. The health dichotomy school of thought proposes that early retirees include two broad groups of people, those with severe health problems who are unable to work and unable to qualify for Social Security disability benefits and those with health as good as that of age 65 retirees who choose to retire for reasons other than health. Because the benefits optimization school of thought is perhaps less well known than the others, it is discussed in more detail. In the following discussion, note that the focus of the benefits optimization idea is on differences in longevity, not health. The assumption is that any observed differences in health revealed in this paper will carry over into observed differences in mortality risk.
According to the benefits optimization idea, if benefits are actuarially reduced to reflect average mortality, then workers with higher than average mortality will retire early and workers with lower than average mortality will retire late, other things being equal. (This paper ignores the added complications of a claiming decision based on a couple's best interest rather than an individual's best interest.) Note that the key here is the position of workers relative to average mortality rather than their absolute levels of health. This type of idea is developed as a theoretical model in Simonovits (2001). In his model, the government observes the average life expectancy of a pool of workers, and the individual observes his or her own life expectancy, creating an asymmetric information situation in which an individual optimizes length of employment (age of retirement) based on his or her own lifespan in relation to the government average. This idea is also discussed in Sammartino (1987, 37) in which he writes:
If the returns in expected future benefits from delaying retirement past age 62 are roughly fair for the average older worker, then they necessarily are less than fair for a worker in poor health facing less than average life expectancy. This will cause a convex kink in the budget constraint at that age, and hence a clustering of retirement at that point.
Empirically, Duggan and Soares (2001) independently complement Simonovits' work when they examine the relationship between statutory actuarial equivalence (which is built into Social Security law) and actuarial equivalence (based on survival probabilities that differ by sex and earnings quintiles). Actuarial equivalence is defined as a benefit adjustment before full retirement that "equates the present value of benefits that begin at [that] age with the present value of benefits that begin at the normal retirement age" (Duggan and Soares 2001, 4).1 They find that most men gain financially by claiming benefits before age 65 and that most women gain financially by postponing claiming until at least age 64. Only men in the top quintile of lifetime earnings gain by delaying benefit receipt for nearly 2 years.
The benefits optimization idea does not imply that Social Security's actuarial adjustments are incorrect on average. A RAND report (2002, 117–118) finds that "the early retirement penalty is roughly actuarially fair." Because an individual's life expectancy varies around the average, if one had perfect information and knew each person's exact date of death, one could actuarially adjust each individual's benefits so that the present value of his or her benefits at age 62 exactly equaled their value at age 65; of course in practice this is impossible. Thus, actuarial adjustments that are fair on the macro level can be unfair on the micro level and cause clustering of individuals with lower than average life expectancy at the youngest available age.
To understand the differences and similarities between the health dichotomy school of thought, the benefits optimization school of thought, and a health trichotomy school of thought, retirees are placed into four groups:
- Group A = early retirees in extremely poor health (low life expectancy).
- Group C = early retirees with health (life expectancy) equal to that of age 65 retirees.
- Group B = early retirees with health (life expectancy) in between that of Group A and Group C.
- Group D = age 65 retirees.2
Under the health dichotomy school of thought (A < C = D; B is not included), early retirees in extremely poor health should self-report poorer health and have an average life expectancy shorter than that of age 65 retirees, while all other early retirees should self-report health and have an average life expectancy no different from that of age 65 retirees. Under the benefit optimization school of thought (A < B < D; C is not included), this latter group of all other early retirees should self-report poorer health and have a life expectancy shorter than that of age 65 retirees. Under the trichotomous school of thought (A < B < C = D), the group of early retirees not in extremely poor health will consist of both retirees with poorer health and shorter life expectancies than age 65 retirees and retirees with health and life expectancies equal to age 65 retirees.
The three competing views of early retirees are not mutually exclusive. In all three views, there is a group of early retirees in poorer health than age 65 retirees (A < D). However, the benefits optimization and trichotomy ideas allow for more heterogeneity among early retirees. Those ideas suggest that early retirement should exhibit a correlation with poorer health or mortality risk, rather than be completely random, once the poor health minority is controlled for (A < B < D).
Empirical estimates of the existence and size of groups A, B, C, and D have important implications for policy recommendations regarding changes in Social Security's early retirement age. Under any one of the three schools of thought, raising the early retirement age would not have a distributionally neutral effect across workers; rather, it would affect individuals with lower life expectancy (poorer health) to a greater extent than individuals with average or higher than average life expectancy (health). While recognizing this fact, some analysts still recommend raising the early retirement age under the assumption that the group that would be adversely affected is small enough to target through other programs. (Policy suggestions have included making changes in the Social Security Disability Insurance (DI) program to allow this group on the rolls or lowering the eligibility age for Supplemental Security Income (SSI)-aged benefits from 65 to 62 (Social Security Advisory Board 1999). If either the benefits optimization or the health trichotomy school of thought turns out to be a more accurate description of early retirees, then the number of workers affected by a change in the early retirement age would be much greater than the number that conventional wisdom based on the health dichotomy school of thought tends to assert. In addition, a frequent argument used by proponents of raising the early retirement age is that if more people work beyond age 62, the productive capacity of the economy will increase (Social Security Advisory Board 1999). Once again, the empirical distribution of early retiree characteristics matters in this argument. Because the health dichotomy school of thought believes that the majority of early retirees are equal in health to age 65 retirees, proponents also believe that the majority of early retirees would be as productive as age 65 retirees if they had worked from ages 62 to 64, like their age 65 retiree counterparts. If the data show that the majority of early retirees are in poorer health than age 65 retirees, then projections of their productivity may need to be adjusted downward to allow for the dampening effect of poor health on worker productivity.
To explore the three competing views of early retirees, this paper presents empirical results on relative health differences between early and age 65 retirees and then gives empirical results on relative mortality risk differences between early and age 65 retirees. In the 1992/1993 Survey of Income and Program Participation (SIPP) matched to the Social Security Administration's (SSA's) administrative data, self-reported health is the dependent variable. The paper first measures the correlations between age of retirement, education, earnings, race, and self-reported health, and then it measures heterogeneity in the variables for early age of retirement as measured by average lifetime earnings, receipt of a pension other than Social Security, and level of non–Social Security pension income. In the 1973 Current Population Survey (CPS) matched to Social Security administrative data (the 1973 Exact Match), death is the dependent variable. The paper measures the correlations between age of retirement, education, earnings, race, and mortality risk, and then it measures heterogeneity in the variables for early age of retirement as measured by average lifetime earnings.
Empirical Results on Health Using Matched SIPP/SSA Data
Studies such as Burkhauser and others (1996), Uccello (1998), Smith (1999), and RAND (2002) have found that the majority of men retiring at age 62 are in good health, with only a minority reporting poor health. In contrast, the statistical technique used in this paper measures relative health, rather than levels of health. Thus, while the aforementioned studies are designed to describe incidence of poor health in the Social Security retired-worker male population, this study is designed to compare the health of early retirees to that of age 65 retirees in relative terms.3,4 The question posed here is whether early retirees are in poorer health than age 65 retirees, not whether early retirees are in poor health. A relative method of analysis allows evidence for a benefits optimization or health trichotomy state of the world to be captured empirically—if such evidence exists—by capturing distinctions between the likelihood of different groups of retirees' states of health.
If the composition of early retirees is more complex than a poor health minority and a majority indistinguishable from age 65 retirees, heterogeneity among early retirees is important. For example, assume that retirees in the worst health claim benefits at exactly age 62. If all other early retirees are indistinguishable from age 65 retirees, then it is an acceptable analytical technique to compare age 62 retirees with all other retirees. On the other hand, if retirees at age 63 and age 64 are also self-selecting into pre-age 65 retirement for health or mortality reasons, then such an analytical technique creates a skewed view of early retirees. In the same way, if individuals claiming benefits at exactly age 62 represent a self-selection of the most unhealthy or short-lived retirees, then combining those retirees with age 63 and age 64 retirees will create a skewed view of early retirees. In the former instance, the magnitude of the contrast between age 62 retirees and all other retirees will be attenuated by age 63 and age 64 retirees who are grouped in the reference variable with age 65 retirees. In the latter instance, the magnitude of the contrast between exactly age 62 retirees and age 65 retirees will be attenuated by age 63 and age 64 retirees—who are not in as poor health or as short-lived as exactly age 62 retirees.
For the discussions in this paper, it is assumed that poor health is strongly correlated with shorter life expectancy. Evidence of this correlation is found in Idler and Benyamini's (1997) summary of 27 separate studies in which self-reported health is tested as a predictor of mortality. This section of the paper uses differences in self-reported health to describe early retirees, while the following mortality section uses differences in mortality risk.
Data Description
This study uses a version of the 1992/1993 Survey of Income and Program Participation, referred to as the 1992/1993 look-alike SIPP, developed by the Urban Institute under contract to SSA for the purpose of producing SIPP files that are formatted to look like March 1994 CPS data.5 The 1992/1993 look-alike SIPP is matched to Social Security administrative data that include beneficiary, claim, and death data from the date of the respondent's entitlement through the end of 1996 (Master Beneficiary Record, or MBR) and earnings data (Summary Earnings Record, or SER) from 1951 through 1999. The subsample used for this analysis consists of male retired-worker beneficiaries, excluding men who have ever received Social Security DI benefits, who survived until at least age 66.6 By employing the survival restriction, all men observed have an equal chance of claiming benefits from exactly AGE62A through AGE65. Note that this technique does have the effect of eliminating men who retired early but who did not survive to age 66. Thus, it is conservative in that the most severe early retirement cases are dropped from the sample. (In practice, this only amounts to 10 out of 4,135 men, so it has no practical effect on the estimates.) Male retired-worker beneficiaries is a term that refers to the subset of beneficiaries who are being paid benefits based on their own earnings record. To qualify, individuals must be Social Security-insured and aged 62 or older. Woman are not analyzed because of concerns that women in the birth cohorts covered do not have extensive work histories, both reducing their chance of receiving retired-worker benefits on their own record and limiting the effectiveness of using earnings to proxy for observed heterogeneity. All data in this section (excluding Table 2) are unweighted.
In Table 1, the last full year of MBR (death) data is 1996, and 1930 is the youngest cohort used so that deaths before age 66 are observable for all cohorts. Because earnings data are first available for 1951, 1906 is the oldest birth cohort allowed so that earnings from ages 45 through 55 are observable for all cohorts. (The oldest cohort is age 45 in 1951, and the youngest cohort is age 55 in 1985.) This allows the same earnings measure to be used for all birth cohorts.
| Category | Unweighted count |
|---|---|
| Male retired-worker beneficiaries— | 4,975 |
| Born from 1906 through 1930 | 4,135 |
| Surviving to at least age 66 | 4,125 |
| Minus those entitled at age 66 or older | 3,987 |
| Minus those with missing self-reported health | 3,974 |
| With some nonzero earnings from ages 45 through 55 | 3,818 |
| Years of birth | |
| 1906–1909 | 201 |
| 1910–1913 | 337 |
| 1914–1917 | 527 |
| 1918–1921 | 713 |
| 1922–1926 | 1,118 |
| 1927–1930 | 922 |
| SOURCE: Author's tabulations using the 1992/1993 look-alike Survey of Income and Program Participation. | |
Explanatory Variables
In this section, variables that are used and expounded upon in the health analysis portion of the paper are defined.
Self-Reported Health. Respondents rate their health as poor, fair, good, very good, or excellent. This variable is observed in the 1992/1993 SIPP.
Age at the Time of Health Question. This variable measures the age at which respondents answer the self-reported health question described earlier. Age at response ranges from 62 years and 10 months to 87 years and 10 months. This variable is used as a control for the natural deterioration of health with age. Because age and cohort effects are not measured separately, the variable also captures any health effects specific to a particular birth cohort. Year of birth is observed in SSA's administrative data, and the timing of the question is observed in the 1992/1993 SIPP.
Retirement Age. The retirement age (defined as the Social Security age of entitlement) of each beneficiary, measured in months, is grouped into five categories for estimation. The first category, AGE62A, includes individuals who claim benefits as soon as they possibly can. Thus, individuals who are entitled at exactly age 62 to age 62 and less than 3 months are in this category. The category is not just restricted to exactly age 62 because of benefit claiming complications brought on by the timing of individuals' birthdays (Olson 1999). Empirically, the biggest spike in claiming is at age 62 and 1 month, so it was decided to extend the variable an additional month past the spike to allow for possible inconsistencies in the administrative data. The other retirement-age categories used are age 62 and 3 months to age 62 and 11 months (AGE62B), age 63 to age 63 and 11 months (AGE63), age 64 to age 64 and 11 months (AGE64), and age 65 to age 65 and 11 months (AGE65). Beneficiaries are first eligible to retire at either age 62 or age 62 and 1 month (depending on the date of their birthday) under Social Security rules. For the birth cohorts observed here, age 65 is the full retirement age or age of entitlement for which unreduced benefits are first available. This variable is observed in SSA's administrative data.
Race. Because of sample size considerations, estimates are only made for the effect of being black on self-reported health. This variable is observed in the 1992/1993 SIPP.
Education. Educational attainment is grouped into three categories for estimation: less than 12th grade (edu1), 12th grade through an associate's degree (edu2), and a bachelor's degree or higher (edu3). These categories are used because they are the closest to those constructed in the mortality section using the 1973 Exact Match (CPS). This variable is observed in the 1992/1993 SIPP.
Earnings. Nonzero average relative earnings from ages 45 through 55 are used to estimate the effect of earnings level on self-reported health. Average relative earnings are grouped into four categories for estimation that correspond to the following four positions in the earnings distribution: 0–25th percentile (earn1), 26th–50th percentile (earn2), 51st–75th percentile (earn3), and 76th–100th percentile (earn4). Earnings from ages 45 through 55 for each individual are measured relative to the national average wage that corresponds to the year in which the earnings are recorded in the administrative earnings records. The relative earnings are then averaged over the number of years each individual has nonzero earnings from ages 45 through 55. To avoid unintended interactions between year of birth and earnings level, the position of an individual's average relative nonzero earnings amount in the earnings distribution (used to construct the four dummy earnings variables) is based on the distribution of average nonzero relative earnings for that individual's year of birth. Zeros are not averaged in because the administrative earnings records do not allow one to distinguish between periods of unemployment and periods of employment in non–Social Security–covered earnings.7 Before earnings from ages 45 through 55 can be averaged, earnings limited by the Social Security taxable maximum are imputed using a tobit regression. (For details on the imputation method, see the appendix.)8 Earnings are observed in SSA's administrative data.
Pension Receipt. This variable measures whether respondents received any pension or retirement income other than Social Security. To compute pension statistics, the sample is restricted to men who were entitled to Social Security retired-worker benefits by their age at interview to eliminate most men who did not receive a pension at the time of the interview, but who will subsequently receive one. This decreases the sample size to 3,488. (Regressions performed without the pension variable are performed on the larger sample of 3,818.) Even so, it is possible that some men will begin receiving a pension sometime after becoming entitled to Social Security benefits. Some of these men could be classified as not receiving a pension in this analysis, because the pension variable is a point-in-time observation. Pension receipt is observed in the 1992/1993 SIPP.
Preliminary Statistics
Before proceeding with the multivariate analysis, the distribution of the sample by some of the explanatory variables is examined (Table 2). AGE65 retirees have the smallest proportions of men in the lowest education and earnings categories and the largest proportions of men in the highest education and earnings categories. A greater proportion of AGE65 retirees (75 percent) are in either good, very good, or excellent health than are AGE62A retirees (66 percent). A smaller proportion of AGE65 retirees—who otherwise appear on average to be of higher socioeconomic status—received a pension other than Social Security than did AGE62A retirees.
| Variable | N | Full sample |
AGE62A (n = 1,462) |
AGE62B (n = 396) |
AGE63 (n = 375) |
AGE64 (n = 825) |
AGE65 (n = 760) |
|---|---|---|---|---|---|---|---|
| Education (years) | |||||||
| Less than 12 | 1,342 | 35.3 | 39.0 | 43.5 | 36.3 | 34.5 | 24.1 |
| 12–15 | 1,755 | 45.5 | 48.4 | 40.8 | 46.5 | 45.8 | 41.8 |
| 16 or more | 721 | 19.2 | 12.7 | 15.7 | 17.2 | 19.7 | 34.1 |
| Earnings (percentiles) | |||||||
| 0–25th | 965 | 25.4 | 28.9 | 27.1 | 25.8 | 26.1 | 16.6 |
| 26th–50th | 951 | 24.9 | 24.5 | 24.6 | 25.8 | 26.1 | 24.2 |
| 51st–75th | 958 | 24.9 | 23.6 | 23.5 | 25.0 | 24.4 | 28.8 |
| 76th–100th | 944 | 24.8 | 23.0 | 24.7 | 23.5 | 23.4 | 30.5 |
| Self-reported health | |||||||
| Poor | 388 | 10.3 | 12.6 | 10.1 | 10.7 | 9.2 | 7.1 |
| Fair | 778 | 20.3 | 22.1 | 17.1 | 23.3 | 18.9 | 18.4 |
| Good | 1,402 | 36.7 | 35.4 | 36.4 | 37.4 | 39.6 | 35.9 |
| Very good | 844 | 22.0 | 20.5 | 25.0 | 20.0 | 22.3 | 24.2 |
| Excellent | 406 | 10.7 | 9.5 | 11.4 | 8.7 | 10.0 | 14.4 |
| Received pension other than Social Security a | 2,120 | 60.7 | 64.5 | 65.6 | 58.8 | 54.6 | 57.2 |
| SOURCE: Author's tabulations using the 1992/1993 look-alike Survey of Income and Program Participation (SIPP). | |||||||
| NOTES: Although this table is intended to describe the sample used in this analysis, not the U.S. population, percentages are calculated using SIPP weights in deference to analysts who prefer SIPP tabulations weighted. Unweighted percentages did not differ much from weighted percentages. Sample counts are unweighted to show sample sizes. | |||||||
| a. Sample (3,488) is restricted to men who were entitled to Social Security retired-worker benefits as of their interview. | |||||||
Because the age at the time the health question was asked is not controlled for in Table 2, ordered logistic regressions are conducted in which year of birth (which is synonymous with age at the time of the health question) is controlled for in order to obtain a more rigorous first look at the data. The dependent variable has five levels—AGE62A, AGE62B, AGE63, AGE64, and AGE65. Ordered logits are set up to predict the log-odds of a man retiring at a younger (earlier) age rather than an older (later) age. Year of birth should be positive, because of the trend toward early retirement over the birth cohorts in the sample.
Empirically, when each effect is estimated separately, men in poor health have odds of retiring early 2.3 times those of men in excellent health; men with less than a high school education have odds 3 times those of college graduates; and men with average relative lifetime earnings in the bottom quarter of the distribution have odds 1.5 times those of men with earnings in the top quarter of the distribution (Table 3, Models 1, 2, and 3). Note that even with socioeconomic controls, men in poor, fair, or good health still have greater odds (1.74, 1.39, and 1.20, respectively) of retiring earlier than do men in excellent health (Table 3, Model 4).
| Variable | Model 1. | Model 2. | Model 3. | Model 4. | ||||
|---|---|---|---|---|---|---|---|---|
| Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
|
| Poor health b | 0.8376 (0.1314)* |
2.3 (1.79–3.0) |
n.a. | n.a. | n.a. | n.a. | 0.5556 (0.135)* |
1.74 (1.34–2.27) |
| Fair health b | 0.5801 (0.1120)* |
1.79 (1.43–2.23) |
n.a. | n.a. | n.a. | n.a. | 0.3302 (0.1149)* |
1.39 (1.11–1.74) |
| Good health b | 0.3528 (0.102)* |
1.42 (1.17–1.74) |
n.a. | n.a. | n.a. | n.a. | 0.1853 (0.1039)** |
1.2 (0.98–1.48) |
| Very good health b | 0.1943 (0.1087)** |
1.21 (0.98–1.50) |
n.a. | n.a. | n.a. | n.a. | 0.1333 (0.1097) |
1.14 (0.92–1.42) |
| Earn1 c | n.a. | n.a. | n.a. | n.a. | 0.4301 (0.0834)* |
1.54 (1.31–1.81) |
0.1449 (0.0874)* |
1.16 (0.97–1.37) |
| Earn2 c | n.a. | n.a. | n.a. | n.a. | 0.1586 (0.0829)** |
1.17 (1.00–1.38) |
-0.0497 (0.0852) |
0.95 (0.81–1.12) |
| Earn3 c | n.a. | n.a. | n.a. | n.a. | 0.024 (0.0826) |
1.02 (0.87–1.20) |
-.0559 (.0835) |
0.95 (0.80–1.11) |
| Edu1 d | n.a. | n.a. | 1.107 (0.0858)* |
3.03 (2.56–3.58) |
n.a. | n.a. | 0.9797 (0.0913)* |
2.66 (2.23–3.19) |
| Edu2 d | n.a. | n.a. | 0.8345 (0.0806)* |
2.30 (1.97–2.70) |
n.a. | n.a. | 0.7839 (0.0826)* |
2.19 (1.86–2.58) |
| Year of birth | 0.0558 (0.00485)* |
1.06 (1.05–1.07) |
0.057 (0.00483)* |
1.06 (1.05–1.07) |
0.0487 (0.00472)* |
1.06 (1.05–1.07) |
0.0604 (0.00493)* |
1.06 (1.05–1.07) |
| -2Log likelihood | 11160.938 | 11048.981 | 11184.497 | 11017.544 | ||||
| SOURCE: Author's calculations using the 1992/1993 look-alike Survey of Income and Program Participaton. | ||||||||
| NOTES: * = standard error significant at the 5 percent level. ** = standard error significant at the 10 percent level. | ||||||||
| n.a. = not applicable. | ||||||||
| a. Ordered logit results. | ||||||||
| b. Reference variable = 1, if self-reported health is excellent. | ||||||||
| c. Reference variable (earn4) = 1, if average relative earnings from ages 45 through 55 are in the 76th–100th percentile of the earnings distribution. | ||||||||
| d. Reference variable = 1, if bachelor's degree or higher. | ||||||||
Self-Reported Health by Age of Retirement, Education, Earnings, and Race
Recall that under the health dichotomy school of thought, if one is able to separate early retirees in extremely poor health (Group A) from all other early retirees (Group C), then the former group should self-report poorer health than age 65 retirees, while the latter group should self-report health no different than age 65 retirees. If one assumes that most of Group A retires at AGE62A, then men retiring at AGE62A should report poorer health than men retiring at AGE65, while men retiring at AGE62B, AGE63, and AGE64 should not. To test this idea, ordered logits are estimated where the dependent variable has five levels of self-reported health—poor, fair, good, very good, and excellent. The logits are set up to predict the log-odds of a man being in a lower (poorer) health category rather than in a higher (better) health category, so that a positive coefficient indicates increased odds of being in poorer health.
Ordered logits predict that men retiring at each retirement age before AGE65 have greater odds of being in a lower health category than men retiring at AGE65 (Table 4, Model 4). Specifically, the odds of being in a lower health category are 87 percent greater at AGE62A, 31 percent greater at AGE62B, 61 percent greater at AGE63, and 36 percent greater at AGE64 relative to men retiring at AGE65. All estimates are statistically significant at the 5 percent level. Although one does not see a uniform decrease in the odds of being in a lower health category with an increase in age of retirement, the small sample size may be contributing large standard errors and imprecise measurement.
| Age of entitlement (retirement age) |
Model 1. Parameter estimate (standard error) |
Model 2. Parameter estimate (standard error) |
Model 3. Parameter estimate (standard error) |
Model 4. | |
|---|---|---|---|---|---|
| Parameter estimate (standard error) |
Odds ratio (confidence interval) |
||||
| AGE62A to AGE64 (reference = AGE65) |
0.4679 (0.0739)* |
n.a. | n.a. | n.a. | n.a. |
| AGE62A to AGE62B (reference = AGE63 to AGE65) |
n.a. | 0.3252 (0.0592)* |
n.a. | n.a. | n.a. |
| AGE62A to AGE62B (reference = AGE65) |
n.a. | n.a. | 0.548 (0.0788)* |
n.a. | n.a. |
| AGE62A (reference = AGE65) |
n.a. | n.a. | n.a. | 0.628 (0.0821)* |
1.87 (1.6–2.2) |
| AGE62B (reference = AGE65) |
n.a. | n.a. | n.a. | 0.2699 (0.112)* |
1.31 (1.05–1.63) |
| AGE63 (reference = AGE65) |
n.a. | n.a. | 0.474 (0.114)* |
0.4759 (0.114)* |
1.61 (1.29–2.01) |
| AGE64 (reference = AGE65) |
n.a. | n.a. | 0.3031 (0.0908)* |
0.3047 (0.0988)* |
1.36 (1.14–1.62) |
| Age at time of health question | 0.0629 (0.0048)* |
0.0633 (0.00482)* |
0.0645 (0.00483)* |
0.0656 (0.00484)* |
1.07 (1.06–1.08) |
| -2Log likelihood | 11227.792 | 11237.906 | 11217.254 | 11205.147 | |
| SOURCE: Author's calculations using the 1973 Exact Match. | |||||
| NOTES: * = standard error significant at the 5 percent level. | |||||
| n.a. = not applicable. | |||||
| a. Ordered logit results. | |||||
These results lend support to the benefits optimization idea, where all early retirees are less healthy or shorter-lived relative to men retiring at the point of unreduced benefits (AGE65). Since the coefficient on AGE62A is almost double the coefficient on AGE64, the group of early retirees entitled to benefits at AGE62A are indeed in the worst health, on average, but those retiring from AGE62B to AGE64 are also in poorer health than those retiring at AGE65.
Because these results suggest that early retirees cannot be divided into a minority in poor health and a majority similar to age 65 retirees, the sensitivity of the correlation between health and age of retirement to different classification schemes that ignore self-selection of retirees at each age before age 65 is checked. Estimates of the odds of being in a lower health category indicate that comparisons of the health of early versus age 65 retirees are sensitive to how the categories are divided. As indicated in Table 4, Models 1–3, the less detailed the retirement-age subdivisions, the less dramatic the difference in health between early and age 65 retirees appears to be. Comparing age 62 retirees with all other retirees appears to create the most distortion, in the sense that the distinguishing characteristics of age 62 retirees are obscured by age 63 and age 64 retirees who get lumped in the reference variable with age 65 retirees. For example, note that the log-odds (parameter estimate) of being in a lower health category drops by almost 50 percent when an age 62 retiree versus all other retiree method of analysis is used instead of an AGE62A versus AGE65 method of analysis (Table 4, Models 2 and 4). Thus, comparing age 62 retirees with all other retirees may be a particularly inappropriate method of analysis to use when creating descriptive statistics of early retirees.
Results also indicate that early retirees are more likely to have lower levels of education and average lifetime earnings than do age 65 retirees. In Table 5, the effects of controlling for those socioeconomic variables on the relationship between self-reported health and age of retirement is examined. The correlation between retirement age and education appears to be stronger than the correlation between retirement age and earnings.
| Variable | Model 1. | Model 2. | Model 3. | Model 4. | Model 5. | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
|
| AGE62A b | 0.628 (0.0821)* |
1.87 (1.6–1.63) |
0.5446 (0.0826)* |
1.7 (1.47–2.03) |
0.3832 (0.0841)* |
1.47 (1.24–1.73) |
0.356 (0.0843)* |
1.43 (1.21–1.68) |
0.3704 (0.0844)* |
1.45 (1.23–1.71) |
| AGE62B b | 0.2699 (0.112)* |
1.31 (1.05–1.63) |
0.1921 (0.1123)** |
1.21 (0.97–1.51) |
0.0113 (0.1136) |
1.01 (0.81–1.26) |
-0.00766 (0.1138) |
0.99 (0.79–1.24) |
0.00904 (0.1139) |
1.01 (0.81–1.26) |
| AGE63 b | 0.4759 (0.114)* |
1.61 (1.29–2.01) |
0.4131 (0.1144)* |
1.51 (1.21–1.89) |
0.3022 (0.1151)* |
1.35 (1.08–1.70) |
0.2785 (0.1153)* |
1.32 (1.05–1.66) |
0.2871 (0.1153)* |
1.33 (1.06–1.67) |
| AGE64 b | 0.3047 (0.0988)* |
1.36 (1.14–1.62) |
0.2245 (0.0913)* |
1.25 (1.05–1.50) |
0.1458 (0.0918) |
1.16 (0.97–1.39) |
0.1124 (0.092) |
1.12 (0.93–1.34) |
0.1229 (0.0921) |
1.13 (0.94–1.35) |
| Earn1 c | n.a. | n.a. | 0.8959 (0.0842)* |
2.45 (2.08–2.89) |
n.a. | n.a. | 0.6233 (0.0866)* |
1.87 (1.57–2.21) |
0.5849 (0.0869)* |
1.80 (1.51–2.13) |
| Earn2 c | n.a. | n.a. | 0.4917 (0.0834)* |
1.64 (1.39–1.93) |
n.a. | n.a. | 0.2982 (0.0849)* |
1.35 (1.14–1.59) |
0.2924 (0.0849)* |
1.34 (1.13–1.58) |
| Earn3 c | n.a. | n.a. | 0.2633 (0.0829)* |
1.30 (1.11–1.53) |
n.a. | n.a. | 0.1895 (0.0833)* |
1.21 (1.03–1.42) |
0.1928 (0.0833)* |
1.21 (1.03–1.43) |
| Edu1 d | n.a. | n.a. | n.a. | n.a. | 1.3334 (0.0888)* |
3.79 (3.19–4.52) |
1.1717 (0.0916)* |
3.23 (2.70–3.86) |
1.1359 (0.0921)* |
3.11 (2.6–3.73) |
| Edu2 d | n.a. | n.a. | n.a. | n.a. | 0.6433 (0.0819)* |
1.90 (1.62–2.23) |
0.5674 (0.083)* |
1.76 (1.50–2.08) |
0.5576 (0.0831)* |
1.75 (1.48–2.1) |
| Black e | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 0.6453 (0.1271)* |
1.91 (1.49–2.45) |
| Age at time of health question | 0.0656 (0.00484)* |
1.07 (1.06–1.08) |
0.0656 (0.00485)* |
1.07 (1.06–1.8) |
0.0538 (0.0049)* |
1.06 (1.05–1.07) |
0.0552 (0.00491) |
1.06 (1.05–1.07) |
0.0568 (0.00493)* |
1.06 (1.05–1.07) |
| -2Log likelihood | 11205.147 | 11083.677 | 10965.31 | 10911.589 | 10887.107 | |||||
| SOURCE: Author's calculations using the 1992/1993 look-alike Survey of Income and Program Participation. | ||||||||||
| NOTES: * = standard error significant at the 5 percent level. ** = standard error significant at the 10 percent level. | ||||||||||
| n.a. = not applicable. | ||||||||||
| a. Ordered logit results. | ||||||||||
| b. Reference variable (AGE65) = 1, if retirement age is greater than or equal to age 65 and less than 66. | ||||||||||
| c. Reference variable (earn4) = 1, if average relative earnings from ages 45 through 55 are in the 76th–100th percentile of the earnings distribution. | ||||||||||
| d. Reference variable = 1, if bachelor's degree or higher. | ||||||||||
| e. Reference variable = 1, if not black. | ||||||||||
There is a 13 percent decrease in the log-odds (parameter estimate) of AGE62A men being in a lower health category relative to AGE65 men when earnings are added and a 39 percent decrease when education is added (Table 5, Models 1, 2, and 3). The drop in the AGE62B and AGE64 coefficients is even larger when education is added; both variables no longer exhibit a significant independent effect on self-reported health (Table 5, Model 3). While AGE64 retains its positive sign when both earnings and education are combined with the retirement-age variables, AGE62B becomes negative (Table 5, Model 4). Thus, the greater odds of self-reporting lower health for AGE62B men appears to be totally explained by the socioeconomic variables; this is not so for AGE62A, AGE63, and perhaps AGE64 men.
Finally, note that in Table 5, Model 5, the odds of being in poorer health are 91 percent greater for black men than for white men, even after controlling for socioeconomic factors. When the effects are decomposed (results not shown), the inclusion of the earnings variables lowers the black coefficient by only 18 percent, the inclusion of the education variables lowers the black coefficient by only 24 percent, and retirement-age variables have virtually no effect on the black coefficient.
Birth Cohort Effects
Although the previous regressions control for age at the time of the health question (which has the same effect as controlling for year of birth), the presence of an age control does not preclude the possibility that the slope of the education and retirement-age effects could still change over time. Interaction effects are tested to see whether the magnitude of education and retirement-age estimates is affected by birth cohort. To adjust for the large movements in the education and retirement-age variables over time, a technique similar to that used in Pappas and others (1993) is adopted whereby a relative measure of educational attainment is created that adjusts for the changing proportions of men in each education category by birth cohort. A relative measure of age at retirement that adjusts for the changing proportions of men in each retirement-age category by birth cohort is also created.9 Each relative measure is then interacted with year of birth (age at time of health question), and log-likelihood tests are conducted to determine whether retirement-age and education differentials change significantly over time. Results (not shown) indicate no significant interactions with year of birth. However, the small sample size could potentially obscure interactions that exist "in nature," and years of birth are not evenly distributed in the sample. For example, men born from 1906 through 1909 make up only 5 percent of the sample, while men born from 1927 through 1930 make up 24 percent of the sample. For these reasons, the interaction test is somewhat weak.
Heterogeneity in Age of Retirement, by Average Lifetime Earnings
So far, the assumption of this section has been that early retirees who are too unhealthy to work but unable to qualify for disability benefits should be clustered at AGE62A. However, the onset of a disabling condition could occur between ages 62 and 64. Thus, it is still possible that a group of individuals in extremely poor health at each early retirement age are driving the results. Because of the widely recognized correlation between lifetime earnings and poor health, average relative lifetime earnings is used as a proxy for health status among men in each retirement-age category.10 The correlation between earnings and health implies that early retirees with earnings in the top quarter of the earnings distribution are the most likely to be equal in health to age 65 retirees and that early retirees with earnings in the bottom quarter of the distribution are the most likely to be in extremely poor health. According to the health dichotomy view of the world, one would expect the lowest earners to report poorer health than age 65 retirees and the highest earners to report health equal to age 65 retirees. If the group of earners in the top quarter of the distribution is more likely to be in poorer health than age 65 retirees, then further doubt is cast on the health dichotomy view of the world.
To attempt to control for heterogeneity within retirement-age categories, AGE62A retirees are divided into four subgroups based on their average relative lifetime earnings—AGE62A and earn1, AGE62A and earn2, AGE62A and earn3, and AGE62A and earn4. Unfortunately, sample size considerations prevent the division of the other subgroups in as detailed a manner. Thus, the other subgroups are measured as follows: AGE62B to AGE63 and earn1, AGE62B to AGE63 and earn2–earn3, AGE62B to AGE63 and earn4, AGE64 and earn1, AGE64 and earn2–earn3, AGE64 and earn4, and AGE65 and earn1. The reference variable is AGE65 and earn2–earn4.
As demonstrated in Table 6, Model 1, all four subgroups of AGE62A have significantly higher odds of being in poorer health than AGE65 (earn2–earn4) retirees. Note that even for men retiring at AGE62A who have average relative lifetime earnings in the top quarter of the earnings distribution, the odds of being in poorer health are increased 35 percent relative to men retiring at age 65 in the top three-fourths of the earnings distribution. Thus, if one thinks of position in the earnings distribution as a proxy for different subgroups of AGE62A retirees, it does not appear that the bottom 25 percent of AGE62A retirees is the only group driving the resulting difference in health between AGE62A retirees and AGE65 retirees. Also of interest is that the log-odds of being in poorer health are 78 percent greater for men retiring at AGE62A in the bottom 25th of the earnings distribution than those for men retiring at AGE62A in the top 25th of the distribution.11 Thus, there is also evidence for a group in extremely poor health clustered at AGE62A and earn1.
| Variable | N | Model 1. | Model 2. | Model 3. | Model 4. | ||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
||
| Retirement-age reference variable | AGE65, earn2 to earn4 | AGE65, earn4 | AGE65, earn1 to earn4 | AGE65, earn2 to earn4 | |||||
| Age at time of health question | 3,818 | 0.066 (0.00486)* |
1.07 (1.06–1.08) |
0.0654 (0.00487)* |
1.07 (1.06–1.08) |
0.0655 (0.00485)* |
1.07 (1.06–1.08) |
0.0571 (0.00494)* |
1.06 (1.05–1.07) |
| AGE62A, earn1 | 419 | 1.3433 (0.116)* |
3.83 (3.05–4.81) |
1.4874 (0.1498)* |
4.43 (3.30–5.94) |
1.2122 (0.1118)* |
3.36 (2.70–4.19) |
0.9386 (0.1194)* |
2.56 (2.02–3.23) |
| AGE62A, earn2 | 362 | 0.7396 (0.1204)* |
2.1 (1.66–2.65) |
0.8812 (0.153)* |
2.41 (1.79–3.26) |
0.61 (0.1165)* |
1.84 (1.47–2.31) |
0.4285 (0.1233)* |
1.54 (1.21–1.95) |
| AGE62A, earn3 | 342 | 0.5818 (0.1226)* |
1.79 (1.41–2.28) |
0.7224 (0.1547)* |
2.06 (1.52–2.79) |
0.4528 (0.1188)* |
1.57 (1.25–1.99) |
0.41 (0.1242)* |
1.51 (1.18–1.92) |
| AGE62A, earn4 | 339 | 0.2966 (0.122)* |
1.35 (1.06–1.71) |
0.4375 (0.1543)* |
1.55 (1.15–2.10) |
0.1687 (0.1183) |
1.18 (0.94–1.49) |
0.1825 (0.123) |
1.20 (0.94–1.53) |
| AGE62B to AGE63, earn1 | 200 | 0.8946 (0.147)* |
2.45 (1.83–3.26) |
n.a. | n.a. | 0.7654 (0.1439)* |
2.15 (1.62–2.85) |
0.509 (0.1503)* |
1.66 (1.24–2.23) |
| AGE62B to AGE63, earn2–earn3 | 386 | 0.5032 (0.1169)* |
1.65 (1.32–2.08) |
n.a. | n.a. | 0.375 (0.113)* |
1.46 (1.17–1.82) |
0.2829 (0.1187)* |
1.33 (1.05–1.68) |
| AGE62B to AGE63, earn4 | 185 | 0.0942 (0.1511) |
1.1 (0.82–1.48) |
n.a. | n.a. | 0.0328 (0.1481) |
0.97 (0.72–1.29) |
0.000531 (0.1518) |
1.00 (0.74–1.35) |
| AGE62B, earn1 | 104 | n.a. | n.a. | 0.9669 (0.2137)* |
2.63 (1.73–4.00) |
n.a. | n.a. | n.a. | n.a. |
| AGE62B, earn2 | 100 | n.a. | n.a. | 0.5391 (0.2163)* |
1.71 (1.12–2.62) |
n.a. | n.a. | n.a. | n.a. |
| AGE62B, earn3 | 95 | n.a. | n.a. | 0.5437 (0.2202)* |
1.72 (1.12–2.65) |
n.a. | n.a. | n.a. | n.a. |
| AGE62B, earn4 | 97 | n.a. | n.a. | 0.0789 (0.2185) |
1.08 (0.71–1.66) |
n.a. | n.a. | n.a. | n.a. |
| AGE63, earn1 | 96 | n.a. | n.a. | 1.1117 (0.2199)* |
3.04 (1.98–4.68) |
n.a. | n.a. | n.a. | n.a. |
| AGE63, earn2 | 93 | n.a. | n.a. | 1.0999 (0.2223)* |
3.00 (1.94–4.64) |
n.a. | n.a. | n.a. | n.a. |
| AGE63, earn3 | 98 | n.a. | n.a. | 0.437 (0.2178)* |
1.55 (1.01–2.37) |
n.a. | n.a. | n.a. | n.a. |
| AGE63, earn4 | 88 | n.a. | n.a. | 0.3848 (0.2263)** |
1.47 (0.94–2.29) |
n.a. | n.a. | n.a. | n.a. |
| AGE64, earn1 | 220 | 0.7146 (0.1417)* |
2.04 (1.55–2.70) |
0.8577 (0.1706)* |
2.36 (1.69–3.29) |
0.5859 (0.1385)* |
1.80 (1.37–2.36) |
0.3667 (0.1441)* |
1.44 (1.09–1.91) |
| AGE64, earn2–earn3 | 416 | 0.5027 (0.1142)* |
1.65 (1.32–2.07) |
n.a. | n.a. | 0.3746 (0.1103)* |
1.45 (1.17–1.81) |
0.3353 (0.1155)* |
1.40 (1.12–1.75) |
| AGE64, earn2 | 212 | n.a. | n.a. | 0.725 (0.1721)* |
2.07 (1.47–2.89) |
n.a. | n.a. | n.a. | n.a. |
| AGE64, earn3 | 204 | n.a. | n.a. | 0.5562 (0.1737)* |
1.74 (1.24–2.45) |
n.a. | n.a. | n.a. | n.a. |
| AGE64, earn4 | 189 | -0.0186 (0.1497) |
0.98 (0.73–1.32) |
0.1222 (0.1771) |
1.13 (0.80–1.60) |
-0.1451 (0.1468) |
0.87 (0.65–1.15) |
-0.051 (0.1504) |
0.95 (0.71–1.28) |
| AGE65, earn1 | 126 | 0.7713 (0.1764)* |
2.16 (1.53–3.06) |
0.9151 (0.2044)* |
2.50 (1.69–3.70) |
n.a. | n.a. | 0.4814 (0.1781)* |
1.62 (1.14–2.30) |
| AGE65, earn2 | 184 | n.a. | n.a. | 0.3932 (0.1786)* |
1.48 (1.04–2.10) |
n.a. | n.a. | n.a. | n.a. |
| AGE65, earn3 | 219 | n.a. | n.a. | 0.0884 (0.1705) |
1.09 (0.78–1.53) |
n.a. | n.a. | n.a. | n.a. |
| Black b | 226 | n.a. | n.a. | n.a. | n,a, | n.a. | n.a. | 0.6544 (0.1272)* |
1.92 (1.50–2.47) |
| Edu1 c | 1,342 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 1.1464 (0.0915)* |
3.15 (2.63–3.77) |
| Edu2 c | 1,755 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 0.5721 (0.0827)* |
1.77 (1.51–2.08) |
| -2Log likelihood | 11086.427 | 11070.988 | 11105.485 | 10884.321 | |||||
| SOURCE: Author's calculations using the 1992/1993 look-alike Survey of Income and Program Participation. | |||||||||
| NOTES: * = standard error significant at the 5 percent level. ** = standard error significant at the 10 percent level. | |||||||||
| n.a. = not applicable. For AGE65 and earn4, n = 231. For variable definitions see text. | |||||||||
| In Model 1, some retirement-age subgroups are combined because of sample size considerations. In Model 2, these subgroups are split apart into greater detail to provide the reader with an additional picture, using a greater level of detail. Results from Model 1 are used to reach the analytical conclusions discussed on pp. 28–30. | |||||||||
| a. Ordered logit results. | |||||||||
| b. Reference variable = 1, if not black. | |||||||||
| c. Reference variable = 1, if bachelor's degree or higher. | |||||||||
Chart 1 illustrates the results. Of the group of men with earnings in the bottom quarter of the earnings distribution, those retiring at AGE62A are the most likely to report poorer health than AGE65 and earn2–earn4 men, followed by a 33 percent decrease in likelihood for men retiring at AGE62B to AGE63. Of men with earn1 earnings, AGE64 and AGE65 men are the least likely to report poorer health compared with men retiring at AGE65 and earn2–earn4, although the likelihood of them doing so is still well above zero. Men in the middle of the earnings distribution (earn2–earn3) show the greatest likelihood of self-reporting poorer health if they retire at AGE62A, while men retiring from AGE62B to AGE64 exhibit a somewhat lower likelihood. Note that early retirees in the middle earnings categories are still more likely to report poorer health than AGE65 retirees, which is further evidence against a poorer health minority. Men in the top quarter of the distribution are the most likely to be in poorer health if they retire at AGE62A, with a 30 percent drop in the log-odds if they retire from AGE62B to AGE63. Only men retiring at AGE64 and earn4 are identical to AGE65 and earn2–earn4 men in the odds of reporting poorer health. Instead of observing a minority of early retirees in poor health and a majority of early retirees with health identical to age 65 retirees as the health dichotomy school proposes, we observe a small minority of early retirees with health indistinguishable from age 65 retirees and an overwhelming majority of early retirees with health poorer than age 65 retirees. This result suggests that early retirees are best described by a combination of the health dichotomy school and the benefits optimization school (the health trichotomy school), with the group that is identical in health to age 65 retirees (Group C) being quite small.
Log-odds of self-reporting a lower health category, by age of retirement subdivided by average lifetime earnings
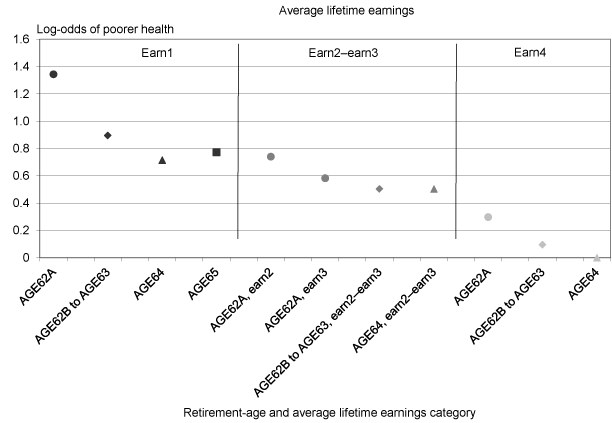
| Retirement-age and average lifetime earnings category | Average lifetime earnings |
|---|---|
| AGE62A, earn1 | 1.3433 |
| AGE62B to AGE63, earn1 | 0.8946 |
| AGE64, earn1 | 0.7146 |
| AGE65, earn1 | 0.7713 |
| AGE62A, earn2 | 0.7396 |
| AGE62A, earn3 | 0.5818 |
| AGE62B TO AGE63, earn2—earn3 | 0.5032 |
| AGE64, earn2—earn3 | 0.5027 |
| AGE62A, earn4 | 0.2966 |
| AGE62B to AGE63, earn4 | 0.0942 |
| AGE64, earn4 | -0.0186 |
The fact that men retiring at AGE65 and earn1 are more likely to self-report poorer health than AGE65 and earn2–earn4 retirees suggests the presence of heterogeneity in the reference variable. This implies that the coefficients on the other retirement-age variables could change with a change in the classification of the reference variable. One way to approach the issue is to create more detailed subgroupings. The downside to this approach is the increase in standard errors that accompanies the decrease in sample size of each individual subgroup of retirees. To create more detailed subgroupings, AGE62B through AGE65 are divided into four separate categories each (one for each earnings category) so that every retirement age is as detailed as AGE62A. As indicated in Table 6, Model 2 and in Chart 2, when AGE65 and earn4 is used as the reference variable, the parameter estimates on the other retirement-age variables generally rise because each subgroup is being compared with what is likely to be the healthiest subgroup in the sample. For example, the coefficient on AGE62A and earn1 increases from 1.3433 to 1.4874 when men retiring at AGE65 with earnings from the 26th to 75th percentile are dropped from the reference variable. Among men retiring at AGE65, those with earnings in the bottom half of the distribution are statistically more likely to self-report a lower health category than men with earnings in the top 25th percentile, while men in the 51st to 75th percentile are not. For men retiring at early ages, those with earnings in the bottom three-fourths of the earnings distribution are always more likely to be in poorer health than are AGE65 and earn4 men, while men retiring at AGE62B and AGE64 with earnings in the top quarter of the earnings distribution are not.
Log-odds of self-reporting a lower health category, by age of retirement subdivided by average lifetime earnings
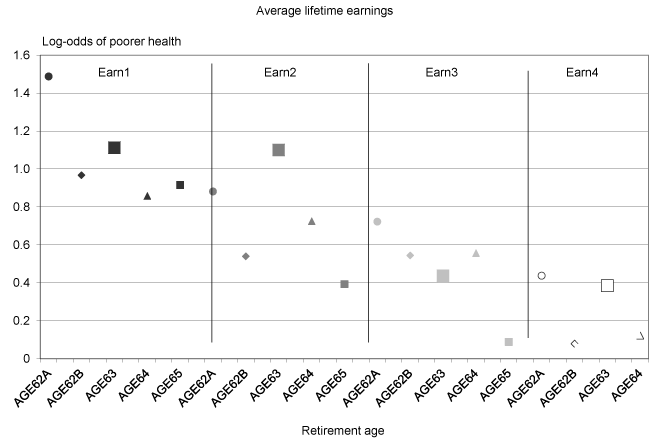
| Retirement age | Average lifetime earnings |
|---|---|
| AGE62A | 1.4874 |
| AGE62B | 0.9669 |
| AGE63 | 1.1117 |
| AGE64 | 0.8577 |
| AGE65 | 0.9151 |
| AGE62A | 0.8812 |
| AGE62B | 0.5391 |
| AGE63 | 1.0999 |
| AGE64 | 0.725 |
| AGE65 | 0.3932 |
| AGE62A | 0.7224 |
| AGE62B | 0.5437 |
| AGE63 | 0.437 |
| AGE64 | 0.5562 |
| AGE65 | 0.0884 |
| AGE62A | 0.4375 |
| AGE62B | 0.0789 |
| AGE63 | 0.3848 |
| AGE64 | 0.1222 |
Another possible approach is to combine all AGE65 retirees into a single reference variable. Because AGE65 retirees with low relative lifetime earnings have relatively poor health in this sample, this has the effect of lowering the coefficients on the other retirement-age variables. For example, the parameter estimate on AGE62A and earn4 retirees falls from 0.2966 to 0.1687 and the odds of this group being in poorer health is no longer statistically different from those of the AGE65 group (Table 6, Model 3). Men in the AGE62B, AGE63, and AGE64 retirement-age groups who have earnings in the top 25th percentile are also no longer statistically different from AGE65 retirees. This is because AGE65 retirees in poorer health (those in the earn1 category) are pulling down the average health of the AGE65 retirees, in another example of how heterogeneity in these retirement-age categories can lead to different interpretations of the same data depending on the categorization adopted.
Further evidence of the effects that heterogeneity among early retirees can create is shown when education and race are controlled for (Table 6, Model 4). When education is added to a regression that already contains retirement-age subcategories divided by earnings level, all the coefficients on the retirement-age variables drop, because of the correlation between education, lifetime relative earnings, and retirement age. The only variable that loses significance in the process (as compared with Table 6, Model 1) is AGE62A and earn4, which is still positive but which drops from 0.2966 to 0.1825. Thus, in this sample, the difference in health between AGE62A and earn4 retirees and AGE65 and earn2–earn4 retirees is explained by differences in educational attainment between the two groups.
Heterogeneity in Age of Retirement, by Receipt and Amount of a Pension Other Than Social Security
Another variable that can be used to measure heterogeneity within age-of-retirement subgroups is receipt of a pension other than Social Security. Theoretically, we would expect having a pension to be positively associated with early retirement and negatively associated with poor health (through the positive association between pension receipt and income or education), so that if we separate early retirees into two groups—those with a pension and those without—we may be able to separate early retirees in poor health from early retirees in good health. According to the benefits optimization school of thought, one would still expect to see early retirees with a pension exhibiting greater odds of being in poorer health than men retiring at AGE65. According to the health dichotomy school of thought, men retiring early with a pension should be indistinguishable from men retiring at AGE65 in terms of the odds of being in poorer health.
Empirically, when logits are estimated where having a pension is the dependent variable, having less than 12 years of education, having earnings in the bottom half of the earnings distribution, and being black make it less likely that a retiree has a pension, while retiring at AGE62A or AGE62B makes it more likely that a retiree has a pension (results not shown). When all of these variables are estimated simultaneously, the correlation between retiring at AGE62A through AGE64 and receipt of a pension becomes larger. Low relative earnings and a low level of educational attainment are both positively correlated with early retirement and negatively correlated with pension receipt. When the negative effects on pension receipt of the lower socioeconomic groups are removed from the early retirement variables, the correlation between early retirement and the likelihood of having a pension rises. Although the negative correlation between race and pension receipt appears to be completely explained by socioeconomic variables, sample size is fairly small (results not shown).
In ordered logits with self-reported health ranging from poor to excellent as the dependent variable, receipt of a pension other than Social Security lowers the log-odds of reporting poorer health by -0.371 (Table 7, Model 1), relative to men without a pension. The size of this coefficient is reduced (to -0.1832) when education and relative earnings are added to the regression, because relatively higher education and higher earnings are positively correlated with pension receipt and negatively correlated with poorer health (Table 7, Model 2). Thus, when one removes the effect of these relatively high education and high earnings groups from the pension variable, the magnitude of its negative correlation with poorer health falls. The pension variable does not appear strongly affected by the inclusion of the retirement-age variables (Table 7, Model 3). The AGE62A coefficient increases with the inclusion of the pension variable (because pension receipt is positively correlated with early retirement and negatively correlated with poor health), but the effect appears slight (Table 7, Model 3 versus Table 5, Model 5).
| Variable | Model 1. Parameter estimate (standard error) |
Model 2. Parameter estimate (standard error) |
Model 3. Parameter estimate (standard error) |
|---|---|---|---|
| Receipt of a pension other than Social Security | -0.371 (0.0628)* |
-0.1832 (0.0654)* |
-0.2078 (0.0659)* |
| Earn1 b | n.a. | 0.505 (0.0931)* |
0.4869 (0.0933)* |
| Earn2 b | n.a. | 0.2331 (0.089)* |
0.236 (0.0891)* |
| Earn3 b | n.a. | 0.1723 (0.0872)* |
0.1816 (0.0872)* |
| Edu1 c | n.a. | 1.2274 (0.0952)* |
1.1614 (0.0973)* |
| Edu2 c | n.a. | 0.6541 (0.0874)* |
0.6022 (0.0886)* |
| Black d | n.a. | 0.5907 (0.1328)* |
0.606 (0.1331)* |
| AGE62A e | n.a. | n.a. | 0.3636 (0.0925)* |
| AGE62B e | n.a. | n.a. | 0.0171 (0.1205) |
| AGE63 e | n.a. | n.a. | 0.2891 (0.1219)* |
| AGE64 e | n.a. | n.a. | 0.106 (0.1006) |
| Age at time of health question | 0.0523 (0.00515)* |
0.0473 (0.00522)* |
0.0544 (0.00549)* |
| -2Log likelihood | 10274.803 | 9986.753 | 9963.416 |
| SOURCE: Author's calculations using the 1992/1993 Survey of Income and Program Participation. | |||
| NOTES: * = standard error significant at the 5 percent level. n.a. = not applicable. For variable definitions, see text. | |||
| a. Ordered logit results. | |||
| b. Reference variable (earn4) = 1, if average relative earnings from ages 45 through 55 are in the 76th–100th percentile of the earnings distribution. | |||
| c. Reference variable = 1, if bachelor's degree or higher. | |||
| d. Reference variable = 1, if not black. | |||
| e. Reference variable (AGE65) = 1, if retirement age is greater than or equal to age 65 and less than 66. | |||
Thus, men who receive a pension are both more likely to retire early and less likely to be in poorer health. One can now test whether men retiring early who receive a pension are any more likely to be in poorer health than men who retire at AGE65. To this end, each retirement-age category (AGE62A to AGE65) is divided into two groups—those who received a pension other than Social Security and those who did not. Because of small sample sizes, AGE62B and AGE63 are combined into one group for estimation.
Results indicate that—regardless of whether they receive a pension other than Social Security or not—men who retire at AGE62A, AGE62B through AGE63, or AGE64 are more likely to self-report a lower health category than all men who retire at AGE65 (Table 8, Model 1). Men retiring early without a pension are also more likely to self-report a lower health category than men retiring early with a pension (Chart 3).
Log-odds of self-reporting a lower health category, by age of retirement subdivided by receipt of a pension other than Social Security
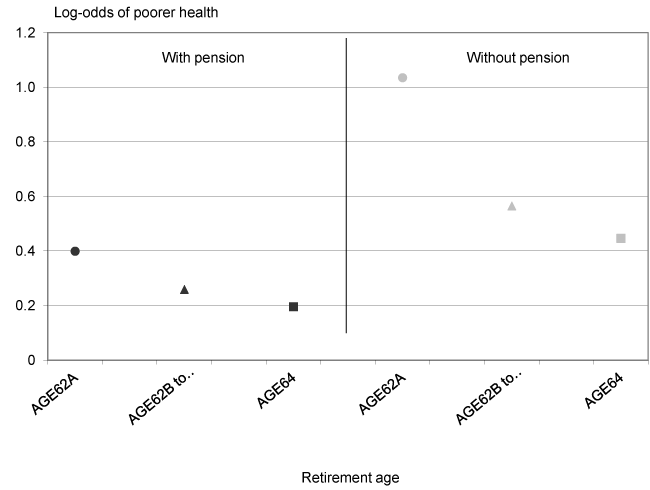
| Retirement age | With pension |
Without pension |
|---|---|---|
| AGE62A | 0.3987 | 1.0346 |
| AGE62B to AGE63 | 0.2586 | 0.5645 |
| AGE64 | 0.1955 | 0.4461 |
| Variable | Model 1. Parameter estimate (standard error) |
Model 2. Parameter estimate (standard error) |
Model 3. Parameter estimate (standard error) |
Model 4. Parameter estimate (standard error) |
|---|---|---|---|---|
| AGE62A, with pension | 0.3987 (0.0961)* |
0.4808 (0.1153)* |
0.2555 (0.1173)* |
0.2648 (0.1174)* |
| AGE62B–AGE63, with pension | 0.2586 (0.1113)* |
0.3405 (0.1281)* |
0.142 (0.1296) |
0.1421 (0.1297) |
| AGE64, with pension | 0.1955 (0.1168)** |
0.2772 (0.1328)* |
0.134 (0.1337) |
0.1241 (0.1297) |
| AGE62A, without pension | 1.0346 (0.1108)* |
1.1169 (0.1278)* |
0.7558 (0.1309)* |
0.6484 (0.1332)* |
| AGE62B–AGE63, without pension | 0.5645 (0.1315)* |
0.6465 (0.1460)* |
0.3507 (0.1482)* |
0.2728 (0.1493)** |
| AGE64, without pension | 0.4461 (0.1250)* |
0.5281 (0.1401)* |
0.2699 (0.1419)** |
0.2085 (0.1426) |
| AGE65, without pension | n.a. | 0.197 (0.1443) |
0.1357 (0.1449) |
0.1139 (0.1451) |
| Edu1 b | n.a. | n.a. | 1.2525 (0.0952)* |
1.1578 (0.0973)* |
| Edu2 b | n.a. | n.a. | 0.6505 (0.0879)* |
0.6066 (0.0887)* |
| Black c | n.a. | n.a. | 0.6705 (0.1322)* |
0.6098 (0.1332)* |
| Earn1 d | n.a. | n.a. | n.a. | 0.4667 (0.0939)* |
| Earn2 d | n.a. | n.a. | n.a. | 0.2255 (0.0892)* |
| Earn3 d | n.a. | n.a. | n.a. | 0.1812 (0.0873)* |
| Age at time of health question | 0.0632 (0.0054)* |
0.0633 (0.00541)* |
0.0537 (0.0055)* |
0.0542 (0.0055)* |
| -2Log likelihood | 10212.368 | 10210.542 | 9987.759 | 9963.051 |
| SOURCE: Author's calculations using the 1992/1993 Survey of Income and Program Participation. | ||||
| NOTES: * = standard error significant at the 5 percent level. ** = standard error significant at the 10 percent level. n.a. = not applicable. For variable definitions see text. | ||||
| a. Ordered logit results. | ||||
| b. Reference variable = 1, if bachelor's degree or higher. | ||||
| c. Reference variable = 1, if not black. | ||||
| d. Reference variable (earn4) = 1, if average relative earnings from ages 45 through 55 are in the 76th–100th percentile of the earnings distribution. | ||||
Thus, early retirees with pensions appear to be in both better health than early retirees without pensions and in worse health than AGE65 retirees. This result tends to contradict the health dichotomy school of thought, because one does not observe that early retirees with pensions are equal in health to age 65 retirees. Although there is no statistical difference in self-reports of health between men retiring at AGE65 with and without a pension, the coefficient on AGE65 and no pension is both positive and lower than the coefficients on any of the early retirement variables (Table 8, Model 2). More importantly, the coefficients on the early retirement variables increase when the reference variable is restricted to AGE65 men with a pension, suggesting the presence of some heterogeneity in the AGE65 population. Lack of statistical significance may be driven by large standard errors resulting from a small sample. With the introduction of socioeconomic variables into the regression, one sees a decrease in all of the early retirement coefficients—due to the strong correlations between socioeconomic variables and early retirement and health. Most of this reduction in magnitude is due to the education variables rather than the earnings variables (Table 8, Models 3 and 4). The variable "AGE62A, with pension" remains significant, while the two variables "AGE62B to AGE63 and AGE64, with pension" are no longer significant but are still positive.
There is also considerable heterogeneity in the level of pension income reported among men who receive a pension. This section explores whether the level of pension income received alters the relationship between pension receipt and self-reported health. This is a way of exploring the question of whether analyses that use receipt of a pension other than Social Security—without examining the level of pension income for each individual—as a tool to analyze early retirees are missing a large degree of heterogeneity in the data.
Because of the wide range of birth cohorts in the sample, if pension income is not adjusted for year of birth, later birth cohorts will have systematically higher pension income because of real earnings growth over time. To achieve this adjustment, birth cohorts in the sample are grouped into four subgroups, and each man's position in the distribution of pension income is calculated for his particular cohort subgroup.12 The variable pension1 includes men with pension income in the bottom 25th percentile of the distribution for their cohort group, pension2 includes men with income in the 26th–50th percentile of the distribution, pension3 includes men in the 51st–75th percentile of the distribution, and pension4 includes men in the 76th–100th percentile of the distribution.
Ordered logits predicting the log-odds of self-reporting poorer health indicate that there is a great deal of heterogeneity in the pension variable. Comparing the estimates in Table 7, Model 1 with the estimates in Table 9, Model 1, one sees that while the log-odds of self-reporting poorer health for men with a pension other than Social Security are -0.371 when men of all levels of pension income are combined into a single variable, the log-odds range from -0.0986 to -0.8528 when the pension variable is split into four subgroups that are based on position in the income distribution. The log-odds of poorer health for men with pension income in the top quarter of the distribution (pension4) is 88 percent lower than those for men with pension income in the bottom quarter of the distribution (pension1). Note that the lower log-odds of being in poorer health for men with a pension relative to men without a pension is only statistically significant for men with income in the top half of the distribution. Controlling for the socioeconomic variables lowers the magnitude of all the pension variables, but it does not alter the qualitative interpretation of the results (Table 9, Model 2). The inclusion of the retirement-age variables does not have a large effect on the pension variables (Table 9, Model 3). Thus, there is strong evidence that a simple dummy variable denoting receipt of a pension other than Social Security will mask a large degree of heterogeneity and could produce misleading analytical conclusions.
| Variable | Model 1. Parameter estimate (standard error) |
Model 2. Parameter estimate (standard error) |
Model 3. Parameter estimate (standard error) |
|---|---|---|---|
| Pension1 b | -0.0986 (0.0922) |
-0.064 (0.0935) |
-0.0664 (0.0937) |
| Pension2 b | -0.1249 (0.0923) |
-0.0155 (0.0951) |
-0.0437 (0.0985) |
| Pension3 b | -0.4373 (0.0925)* |
-0.2464 (0.0953)* |
-0.2854 (0.0962)* |
| Pension4 b | -0.8528 (0.0933)* |
-0.4365 (0.0979)* |
-0.4765 (0.0985)* |
| Earn1 c | n.a. | 0.518 (0.0937)* |
0.4973 (0.094)* |
| Earn2 c | n.a. | 0.212 (0.0895)* |
0.2123 (0.0895)* |
| Earn3 c | n.a. | 0.1606 (0.0873)** |
0.169 (0.0874)** |
| Edu1 d | n.a. | 1.1209 (0.0991)* |
1.0463 (0.1012)* |
| Edu2 d | n.a. | 0.5879 (0.0892)* |
0.5297 (0.0905)* |
| Black e | n.a. | 0.5969 (0.1329)* |
0.6139 (0.1331)* |
| AGE62A | n.a. | n.a. | 0.3751 (0.0927)* |
| AGE62B | n.a. | n.a. | 0.0157 (0.1206) |
| AGE63 | n.a. | n.a. | 0.2785 (0.122)* |
| AGE64 | n.a. | n.a. | 0.0873 (0.1007) |
| Age at time of health question | 0.0514 (0.00516)* |
0.0474 (0.0052)* |
0.0548 (0.00549)* |
| -2Log likelihood | 10214.57 | 9970.479 | 9945.187 |
| SOURCE: Author's calculations using the 1992/1993 Survey of Income and Program Participation. | |||
| NOTES: * = standard error significant at the 5 percent level. ** = standard error significant at the 10 percent level. n.a. = not applicable. For variable definitions see text. | |||
| a. Ordered logit results. | |||
| b. Reference variable = 1, if no pension (other than Social Security). | |||
| c. Reference variable (earn4) = 1, if average relative earnings from ages 45 through 55 are in the 76th–100th percentile of the earnings distribution. | |||
| d. Reference variable = 1, if bachelor's degree or higher. | |||
| e. Reference variable = 1, if not black. | |||
Next, each retirement-age variable is subdivided by level of pension income in Table 10. As shown in previous sections, estimates are sensitive to the level of detail used in the reference variable (AGE65). This is because AGE65 retirees are not homogeneous with regard to health in this sample. If one compares retirees at each age and pension level to all AGE65 retirees, men retiring at any age before 65 with pension income in the bottom 50 percent of the distribution are more likely to be in poorer health than all AGE65 retirees (Table 10, Model 1). Results are somewhat mixed for men retiring early with pension3 income, while men retiring early with pension4 income are not more likely to be in poorer health. If one compares those same retirees with AGE65 retirees with pension income, the coefficients generally rise and AGE62A, pension3 becomes significant (Table 10, Model 2). If one compares those retirees with AGE65 retirees with the highest level of pension income (pension4), the coefficients on the early retirement variables rise again, and only men at pension4 retiring from AGE62A to AGE64 are statistically indistinguishable from men at AGE65, pension4. However, it should be noted that all of the early retirement coefficients are still positive (Table 10, Model 3 and Chart 4).
| Variable | Model 1. Parameter estimate (standard error) |
Model 2. Parameter estimate (standard error) |
Model 3. Parameter estimate (standard error) |
Model 4. Parameter estimate (standard error) |
|---|---|---|---|---|
| Retirement-age variable | AGE65 | AGE65, pension1– pension4 |
AGE65, pension4 |
AGE65, pension4 |
| AGE62A, pension1 | 0.9158 (0.1515)* |
0.9987 (0.1644)* |
1.3562 (0.2128)* |
0.8357 (0.2194)* |
| AGE62A, pension2 | 0.6985 (0.1391)* |
0.7813 (0.153)* |
1.1385 (0.2041)* |
0.6585 (0.2119)* |
| AGE62A, pension3 | 0.2122 (0.1362) |
0.2949 (0.1503)* |
0.6513 (0.2018)* |
0.312 (0.2074) |
| AGE62A, pension4 | -0.1303 (0.1402) |
-0.0477 (0.154) |
0.308 (0.2044) |
0.1033 (0.2074) |
| AGE62B to AGE63, pension1 | 0.5297 (0.1709)* |
0.6124 (0.1823)* |
0.9694 (0.2268)* |
0.4499 (0.2331)** |
| AGE62B to AGE63, pension2 | 0.3705 (0.1798)* |
0.2755 (0.1965) |
0.6321 (0.2383)* |
0.2148 (0.2435) |
| AGE62B to AGE63, pension3 | 0.3705 (0.1798)* |
0.4531 (0.1907)* |
0.8098 (0.2336)* |
0.4692 (0.2381)* |
| AGE62B to AGE63, pension4 | -0.1993 (0.2011) |
-0.1169 (0.2108) |
0.2389 (0.25) |
0.1274 (0.252) |
| AGE64, pension1 | 0.3082 (0.1761)** |
0.3905 (0.1871)* |
0.7475 (0.2306)* |
0.2843 (0.236) |
| AGE64, pension2 | 0.5005 (0.1969)* |
0.5829 (0.2068)* |
0.9403 (0.2469)* |
0.5702 (0.2505)* |
| AGE64, pension3 | 0.0458 (0.2165) |
0.1281 (0.2255) |
0.4846 (0.2627)** |
0.1558 (0.266) |
| AGE64, pension4 | -0.2512 (0.2131) |
-0.1689 (0.2223) |
0.1869 (0.2598) |
0.1623 (0.2611) |
| AGE65, pension1 | n.a. | n.a. | 0.3935 (0.2626) |
0.0766 (0.2665) |
| AGE65, pension2 | n.a. | n.a. | 0.7515 (0.2598)* |
0.5294 (0.263)* |
| AGE65, pension3 | n.a. | n.a. | 0.4136 (0.2616) |
0.1375 (0.2649) |
| AGE62A, without pension | 1.0396 (0.1109)* |
1.1225 (0.128)* |
1.4803 (0.1862)* |
0.8523 (0.1941)* |
| AGE62B to AGE 63, without pension | 0.5675 (0.1317)* |
0.6501 (0.1462)* |
1.0074 (0.1989)* |
0.4717 (0.205)* |
| AGE64, without pension | 0.4479 (0.1251)* |
0.5304 (0.1403)* |
0.8875 (0.1946)* |
0.4034 (0.2)* |
| AGE65, without pension | n.a. | 0.1985 (0.1445) |
0.5552 (0.1975)* |
0.2939 (0.2) |
| Edu1 b | n.a. | n.a. | n.a. | 1.0533 (0.1015)* |
| Edu2 b | n.a. | n.a. | n.a. | 0.5497 (0.0909)* |
| Black c | n.a. | n.a. | n.a. | 0.6206 (0.1334)* |
| Earn1 d | n.a. | n.a. | n.a. | 0.4694 (0.0947)* |
| Earn2 d | n.a. | n.a. | n.a. | 0.1912 (0.0899)* |
| Earn3 d | n.a. | n.a. | n.a. | 0.1598 (0.0876)** |
| Age at time of health question | 0.0625 (0.00541)* |
0.0626 (0.00541)* |
0.0626 (0.00542)* |
0.0548 (0.00551)* |
| -2Log likelihood | 10149.389 | 10147.546 | 10138.543 | 9932.097 |
| SOURCE: Author's calculations using the 1992/1993 Survey of Income and Program Participation. | ||||
| NOTES: * = standard error significant at the 5 percent level. ** = standard error significant at the 10 percent level. | ||||
| n.a. = not applicable. | ||||
| For variable definitions see text. | ||||
| a. Ordered logit results. | ||||
| b. Reference variable = 1, if bachelor's degree or higher. | ||||
| c. Reference variable = 1, if not black. | ||||
| d. Reference variable (earn4) = 1, if average relative earnings from ages 45 through 55 are in the 76th–100th percentile of the earnings distribution. | ||||
Log-odds of self-reporting a lower health category, by age of retirement subdivided by level of non-Social Security pension income
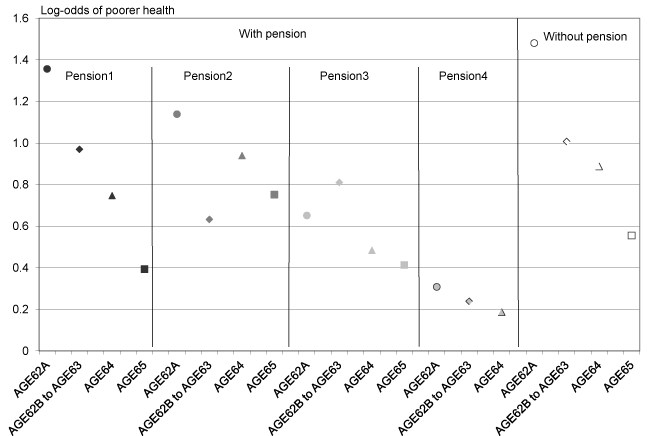
| Retirement age | Pension 1 | Pension 2 | Pension 3 | Pension 4 | Without pension |
|---|---|---|---|---|---|
| AGE62A | 1.3562 | 1.1385 | 0.6513 | 0.308 | 1.4803 |
| AGE62B to AGE63 | 0.9694 | 0.6321 | 0.8098 | 0.2389 | 1.0074 |
| AGE64 | 0.7475 | 0.9403 | 0.4846 | 0.1869 | 0.8875 |
| AGE65 | 0.3935 | 0.7515 | 0.4136 | . . . | 0.5552 |
| NOTE: . . . = not applicable. | |||||
The inclusion of socioeconomic variables lowers the magnitude of the retirement-age coefficients, but the qualitative results are unchanged (Table 10, Model 4). Thus, results indicate that when classifying early retirees by level of pension income, only men retiring before age 65 who are in the top half or top quarter of the pension income distribution (depending on the reference variable used) have health equal to that of age 65 retirees. These results suggest early retirees are best described by a health trichotomy school of thought that consists of Group A—early retirees in extremely poor health; Group C—retirees with health equal to age 65 retirees; and Group B—those with health in between Groups A and C; and that Group C, early retirees with health equal to age 65 retirees, is a small minority rather than a majority.
Empirical Results on Mortality Using Matched CPS/SSA Data
While health and mortality are used interchangeably in this paper to expound on the three views of early retirees, it should be noted that mortality can be a more all-encompassing measure. For example, an individual may self-report good health but know that all of the men in his family have died young, and retire at the earliest opportunity. Thus, an advantage of using mortality over health as a way to categorize early retirees is that the timing of one's death includes genetic, behavioral, and environmental factors that may not be observed on a health survey. In addition, some researchers have questioned the objectiveness of self-reported health. For example, Bazzoli (1985, 232) argues that the effect of health on retirement is overstated because survey respondents overstate poor health to provide a socially acceptable reason for retirement. Self-reported health may also be subjective in that what one individual perceives as fair health another individual may perceive as poor health. In these ways, mortality analysis provides a less ambiguous way of evaluating heterogeneity among retirees, because its objectivity cannot be questioned and its outcome is final. This section uses differences in mortality risk to describe early retirees to both complement and check the results of the previous health section with an objective measure. In addition, it checks the qualitative conclusions drawn using the 1992/1993 SIPP analysis with a sample that is more than double its size.
Data Description
The use of Social Security's longitudinal administrative data matched to the Bureau of the Census' 1973 Current Population Survey (referred to as the 1973 Exact Match) for mortality research builds on previous work with the data set by Duleep (1986, 1989). Links between earnings, age of retirement, and mortality were first explored by Wolfson and others (1993) using Canadian administrative data.13 This study uses a version of the 1973 Exact Match in which the matched Social Security administrative data have been updated by Bert Kestenbaum and Chris Chaplain, in SSA's Office of the Chief Actuary, to include beneficiary and claim data from the date of the respondent's entitlement up to mid-1998 (Master Beneficiary Records (MBR)) and death data (Numident, MBR, and Master Earnings File). As in the previous analysis, the subsample used for analysis consists of male, retired-worker beneficiaries, excluding individuals who have ever received Social Security Disability Insurance. And to ensure that all men have an equal chance of claiming benefits at age 62 through age 65 in the sample, all men who die before age 66 are eliminated.14
The model used to estimate the variables described below is a discrete-time logistic regression.15 Observations begin in the year the worker turns age 65 and end in the earlier of either the year of death or the end of the observation period (1997). The dependent variable is equal to 1 in the year the worker dies and 0 in every year the worker survives. Counting all annual observations for the 9,054 workers in the sample, there are 3,438 person-years in which a worker died and 90,565 person-years in which a worker survived for a total of 94,003 pooled observations. The model measures the logit or log-odds of dying on those 94,003 pooled observations using the maximum likelihood method of estimation. Regressions performed here use unweighted data. A summary of the sample used for this analysis is given in Table 11.
| Category | Unweighted count |
|---|---|
| Male retired-worker beneficiaries— | |
| Born from 1908 through 1931 | 10,052 |
| Minus those entitled at age 66 or older | 9,758 |
| Surviving to at least age 66 | 9,412 |
| With some nonzero earnings from ages 45 through 55 | 9,054 |
| Pooled observations | 94,003 |
| SOURCE: Author's tabulations using the 1973 Exact Match. | |
Explanatory Variables
The following section defines the variables used in the mortality analysis portion of the paper. There is no measure of pension receipt in the 1973 Exact Match. Thus, only the analysis of the 1992/1993 SIPP (discussed earlier in the health section of the paper) considers pension receipt.
Current Age. Current age from age 65 to death or through year 1997 (for a maximum age of 89 for a worker who is born in 1908) is used to estimate the effect of age on mortality risk. Current age is a censored, time-varying variable because the measurement of current age ends in 1997 (the end of the observation period). Therefore, censoring increases with birth cohort.
Year of Birth. Because mortality has improved over time, a continuous year-of-birth variable is used to estimate an independent cohort or period effect on mortality risk. This variable is observed in SSA's administrative data.
Marital Status. Marital status in 1973 is used to approximate a measure of the effect of marriage on mortality risk. This variable does not have the explanatory power of a marriage variable, like current marital status, that changes over time; however, the data file provides only a point-in-time measure of marriage.16 This variable is observed in the 1973 CPS.
Race. Race data in the 1973 Exact Match includes only the categories white, black, and other. Estimates are made for the effect of being black on mortality risk. This variable is observed in the 1973 CPS.
Education. Education, recorded in the CPS in single years, is grouped into three categories for estimation: less than 12 years of school—less than high school (edu1), 12–15 years of school—high school graduate (edu2), and 16 or more years of school—college graduate (edu3). This variable is observed in the 1973 CPS.
Earnings. Earnings are measured exactly as described in the previous section on health using the matched SIPP/SSA data.
Retirement Age. The retirement-age variables are measured exactly as described in the previous section on health using the matched SIPP/SSA data.
Preliminary Statistics
In this section, the distribution of the sample by some of the explanatory variables is examined (see Table 12). The last column in the table gives the estimated probability that an individual will survive until age 80 or older for each subgroup, given survival to age 66. The survival estimates are obtained using the life-table (actuarial) method.17 For the full sample, given survival to age 66, there is a 69 percent probability that an individual will survive until age 80 or older. When examining survival probabilities for various subsamples, several patterns emerge. Survival probability increases with education, earnings percentile, and age of retirement. There is a 7 percentage-point difference between those with less than 12 years of education and those with at least 16 years of education, a 6 percentage-point difference between those in the bottom earnings percentile and those in the top earnings percentile, and an 11 percentage-point difference between AGE62A retirees and AGE65 retirees. As shown in Table 13, earnings are fairly evenly distributed within retirement-age categories—with the exception of AGE62A retirees who have a higher proportion of men in the bottom quarter of the earnings distribution and AGE65 retirees who have a higher proportion of men in the top quarter of the earnings distribution. Note that AGE65 retirees also have the lowest proportion of men in the lowest education category and the highest proportion of men in the highest education category.
| Variable | Number | Percentage of sample |
Survival probability to age 80 |
|---|---|---|---|
| Full sample | 9,054 | 100.0 | 0.69 |
| Education (years) | |||
| Less than 12 | 3,543 | 39.1 | 0.66 |
| 12–15 | 4,085 | 45.1 | 0.71 |
| 16 or more | 1,426 | 15.8 | 0.73 |
| Earnings (percentiles) | |||
| 0–25th | 2,272 | 25.1 | 0.66 |
| 26th–50th | 2,261 | 25.0 | 0.69 |
| 51st–75th | 2,268 | 25.1 | 0.70 |
| 76th–100th | 2,253 | 25.0 | 0.72 |
| Marital status in 1973 | |||
| Married | 8,133 | 89.8 | 0.70 |
| Not married | 921 | 10.2 | 0.62 |
| Retirement age | |||
| AGE62A | 3,494 | 38.6 | 0.64 |
| AGE62B | 988 | 10.9 | 0.68 |
| AGE63 | 933 | 10.3 | 0.69 |
| AGE64 | 1,888 | 20.9 | 0.71 |
| AGE65 | 1,751 | 19.3 | 0.75 |
| Race | |||
| Black | 513 | 5.7 | 0.63 |
| White | 8,541 | 93.4 | 0.69 |
| SOURCE: Author's calculations using the 1973 Exact Match. | |||
| Variable | Full sample |
AGE62A | AGE62B | AGE63 | AGE64 | AGE65 |
|---|---|---|---|---|---|---|
| Education (years) | ||||||
| Less than 12 | 39.1 | 42.0 | 44.1 | 39.0 | 39.0 | 29.7 |
| 12–15 | 45.1 | 46.1 | 44.1 | 45.4 | 45.5 | 43.1 |
| 16 or more | 15.8 | 11.9 | 11.7 | 13.5 | 15.5 | 27.2 |
| Earnings (percentiles) | ||||||
| 0–25th | 25.1 | 30.3 | 23.9 | 25.8 | 23.7 | 16.0 |
| 26th–50th | 25.0 | 23.9 | 25.8 | 25.3 | 30.2 | 20.9 |
| 51st–75th | 25.1 | 23.6 | 26.9 | 23.7 | 24.5 | 28.0 |
| 76th–100th | 25.0 | 22.3 | 23.4 | 25.2 | 21.6 | 35.1 |
| SOURCE: Author's calculations using the 1973 Exact Match. | ||||||
Mortality Risk, by Age of Retirement, Education, and Earnings
Recall that, according to the health dichotomy school of thought, one expects early retirees who are too unhealthy to work but are unable to qualify for disability benefits to claim benefits as soon as they possibly can. Under that assumption, one might expect that, on average, men claiming benefits at AGE62A should have higher mortality risk than those claiming benefits at AGE65, while men claiming benefits at AGE62B to AGE64 should not. Under the benefits optimization school of thought, men claiming benefits at each age before age 65 should have higher mortality risk than AGE65 men. Waldron (2001, 2002) found that men retiring at each retirement age before AGE65 exhibited significantly higher mortality risk than did AGE65 men, which tends to support the benefits optimization idea. Relative mortality risk estimates in Waldron (2001, 2002) controlled for current age, year of birth, education, marital status at a point in time, and race. However, the preliminary statistics in this paper indicate that not only do early retirees have a lower proportion of higher educated men than do age 65 retirees, they also have a lower proportion of men with high average lifetime earnings than do age 65 retirees. Since earnings levels are expected to be positively correlated with survival, differences in survival probability to age 80 between early and late retirees could result from differences in average relative earnings between the two groups. If differences in survival probability between early and late retirees remain after controlling for both education and lifetime earnings, then one can conclude that there is some residual difference in mortality risk factors between the two groups not explained by either of these socioeconomic factors.
Regression results in this paper for the retirement-age variables follow the same pattern as the life-table estimates of survival probability by retirement age reported previously. Mortality risk decreases with an increase in the age at which an individual in the sample retires, even when controlling for current age, year of birth, marital status, education, average relative earnings, and race—thus suggesting an independent relationship between retirement age and mortality risk (Table 14).
In Table 14, retiring at AGE62A increases the log-odds of dying (parameter estimate) by 0.2861 relative to those retiring at AGE65, holding all the other variables constant. Relative to those retiring at AGE65, retiring at AGE62B increases the log-odds of dying by 0.1843; retiring at AGE63 increases the log-odds by 0.1472; and retiring at AGE64 increases the log-odds of dying by 0.0942. All explanatory variables are significant at the 5 percent level, except for AGE64, which is significant at the 10 percent level.
| Variable | Parameter estimate (standard error) |
Odds ratio (confidence Interval) |
|---|---|---|
| Intercept | 10.5382 (7.362) |
n.a. |
| AGE62A b | 0.2861 (0.0512)* |
1.33 (1.20–1.47) |
| AGE62B b | 0.1843 (0.0674)* |
1.20 (1.05–1.37) |
| AGE63 b | 0.1472 (0.0663)* |
1.16 (1.02–1.32) |
| AGE64 b | 0.0942 (0.0556)** |
1.10 (0.99–1.23) |
| Earn1 c | 0.1737 (0.0523)* |
1.19 (1.07–1.32) |
| Earn2 c | 0.0718 (0.0518) |
1.07 (0.97–1.19) |
| Earn3 c | 0.1057 (0.0513)* |
1.11 (1.01–1.23) |
| Edu1 d | 0.3006 (0.0617)* |
1.35 (1.20–1.52) |
| Edu2 d | 0.1419 (0.061)* |
1.15 (1.02–1.30) |
| Black e | 0.1715 (0.073)* |
1.19 (1.03–1.37) |
| Age | 0.1047 (0.00348)* |
1.11 (1.10–1.12) |
| Year of birth | -0.113 (0.00378)* |
0.99 (0.98–1.00) |
| Married in 1973 f | -0.254 (0.0535)* |
0.78 (0.70–0.86) |
| -2Log likelihood | 28061.685 | |
| SOURCE: Author's calculations using the 1973 Exact Match. | ||
| NOTES: * = standard error significant at the 5 percent level. ** = standard error significant at the 10 percent level. n.a. = not applicable. | ||
| a. Logistic regression results. | ||
| b. Reference variable (AGE65) = 1, if retirement age is greater than age 65 and less than 66. | ||
| c. Reference variable (earn4) = 1, if average relative earnings from ages 45 through 55 are in the 76th–100th percentile of the earnings distribution. | ||
| d. Reference variable (edu3) = 1, if 16 or more years of school. | ||
| e. Reference variable = 1, if not black. | ||
| f. Reference variable = 1, if not married in 1973. | ||
Note that having less than 12 years of education increases the odds of dying by 35 percent relative to men with 16 or more years of education and that retiring at AGE62A increases the odds of dying by 33 percent relative to AGE65, so that in terms of magnitude, the relative odds of dying appear similar for these two variables. In addition, there is a 20 percent increase in the odds of dying for men retiring at AGE62B, relative to men retiring at AGE65; a 16 percent increase for men retiring at AGE63; and a 10 percent increase for men retiring at AGE64.18
These results differ somewhat from the preceding health section in which the AGE62B and AGE64 no longer exhibit a significant independent effect on self-reported health when controlling for socioeconomic variables (Table 5, Model 3). Since the sample used for the mortality analysis (the 1973 Exact Match) is more than double the size of the sample used for the health analysis presented earlier using the 1992/1993 SIPP, 3,800 records from the 1973 Exact Match are randomly sampled to match the size of the 1992/1993 look-alike SIPP. In regressions performed on 20 different random draws of the 1973 Exact Match, AGE62A always exhibits a statistically independent effect on the log-odds of dying; AGE62B is significant 50 percent of the time; AGE63 is significant 40 percent of the time; and AGE64 is significant 20 percent of the time, relative to AGE65 when controlling for socioeconomic effects. From this result one can conclude that while the relationship—after controlling for socioeconomic effects—between retirement age and mortality appears stronger than the relationship between retirement age and self-reported health, that perception is driven by sample size differences. A definitive answer to the question of whether the retirement ages other than AGE62A hold their correlation with self-reported health after socioeconomic variables are controlled for requires a larger sample than the one used in this paper.
Because of the complexity of implementation or a lack of data availability, many models that include socioeconomic differences in mortality when evaluating Social Security–related issues choose to stratify by only one variable—usually either education or earnings. Thus, it is useful to compare the strength of the earnings variables in relation to the education variables. An examination of the earnings and education coefficients in Table 15 suggests that while each socioeconomic variable is stronger in the absence of another, on average, the education variables exhibit slightly more power than the earnings variables. In other words, the inclusion of the education variables decreases the earnings coefficients by more than the inclusion of the earnings variables decreases the education coefficients. Note that this result holds even when the earnings percentiles are disaggregated at increments smaller than the percentiles reported here. In particular, earn2 (earnings in the 26th–50th percentile) becomes insignificant when education dummies are introduced. This suggests the presence of some collinearity between education and earnings. Education variables also exhibit slightly more power than the earnings variables in relation to the effect of their inclusion in a regression on the retirement-age variables in Tables 16. (However, as explained in footnote 7, the greater power of education variables could be related to better data quality rather than a reflection of qualitative differences in meaning between the two socioeconomic measures.) Also, note that the inclusion of retirement-age variables in Table 16 lowers the education coefficients and earnings coefficients relative to Table 15.
| Variable | Earnings | Education | Earnings and education | |||
|---|---|---|---|---|---|---|
| Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
|
| Earn1 b | 0.2778 (0.0507)* |
1.32 (1.20–1.46) |
n.a. | n.a. | 0.2034 (0.052)* |
1.23 (1.11–1.36) |
| Earn2 b | 0.1297 (0.051)* |
1.14 (1.03–1.26) |
n.a. | n.a. | 0.0796 (0.0516) |
1.08 (0.98–1.20) |
| Earn3 b | 0.1208 (0.0512)* |
1.13 (1.02–1.25) |
n.a. | n.a. | 0.1067 (0.0513)* |
1.11 (1.01–1.23) |
| Edu1 c | n.a. | n.a. | 0.3946 (0.0596)* |
1.48 (1.32–1.67) |
0.3544 (0.0609)* |
1.43 (1.27–1.61) |
| Edu2 c | n.a. | n.a. | 0.1947 (0.0603)* |
1.22 (1.08–1.37) |
0.1797 (0.0605)* |
1.20 (1.06–1.35) |
| -2Log likelihood | 28139.265 | 28113.255 | 28097.301 | |||
| SOURCE: Author's calculations using the 1973 Exact Match. | ||||||
| NOTES: * = standard error significant at the 5 percent level. | ||||||
| All regressions control for these variables—age, year of birth, married in 1973, and black (coefficients not shown). | ||||||
| n.a. = not applicable. | ||||||
| a. Logistic regression results. | ||||||
| b. Reference variable (earn4) = 1, if average relative earnings from ages 45 through 55 are in the 76th–100th percentile of the earnings distribution. | ||||||
| c. Reference variable (edu3) = 1, if 16 or more years of school. | ||||||
| Variable | Retirement age | Retirement age and earnings |
Retirement age and education |
|||
|---|---|---|---|---|---|---|
| Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
Parameter estimate (standard error) |
Odds ratio (confidence interval) |
|
| AGE62A b | 0.3586 (0.05)* |
1.43 (1.30–1.58) |
0.3281 (0.0506)* |
1.39 (1.26–1.53) |
0.302 (0.0509)* |
1.35 (1.22–1.50) |
| AGE62B b | 0.2531 (0.0666)* |
1.29 (1.13–1.47) |
0.2317 (0.0668)* |
1.26 (1.11–1.44) |
0.1939 (0.0673)* |
1.21 (1.06–1.39) |
| AGE63 b | 0.2054 (0.0657)* |
1.23 (1.08–1.40) |
0.1817 (0.0659)* |
1.20 (1.05–1.37) |
0.1588 (0.0661)* |
1.17 (1.03–1.33) |
| AGE64 b | 0.1417 (0.055)* |
1.15 (1.04–1.28) |
0.1227 (0.0553)* |
1.13 (1.01–1.26) |
0.1032 (0.0554)** |
1.11 (1.00–1.24) |
| Earn1 c | n.a. | n.a. | 0.2315 (0.0512)* |
1.26 (1.14–1.39) |
n.a. | n.a. |
| Earn2 c | n.a. | n.a. | 0.1104 (0.0513)* |
1.12 (1.01–1.24) |
n.a. | n.a. |
| Earn3 c | n.a. | n.a. | 0.1168 (0.0512)* |
1.12 (1.02–1.24) |
n.a. | n.a. |
| Edu1 d | n.a. | n.a. | n.a. | n.a. | 0.2398 (0.0607)* |
1.39 (1.24–1.57) |
| Edu2 d | n.a. | n.a. | n.a. | n.a. | 0.1513 (0.0609)* |
1.16 (1.03–1.31) |
| -2Log likelihood | 28112.88 | 28092.283 | 28073.423 | |||
| SOURCE: Author's calculations using the 1973 Exact Match. | ||||||
| NOTES: * = standard error significant at the 5 percent level. ** = standard error significant at the 10 percent level. | ||||||
| All regressions control for these variables—age, year of birth, married in 1973, and black (coefficients not shown). | ||||||
| n.a. = not applicable. | ||||||
| a. Logistic regression results. | ||||||
| b. Reference variable (AGE65) = 1, if retirement age is greater than age 65 and less than 66. | ||||||
| c. Reference variable (earn4) = 1, if average relative earnings from ages 45 through 55 are in the 76th–100th percentile of the earnings distribution. | ||||||
| d. Reference variable (edu3) = 1, if 16 or more years of school. | ||||||
Thus, all three of these variables—education, earnings, and retirement age—tend to pick up some of the effects of whichever variable is absent. However, no one variable appears to be a pure proxy for the other, in that when all three variables are combined in a single regression (Table 14), each explanatory variable retains a separate explanatory power (with the exception of earn2). This phenomenon suggests a greater cumulative distance in adverse mortality risk between the most at-risk subgroup and the least at-risk subgroup than would be the case if only one variable is chosen to proxy for a subgroup's differential. Table 17 illustrates this cumulative effect by converting the mortality differentials of Tables 14–16 into differences in life expectancy at age 65. Combining all three variables, as opposed to using one single variable, adds anywhere from 2 years and 10 months to 3 years and 7 months difference in life expectancy between hypothetical Male A and Male B (see Table 17).
| Subgroup | Education differentials only |
Earnings differentials only |
Retirement-age differentials only | Education, earnings, and retirement-age differentials |
|---|---|---|---|---|
| Male A a | 81.1 | 82 | 82.2 | 80 |
| Male B b | 84 | 84.1 | 84.9 | 85.7 |
| Difference in life expectancy between Male A and Male B | 2.9 | 2.1 | 2.7 | 5.7 |
| SOURCE: Author's calculations using the 1973 Exact Match. | ||||
| NOTE: Life expectancy (in years) by various mortality differentials are measured at age 65 for hypothetical white, married men born in 1930. | ||||
| a. Male A has less than 12 years of school, average earnings in the 0–25th percentile of the earnings distribution, and retired at AGE62A. | ||||
| b. Male B has 16 or more years of school, average earnings in the 75th–100th percentile of the earnings distribtion, and retired at AGE65. | ||||
Birth Cohort Effects
Although the previous estimates control for year of birth, they do not measure whether the slopes of the education and retirement-age mortality differentials change over time. As in the previous analysis of health, interaction effects are tested to see whether the magnitude of the education and retirement-age estimates is affected by birth cohort. Age is also separately interacted with education, earnings, retirement age, and marital status in 1973 to see whether these mortality differentials narrow with its inclusion.
In Waldron (2001)—where the regressions lacked an earnings measure—results indicated that education, retirement, and marriage mortality differentials tend to narrow with age. Once earnings are included in a multivariate regression, differentials still appear to narrow somewhat with age, but only the marriage interaction is still strong enough to be statistically significant (results not shown).
Similar to Preston and Elo (1995), who found that education differentials have widened from 1960 to 1979–1985, when controlling for the change in the percentile of the population at each education level, education differentials widen from birth cohort 1908 to birth cohort 1931 in the 1973 Exact Match (results not shown). However, the magnitude of the retirement-age coefficients is not affected by the inclusion of an interaction between the education index and birth cohort. A statistically significant widening of the retirement-age differentials over time is not found.
The increase in mortality differentials by education over time is noteworthy and may have implications for proposals to link Social Security's full retirement age to increases in average longevity (proposals include: Reform Model 3—President's Commission to Strengthen Social Security (2001); National Commission on Retirement Policy (1999); and Option II—Report of the 1994–1996 Advisory Council on Social Security (1997)). For an increase in the full retirement age linked to increases in average longevity to be distributionally neutral, longevity improvement would have to proceed at the same rate for different population subgroups. However, in the simplified example in Table 18, men born in 1908 with less than 12 years of education were only 0.3 years below average life expectancy, while those born in the 1928 birth cohort were 1.7 years below average life expectancy. This widening divergence from average life expectancy reflects both the shrinking proportion of men in the lowest education group and the widening differential by education level net of the shifting proportions of men in each education category. If these population subgroups do not experience mortality gains at the same rate in the future, the longer-lived could dominate "average improvements" to a greater degree than shorter-lived individuals. This would imply that linking the full retirement age to improvements in average longevity could have differential effects over time. Clearly, further investigation of this interaction is warranted.19
| Educational attainment (in years) | 1908 | 1913 | 1918 | 1923 | 1928 |
|---|---|---|---|---|---|
| Life expectancy at age 65 | |||||
| Less than 12 | 79.6 | 79.8 | 80.0 | 80.2 | 80.3 |
| 12–15 | 79.9 | 80.6 | 81.2 | 81.9 | 82.5 |
| 16 or more | 81.2 | 81.7 | 82.2 | 82.7 | 83.2 |
| Average life expectancy a | 79.9 | 80.3 | 80.9 | 81.5 | 82.0 |
| Differences in average life expectancy | |||||
| Less than 12 | -0.3 | -0.5 | -0.9 | -1.3 | -1.7 |
| 12–15 | 0 | 0.3 | 0.3 | 0.4 | 0.5 |
| 16 or more | 1.3 | 1.4 | 1.3 | 1.2 | 1.2 |
| SOURCE: Author's calculations using the 1973 Exact Match. | |||||
| NOTE: Life expectancy (in years) estimated for white, married men retiring at age 62A with earnings in the 26th–50th percentile of the earnings distribution. | |||||
| a. The average is weighted by the proportion of the selected birth cohort in each education category. | |||||
Heterogeneity in the Age-of-Retirement Variables, by Average Lifetime Earnings
So far the assumption of this section has been that early retirees who are too unhealthy to work but unable to qualify for disability benefits should be clustered at AGE62A. However, the onset of a disabling condition could occur at ages 62–64. Thus, it is still possible that a group of individuals in extremely poor health at each early retirement age are driving the results. To attempt to control for heterogeneity within retirement-age categories, the age-of-retirement variables are subdivided by four average relative lifetime earnings categories.
Specifically, AGE62A retirees are divided into four subgroups based on their average relative lifetime earnings—AGE62A and earn1, AGE62A and earn2, AGE62A and earn3, and AGE62A and earn4. Unfortunately, sample size considerations prevent the division of the other subgroups in as detailed a manner. Thus, the other subgroups are measured as follows: AGE62B to AGE63 and earn1, AGE62B to AGE63 and earn2–earn3, AGE62B to AGE63 and earn4, AGE64 and earn1, AGE64 and earn2–earn3, AGE64 and earn4, and AGE65 and earn1. The reference variable is AGE65 and earn2–earn4. Because having low lifetime earnings is correlated with higher mortality risk, one might expect that men retiring early with earnings in the bottom quarter of the earnings distribution would die sooner than AGE65 retirees, while men retiring early with earnings in the top quarter of the earnings distribution would not. Such a result would tend to support the health dichotomy school of thought. On the other hand, if high-earning men who retire early do not live as long as men who retire at the normal retirement age, the benefits optimization school of thought may provide a better description of the population. If the data reveals a group of early retirees with high mortality risk, a group in the middle, and a group with mortality risk equal to that of AGE65 retirees, then the population may be best described as a combination of both schools of thought (a health trichotomy).
As illustrated in Table 19, all four subgroups of AGE62A are associated with significantly higher mortality risk than AGE65. Note that even for men retiring at AGE62A who have average relative lifetime earnings in the top quarter of the earnings distribution, the odds of dying are 27 percent greater than those for men retiring at age 65. Thus, if one thinks of position in the earnings distribution as a proxy for different subgroups of age 62 retirees, it does not appear that the bottom 25 percent of age 62 retirees are driving the resulting difference in mortality risk between age 62 retirees and age 65 retirees. Instead, as Chart 5 indicates, the positive correlation between longevity and retirement age generally holds, even when subdividing retirement-age categories by average relative lifetime earnings. Note that AGE64 retirees seem the most heterogeneous, in that AGE64 and earn1 retirees have an estimated life expectancy most similar to AGE62A retirees, and AGE64 and earn4 retirees have an estimated life expectancy most similar to AGE65 retirees. AGE65 and earn1 retirees are indistinguishable from other AGE65 retirees, but sample size is also small for the former group. In results not shown, heterogeneity was measured within each age-of-retirement category by separating a relative measure of education into four dummy variables representing the 0–25th, 26th–50th, 51st–75th, and 76th–100th percentiles in the education distribution. Regression estimates were quite similar to regression estimates for ages of retirement subdivided by earnings variables. An exception was that men retiring at AGE65 in the bottom quarter of the education distribution had higher mortality risk than men retiring at AGE65 in the top three-quarters of the education distribution.
| Variable | N b | Parameter estimate |
Odds ratio (confidence interval) |
|---|---|---|---|
| Intercept | 10.117 (7.3613) |
n.a. | |
| AGE62A, earn1 c | 1,064 | 0.4215 (0.0679)* |
1.52 (1.33–1.74) |
| AGE62A, earn2 c | 833 | 0.2053 (0.0768)* |
1.23 (1.06–1.43) |
| AGE62A, earn3 c | 822 | 0.3092 (0.0779)* |
1.36 (1.17–1.59) |
| AGE62A, earn4 c | 775 | 0.2357 (0.0783)* |
1.27 (1.09–1.48) |
| AGE62B to AGE63, earn1 c | 478 | 0.1650 (0.0864)** |
1.18 (1.00–1.40) |
| AGE62B to AGE63, earn2–earn3 c | 983 | 0.2141 (0.0688)* |
1.24 (1.08–1.42) |
| AGE62B to AGE63, earn4 c | 460 | 0.1280 (0.0898) |
1.14 (0.95–1.36) |
| AGE64, earn1 c | 449 | 0.2675 (0.0874)* |
1.31 (1.10–1.55) |
| AGE64, earn2–earn3 c | 1,034 | 0.1095 (0.0674) |
1.12 (0.98–1.27) |
| AGE64, earn4 c | 405 | -0.0952 (0.0988) |
0.91 (0.75–1.10) |
| AGE65, earn1 c | 281 | -0.00202 (0.1094) |
1.00 (0.81–1.24) |
| Black d | n.a. | 0.1728 (0.073)* |
1.19 (1.03–1.37) |
| Edu1 e | n.a. | 0.2996 (0.0616)* |
1.35 (1.20–1.52) |
| Edu2 e | n.a. | 0.1402 (0.0611)* |
1.15 (1.02–1.30) |
| Age | n.a. | 0.1048 (0.00348)* |
1.11 (1.10–1.12) |
| Year of birth | n.a. | -0.011 (0.00378)* |
0.99 (0.98–1.00) |
| Married in 1973 f | n.a. | -0.2554 (0.0535)* |
0.78 (0.70–0.86) |
| -2Log likelihood | 28053.892 | ||
| SOURCE: Author's calculations using the 1973 Exact Match. | |||
| NOTES: * = standard error significant at the 5 percent level. ** = standard error significant at the 10 percent level. n.a. = not applicable. Modeling the interaction of an education index and year of birth has a negligible effect on the other parameter estimates (results not shown). | |||
| a. Logistic regression results. | |||
| b. Sample counts are for the number of men in the sample before they are pooled in the regression. | |||
| c. Reference variable is AGE65 with earnings greater than the 25th percentile of the earnings distribution (earn2–earn4). | |||
| d. Reference variable = 1, if not black. | |||
| e. Reference variable (edu3) = 1, if 16 or more years of school. | |||
| f. Reference variable = 1, if not married in 1973. | |||
Life expectancy at age 65, by retirement-age and earnings subgroups (for married, white, college educated men born in 1930)
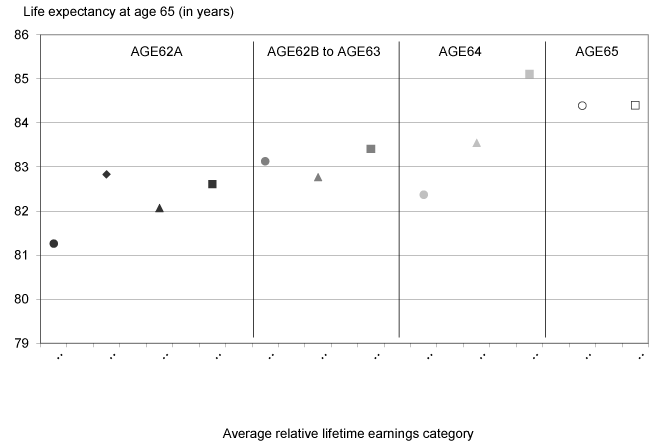
| Average relative lifetime earnings category |
Life expectancy |
|---|---|
| AGE62A | |
| Earn1 | 81.26 |
| Earn2 | 82.83 |
| Earn3 | 82.07 |
| Earn4 | 82.61 |
| AGE62B to AGE63 | |
| Earn1 | 83.13 |
| Earn2—earn3 | 82.77 |
| Earn 4 | 83.41 |
| AGE64 | |
| Earn1 | 82.37 |
| Earn2—earn3 | 83.55 |
| Earn4 | 85.11 |
| AGE65 | |
| Earn1 | 84.39 |
| Earn2—earn4 | 84.4 |
Recall that the nature of the heterogeneity among early retirees is crucial to the commonly held view of the world described by the health dichotomy school of thought—one in which a minority of men who retire early do so for poor health reasons and in which the majority of men who retire early are believed to be no different in health or longevity characteristics from men who retire at age 65. Empirical evidence suggests that this view of the world severely underestimates the extent to which early retirees differ from age 65 retirees. The data are more consistent with the idea that the majority of early retirees have higher mortality risk and a greater likelihood of being in poor health than age 65 retirees (even the majority of early retirees with earnings in the top quarter of the earnings distribution). The data also indicate that there is a small minority no different in health or longevity characteristics from men who retire at age 65 (men retiring at age 64 with earnings in the top quarter of the distribution or men retiring early with pension income in the top half or top quarter of the earnings distribution). Thus, the empirical evidence points to a combination of the benefits optimization view of the world and the health dichotomy view of the world—that is, a health trichotomy state of the world—with the size of the group of early retirees with life expectancy equal to age 65 retirees being quite small.
Appendix
This appendix discusses heterogeneity in the retirement-age reference variable. It then discusses the earnings imputations.
Heterogeneity in the Retirement-Age Reference Variable
It should be noted that Social Security's administrative rules may introduce a degree of heterogeneity into the AGE65 reference group. Before the 1977 Social Security amendments, beneficiaries were required to file for OASDI (Old-Age, Survivors, and Disability Insurance) and HI (Hospital Insurance) benefits simultaneously to be able to begin receiving HI benefits at age 65, even if they had no intention of also claiming OASDI benefits at age 65 (Myers 1993). For this analysis, retired-worker beneficiaries in birth cohorts 1908–1912 would be subject to that rule. After the 1977 amendments, beneficiaries were not required to file simultaneously, but such filing behavior was still allowed. The result could be a mixing of two distinct behavior groups into one reference group, with the relative sizes possibly changing over time. The concern is that beneficiaries who in actuality are receiving only HI benefits are disproportionately healthier than all other AGE65 retired-worker beneficiaries, and thus they would exaggerate differences between early retirees and age 65 retirees.20 (Under Social Security rules before 2000, if a beneficiary had earnings above an exempt amount from ages 65 to 69, the Social Security benefit was reduced by $1 for each $2 (before 1990) or by $1 for each $3 (starting in 1990) in excess of the annual exempt amount. Thus, if the beneficiary's earnings were high enough, the benefits were completely suspended.) Using the longitudinal earnings histories in the 1973 Exact Match, a proxy for those two groups of AGE65 retirees is created and then the mortality estimates are checked for sensitivity to heterogeneity in the reference group. Although the benefit-filing rules described earlier suggest that one should expect earlier birth cohorts to be more likely to have their benefits suspended than later birth cohorts, no such pattern is observed in the data.21 Thus, there is little danger of a year-of-birth effect clouding the results; however, one also cannot conclude such a pattern is nonexistent—as sample size by year of birth within each retirement age is rather small.
To create a dummy variable that identifies men who had their benefits suspended, the benefit reduction that individuals would face is calculated by observing their earnings over the earnings test amount at age 66 and subtracting that reduction from the average monthly benefit for the year in which they reached age 66.22 Earnings at age 66 rather than at age 65 are observed to allow for measurement imprecision.23 Men who are estimated to have had their benefits suspended are then deleted from the sample. About 41 percent of AGE65 retirees and 12 percent of AGE64 retirees are deleted. The other retirement-age categories have less than 5 percent of their members deleted. Rerunning the regressions estimated previously indicates no substantial change in any of the coefficients with this change in sample.24 To the extent that there is a slight change in the retirement-age coefficients, the majority of the parameter estimates increase slightly. This is the opposite direction of what we would expect if HI-only beneficiaries in the AGE65 retirement category are selectively healthier. If anything, it appears that the men with benefits suspended at age 66 who are entitled at the early retirement ages are slightly lowering adverse mortality risks before AGE65. AGE64 retirees experience the greatest change in mortality risk, with an increase of 5 percentage points in the odds of dying relative to AGE65 retirees. Of course, standard errors also increase, because of the decrease in sample size.
Earnings Imputations
Because the analyses conducted in this paper rely on earnings imputed above the Social Security taxable maximum (the level of earnings at which one no longer pays Social Security tax), there is legitimate concern over the sensitivity of results to imputation method. To check sensitivity, two imputation methods were compared—one that relies on the empirical distribution of an uncensored data set (results reported in the mortality section of this paper are based on this method) and a tobit that relies on a normality assumption (an assumption that is, in fact, violated by the data). Regression results do not change substantially when the tobit method is employed, leading to the conclusion that the analyses are not sensitive to imputation method.
The data used in this analysis contain men born from 1908 through 1931, so their earnings from ages 45 through 55 are observed from 1953 through 1986. Over this period, the Social Security taxable maximum rose from 115 percent of the real average wage in 1953 to 246 percent of the real average wage in 1986. Appendix Chart 1 shows the real taxable maximum and real average wage from 1953 through 1986. Because earnings data in the 1973 Exact Match are only observable up to the Social Security taxable maximum each year, censoring of earnings data by year follows the uneven path of the taxable maximum displayed in the chart.
Social Security real taxable maximum and real national average wage series, by year
| Year | Real Social Security taxable maximum |
Real national average wage index |
|---|---|---|
| 1953 | 16.8533 | 21.3608 |
| 1954 | 16.9159 | 21.28175 |
| 1955 | 16.8638 | 24.90542 |
| 1956 | 17.1141 | 24.54117 |
| 1957 | 17.6929 | 23.73834 |
| 1958 | 18.1726 | 23.11172 |
| 1959 | 18.3291 | 26.18787 |
| 1960 | 18.6159 | 25.78441 |
| 1961 | 18.8244 | 25.49882 |
| 1962 | 19.0382 | 25.21247 |
| 1963 | 19.2885 | 24.88529 |
| 1964 | 19.5336 | 24.57304 |
| 1965 | 19.8413 | 24.19196 |
| 1966 | 20.4357 | 32.29642 |
| 1967 | 20.9989 | 31.43022 |
| 1968 | 21.8801 | 35.64883 |
| 1969 | 23.0795 | 33.79623 |
| 1970 | 24.4196 | 31.94152 |
| 1971 | 25.4782 | 30.61441 |
| 1972 | 26.3177 | 34.19752 |
| 1973 | 27.9551 | 38.63338 |
| 1974 | 31.0316 | 42.53728 |
| 1975 | 33.8736 | 41.62534 |
| 1976 | 35.8081 | 42.72776 |
| 1977 | 38.1338 | 43.2687 |
| 1978 | 41.0331 | 43.13591 |
| 1979 | 45.721 | 50.08639 |
| 1980 | 51.8897 | 49.91357 |
| 1981 | 57.2086 | 51.91527 |
| 1982 | 60.6345 | 53.43493 |
| 1983 | 62.4752 | 57.14267 |
| 1984 | 64.6132 | 58.50198 |
| 1985 | 66.9024 | 59.1907 |
| 1986 | 67.94 | 61.81925 |
| 1987 | 70.3857 | -- |
| 1988 | 73.1807 | -- |
| 1989 | 76.7057 | -- |
| 1990 | 80.7469 | -- |
| 1991 | 84.006 | -- |
| 1992 | 86.4516 | -- |
| 1993 | 88.892 | -- |
| 1994 | 91.1343 | -- |
| 1995 | 93.7102 | -- |
| 1996 | 96.4531 | -- |
| 1997 | 98.62 | -- |
| 1998 | 100 | -- |
| NOTE: -- = not available. | ||
Because of the low taxable maximum over much of the working life of the men in the data, only 26.5 percent of the men in the sample have no earnings censored from ages 45 through 55. Until birth cohort 1923, about 50 percent or more of each birth cohort has from 6 to 11 years of earnings imputed from ages 45 through 55 (Appendix Table 1). Evidence of extensive censoring can also be seen in Appendix Table 2, where at least 81 percent of men in the 26th–50th earnings percentile (earn2) had at least 1 year of earnings imputed. Both the greater censoring for older birth cohorts (Appendix Table 1) and the fact that AGE65 retirees tend to have higher earnings than early retirees explain why more AGE65 retirees have from 6 to 11 years of earnings imputed than other retirees (Appendix Table 2). (Recall that the trend toward early retirement over time means that older cohorts have more AGE65 retirees than younger cohorts). Thus, it is prudent to check regression estimates for sensitivity to imputation method.
| Year of birth | Years imputed | ||
|---|---|---|---|
| 0 | 1 to 5 | 6 to 11 | |
| 1908 | 28.3 | 20.6 | 51.1 |
| 1909 | 30.6 | 21.3 | 48.1 |
| 1910 | 26.4 | 19.2 | 54.4 |
| 1911 | 23.1 | 22.5 | 54.5 |
| 1912 | 22.7 | 19.2 | 58.0 |
| 1913 | 25.6 | 19.7 | 54.7 |
| 1914 | 22.5 | 14.9 | 62.6 |
| 1915 | 17.7 | 18.9 | 63.5 |
| 1916 | 20.5 | 19.9 | 59.6 |
| 1917 | 21.6 | 18.2 | 60.2 |
| 1918 | 17.6 | 27.3 | 55.1 |
| 1919 | 21.0 | 23.9 | 55.1 |
| 1920 | 20.4 | 24.6 | 55.0 |
| 1921 | 25.1 | 22.3 | 52.6 |
| 1922 | 23.4 | 25.6 | 51.0 |
| 1923 | 27.0 | 29.3 | 43.7 |
| 1924 | 23.5 | 30.9 | 45.7 |
| 1925 | 24.8 | 30.6 | 44.6 |
| 1926 | 23.7 | 36.5 | 39.8 |
| 1927 | 34.4 | 27.9 | 37.7 |
| 1928 | 29.4 | 31.5 | 39.2 |
| 1929 | 35.5 | 33.0 | 31.5 |
| 1930 | 41.8 | 32.3 | 25.9 |
| 1931 | 46.3 | 25.3 | 28.4 |
| SOURCE: Author's calculations using the 1973 Exact Match. | |||
| Characteristic | Years imputed | ||
|---|---|---|---|
| 0 | 1 to 5 | 6 to 11 | |
| Full sample | 26.5 | 25.0 | 48.5 |
| Earn1 | 85.5 | 14.5 | 0 |
| Earn2 | 18.8 | 61.3 | 20.0 |
| Earn3 | 1.3 | 20.7 | 78.0 |
| Earn4 | 0 | 3.6 | 96.4 |
| Edu1 | 37.3 | 21.9 | 13.0 |
| Edu2 | 26.9 | 25.6 | 18.7 |
| Edu3 | 35.9 | 52.5 | 68.3 |
| AGE62A | 31.4 | 26.0 | 42.6 |
| AGE62B | 25.9 | 28.1 | 46.0 |
| AGE63 | 27.3 | 23.9 | 48.8 |
| AGE64 | 26.1 | 26.1 | 47.9 |
| AGE65 | 17.0 | 20.8 | 62.2 |
| SOURCE: Author's calculations using the 1973 Exact Match. | |||
Exploratory analysis of the data indicated that the earnings were not distributed normally, so a tobit regression—which requires a normality assumption—was not initially used for imputation. Instead, an empirical imputation method was employed.25 This method consists of first performing ordinary least squares (OLS) regressions on uncensored male earnings data from 1982 through 1999. The uncensored earnings data come from the 1992/1993 SIPP matched to Social Security detailed earnings records.26 The parameter estimates from these regressions are used to supply predicted values for the imputations, and the residuals are used to supply the error terms. Specifically, two separate equations are estimated. One equation regresses log-earnings on dummy variables representing ages 30–55 and period dummies representing years 1982–1983.
The other equation regresses log-earnings on dummy variables representing ages 30–55 and period dummies representing years 1982–1999. Predicted values and residuals from the first equation are used to impute earnings for censored values in the years 1951–1983 in the 1973 Exact Match. Estimates from the second equation are used to impute earnings for censored values in the years 1984–1996 in the 1973 Exact Match. It should be noted that imputations are performed on the 1973 Exact Match before the sample is restricted to retired-worker beneficiaries. Therefore, both samples should represent a random sample of the population; but because of the gap in time between the surveys, there may be some selective differences because of death or immigration. Both samples are restricted to men because of differences in earnings patterns of men and women.
Obviously, using data from 1982 through 1983 to represent earnings from 1951 through 1983 is not ideal, and would not be done if historical uncensored earnings data were readily available. The technique forces the assumption that the variance of earnings has been steady over the entire study period. Empirical evidence (covering the 1967–1999 period) indicates increased dispersion throughout the wage distribution from the mid-1970s to mid-1980s (Deere 2001). Dispersion then slowed, except for the 90th percentile, for which dispersion continued to grow (Deere 2001). Unfortunately, because the uncensored data begins in 1982, one is forced to use data with perhaps greater variation than the years for which one is imputing. Although data before 1967 are much more limited, Goldin and Katz (2001) find a gradual increase in the 90–10 log-wage differential in the 1950s through the 1960s and a steeper increase in the 1980s. In conclusion, the error may not be as bad as it could be—that is, at least there was some dispersion in the earlier years of the data, although probably not as much as in the 1982–1983 period.
To check the sensitivity of results to imputation, a right-censored tobit regression was conducted on the earnings data in the 1973 Exact Match. The tobit is performed on the same sample used in the subsequent regression analyses. Imputations for the censored earnings are estimated randomly around the predicted log-earnings and the standard deviation estimated in the tobit. As indicated in Appendix Table 3, the levels of average relative earnings (relative to the real national average wage) from ages 45 through 55 by percentile differ by type of imputation. The tobit method appears to impute a higher level than the rough empirical method.
| Earnings percentile |
Rough empirical method |
Tobit-random draws around means |
|---|---|---|
| 95 | 2.279 | 9.233 |
| 75 | 1.828 | 5.345 |
| 50 | 1.540 | 3.278 |
| 25 | 0.955 | 1.062 |
| SOURCE: Author's calculations using the 1973 Exact Match. | ||
However, this difference in level does not translate into substantive differences in regression outcomes (results not shown—in general, parameter estimates change very slightly). Recall that earnings from ages 45 through 55 for each individual are measured relative to the national average wage that corresponds to the year the earnings are recorded in the administrative earnings records. The relative earnings are then averaged over the number of years each individual had nonzero earnings from ages 45 through 55. To avoid unintended interactions between year of birth and earnings level, an individual's position in the earnings distribution (used to construct the four dummy earnings variables) is based on the earnings distribution for that individual's year of birth. Average relative earnings are then grouped into four categories for estimation that correspond to the following four positions in the earnings distribution: 0–25th percentile (earn1), 26th–50th percentile (earn2), 51st–75th percentile (earn3), and 76th–100th percentile (earn4). The robustness of the regression results implies that by making the earnings variables rely on relative position in the earnings distribution, potential errors in the level of earnings imputed probably do not affect results.
Notes
1 Under a full retirement age of 65 (which applies to all men in this sample), the actuarial reduction factor applied to an exactly age 62 benefit was 80 percent of the full age 65 benefit and was increased for each month of claim past age 62 until full benefits were reached at age 65. The 80 percent benefit factor was first adopted in 1965 and was based on life tables for women available at the time (Duggan and Soares 2001).
2 To simplify discussion, retirees who claim benefits after the full retirement age—a small group—are not considered.
3 Social Security retired worker is a term used to describe a person who receives Social Security benefits based on his or her own earnings record and does not include a Social Security disabled worker.
4 For all the birth cohorts in this study (the youngest cohort was born in 1931), the full retirement age was 65. Starting with the 1938 birth cohort, the full retirement age increases to age 65 and 2 months, eventually reaching age 67 for cohorts born in 1960 or later. The full retirement age is the age at which an individual can first retire and receive his or her full benefit without any reductions for early retirement.
5 The full 2001 SIPP (including topical modules) was not available at the time of this research. The 1996 panel was available, but nothing is gained by moving to the 1996 survey because the sample must still be restricted to men surviving to age 66 (which restricts the sample to older birth cohorts). For this analysis, the use of the 1992/1993 survey rather than the 1996 survey is expected to have no impact on the results. The SIPP is a multistage-stratified sample of the civilian noninstitutionalized population of the United States.
6 Because insured men who die before claiming benefits are not observed as retired-worker beneficiaries, one does not know at what age these men died. If those unobserved men died at age 66 or older without claiming benefits, they might more appropriately be placed in the reference variable and would lower the health of the reference variable if they were observed. Thus, if one does not require that all men survive to the same age, the men who are observed retiring at ages older than 65 are selectively healthier than the men not observed, and the reference variable might be biased towards better health. Analytically, it is more appealing to restrict the reference variable to AGE65 retirees so as to minimize the possibility of heterogeneity in the reference variable. Theoretically, one could expect men retiring after the full retirement age to be healthier and longer-lived than those retiring at AGE65 and thus could exaggerate the contrast between early and other retirees. (Practically, it really does not affect the estimates because there are so few men retiring at age 66 or older. Only 138 men are dropped from the sample because of this restriction.)
7 There may be some men in the earn1 category who have low observable covered earnings and higher unobservable non–Social Security–covered earnings. Those men would be misclassified as low earners in the data. It is unclear how many men are in that group, but their presence would push the effect of low earnings on poor health and mortality downward. Thus, coefficients on earn1 variables could be underestimated.
8 Although a tobit regression requires a normality assumption and the earnings are not normal, results are unlikely to be affected by use of the tobit because the earnings are measured in relative terms (see appendix).
9 The index is constructed using relative proportions observed in the 1973 CPS (Exact Match) for the same birth cohorts, because the 1973 Exact Match sample is larger.
10 Although Social Security's benefit formula is weighted so that a higher percentage of low-wage earners' preretirement earnings is replaced compared with that of high-wage workers, this is not expected to affect the correlation between poor health and earnings.
11 This statistic is calculated by taking the difference in the parameter estimates in Table 6 between AGE62A, earn1 and AGE62A, earn4 and dividing by the parameter estimate at AGE62A, earn1.
12 Specifically, the birth cohort subgroups are 1906–1911, 1912–1917, 1918–1923, and 1924–1930.
13 Wolfson and others (1993, S175) found higher earnings associated with later retirement and a "generally positive association between survival probability and age of retirement."
14 Deaths in the 1973 Exact Match are observed on the MBR, Numident, and Master Earnings File. A total of 346 men are deleted from the sample because they died between ages 62 and 65.
15 Waldron (2002) includes a test of the robustness of the discrete-time logistic regression model. Parameters were re-estimated using a complementary log-log model of continuous time. That type of model assumes an underlying Cox proportional hazards model and its coefficients have a relative risk interpretation (Allison 1995, 216–217). Parameter estimates and standard errors were affected only slightly by the alternative model, so this paper employs the computationally easier discrete-time logistic model.
16 Marital status is used in the 1973 Exact Match to provide consistency with previous work on the topic. In the 1992/1993 SIPP, the age at which the birth cohorts studied were asked their marital status was roughly 20 years older than in the 1973 Exact Match. Out of concern for the difficulty of cross data-set comparison on this variable and the proper interpretation of the variable when the response is given at older ages, it was not used in the analysis of the 1992/1993 SIPP.
17 Estimates of survival functions are constructed from the 1973 Exact Match data, using single-year age intervals and represent the probability that the individual deaths observed in the sample occur at age 80 or older. Censoring is taken into account. See Allison (1995) for details.
18 Although one cannot compare magnitude between the coefficients predicting the log-odds of lower self-reported health and the log-odds of death (as the dependent variables are measuring different results on different scales), it appears that the correlation between race and poorer health is stronger than the correlation between race and mortality. It would probably be unwise to read too much into this result, because it is unknown how much the mortality estimate is influenced by inaccurate death reporting for blacks. For example, Elo and Preston (1994, 427) conclude that "conventionally constructed African-American death rates may be seriously flawed as early as age 50."
19 Also recall that this example only includes men, ignoring the difference in life expectancy by gender. Nongender neutral improvements in longevity could also create a nonneutral distributional impact.
20 For example, Packard (1985) finds that Medicare-only beneficiaries are the least likely to report work-limiting health conditions, compared with beneficiaries receiving benefits at ages 62, 63–64, 65, and 66 or older.
21 Earlier birth cohorts are more likely to have later ages of retirement, but recall that no interaction between year of birth and retirement age has been found.
22 The $1 reduction for each $2 in earnings reduction rule is used for all years even though the reduction changes to $1 for $3 in 1990, to avoid inducing bias by deleting different cohorts at different rates. Average monthly benefit amounts for men are taken from the Annual Statistical Supplement, 2001 to the Social Security Bulletin, Table 5.B4, p. 198. Recomputation of benefits and of the reduction due to earnings over the earnings test amount is not attempted.
23 Although age is available in months, earnings are only reported annually, so that men with earnings at age 64 could be mistakenly thought to have earnings at age 65.
24 To prevent sample selection effects, the sample is also restricted to members of birth cohorts 1908–1929 who lived to at least age 67. The sample is reduced by 987 observations from those restrictions and by 930 observations from the deletion of men with earnings suspended at age 66.
25 The rough empirical method was generously estimated for the author by David Pattison of the Social Security Administration, Office of Research, Evaluation, and Statistics; the author estimated the tobit regressions.
26 Detailed (uncensored) earnings are only available from years 1978 to 1999. Years 1978 to 1981 are not used because of data quality problems.
References
Allison, Paul D. 1995. Survival Analysis Using the SAS System: A Practical Guide. Cary, NC: SAS Institute.
Bazzoli, Gloria J. 1985. "The Early Retirement Decision: New Empirical Evidence on the Influence of Health." Journal of Human Resources 20(2):214–234.
Burkhauser, Richard V.; Kenneth A. Couch; and John W. Phillips. 1996. "Who Takes Early Social Security Benefits? The Economic and Health Characteristics of Early Beneficiaries." The Gerontologist 36(6):789–799.
Deere, Donald R. 2001. "Trends in Wage Inequality in the United States." The Causes and Consequences of Increasing Inequality, edited by Finis Welch. Chicago: University of Chicago Press, pp. 9–35.
Duggan, James E., and Christopher J. Soares. 2001. Actuarial Nonequivalence in Early and Delayed Social Security Benefit Claims. Research Paper No. 2001–02. Washington, DC: U.S. Department of the Treasury, Office of Economic Policy. November.
Duleep, Harriet Orcutt. 1986. "Measuring the Effect of Income on Adult Mortality Using the Longitudinal Administrative Record Data." Journal of Human Resources 21:238–251.
———. 1989. "Measuring Socioeconomic Mortality Differentials Over Time." Demography 26(2):345–351.
Elo, Irma., and Samuel H. Preston. 1994. "Estimating African-American Mortality from Inaccurate Data." Demography 31(3):427–458.
Goldin, Claudia, and Lawrence F. Katz. 2001. "Decreasing (and Then Increasing) Inequality in America: A Tale of Two Half-Centuries." In The Causes and Consequences of Increasing Inequality, edited by Finis Welch. Chicago: University of Chicago Press, pp. 37–82.
Idler, Ellen L., and Yael Benyamini. 1997. "Self-Rated Health and Mortality: A Review of Twenty-Seven Community Studies." Journal of Health and Social Behavior 38(4):21–37.
Myers, Robert J. 1993. Social Security. 4th ed. Philadelphia, PA: Pension Research Council and University of Pennsylvania Press, p. 546.
National Commission on Retirement Policy. 1999. The 21st Century Retirement Security Plan. Final Report of the National Commission on Retirement Policy. Washington, DC: Center for Strategic and International Studies. March.
Olson, Janice A. 1999. "Who is "62 Enough?" Identifying Respondents Eligible for Social Security Early Retirement Benefits in the Health and Retirement Study." Social Security Bulletin 62(3):51–56.
Packard, Michael. 1985. "Health Status of New Retired-Worker Beneficiaries: Findings from the New Beneficiary Survey." Social Security Bulletin 48(2):5–16.
President's Commission to Strengthen Social Security. 2001. Strengthening Social Security and Creating Personal Wealth for All Americans.Final Report of the President's Commission to Strengthen Social Security (Reform Model 3). December.
Preston, Samuel H., and Irma T. Elo. 1995. "Are Educational Differentials in Adult Mortality Increasing in the United States?" Journal of Aging and Health 7(4):476–496.
RAND (Panis, Constantijn; Michael Hurd; David Loughran; Julie Zissimopoulos; Steven Haider; and Patricia StClair). 2002. The Effects of Changing Social Security Administration's Early Entitlement Age and the Normal Retirement Age. PM (Project Memorandum)-1332-SSA. Santa Monica, CA: RAND. June.
Sammartino, Frank J. 1987. "The Effect of Health on Retirement." Social Security Bulletin 50(2):31–47.
Simonovits, Andras. 2001. "Employment, Leisure and Pension: Incentives With Limits." Central European University (CEU) Working Paper No. 3/2001. Budapest, Hungary: Hungarian Academy of Sciences, Institute of Economics, CEU, and Budapest University of Technology and Business. March 15.
Smith, Ralph. 1999. Raising the Earliest Eligibility Age for Social Security Benefits. Washington, DC: Congressional Budget Office.
Social Security Advisory Board. 1999. "Implications of Raising the Social Security Retirement Age." Forum sponsored by the Social Security Advisory Board, October 13, 1998. Washington, DC: Social Security Advisory Board. www.ssab.gov/Report8.html.
Social Security Administration. 1997. "Option II: Publicly-Held Individual Accounts." In Findings and Recommendations. Vol. 1 of the Report of the 1994–1996 Advisory Council on Social Security. Washington, DC: Social Security Administration. January.
———. 2001. Annual Statistical Supplement to the Social Security Bulletin. Washington, DC: Office of Policy; Office of Research, Evaluation, and Statistics.
Uccello, Cori E. 1998. "Factors Influencing Retirement: Their Implications for Raising the Retirement Age." No. 9810. Washington, DC: American Association of Retired Persons, Public Policy Institute. October.
Waldron, Hilary. 2001. "Links Between Early Retirement and Mortality." ORES Working Paper Series, No. 93. Social Security Administration; Office of Policy; Office of Research, Evaluation, and Statistics. August.
———. 2002. "Do Early Retirees Die Early? Evidence from Three Independent Data Sets." ORES Working Paper Series, No. 97. Social Security Administration; Office of Policy; Office of Research, Evaluation, and Statistics. July.
Wolfson, Michael; Geoff Rowe; Jane F. Gentleman; and Monica Tomiak. 1993. "Career Earnings and Death: A Longitudinal Analysis of Older Canadian Men." Journal of Gerontology 48(4):S167–S179.