[Top]
[Prev]
SOCIAL SECURITY
DISABILITY INSURANCE PROGRAM
WORKER EXPERIENCE
ACTUARIAL STUDY NO. 114
by Tim Zayatz, A.S.A.
V. Technical Appendix on Table Construction Methodology
A. Overview
Select-and-ultimate tables 7A-9B
present probabilities of decrement from the Social Security Disability Insurance (DI) beneficiary rolls.
Table construction is based on 100 percent data from the Social Security Administration Master Beneficiary Record (MBR).
[Click here for List of Tables] Over 6.6 million records of disabled worker beneficiaries were analyzed over a 5-year period--January 1, 1991 through December 31, 1995. The primary variables for the study include: the reason for decrement from the DI rolls, and duration since entitlement. Concomitant variables include the age at entitlement to benefits, and gender of the beneficiary. The analysis reflects a total of roughly 13.6 million life-years of exposure for males and 8.1 million life-years of exposure for females. A 10-year select period was chosen for this study, implying that decrement for participants 10 or more years beyond selection is a function of attained age only.
The reasons for termination of DI benefits can be categorized as follows:
Decrement due to "all other reasons" is treated as withdrawal from the study, and directly affects exposure. However, separate decrement tables were not developed for this category. The table below provides a breakdown of the termination data collected from the MBR. Note that there exist differences in classifying various disability actions among the various data sources consulted for this study. As a result, termination counts stated here may differ from those stated elsewhere.
|
DI Disabled Worker Terminations by Reason
(January 1991-December 1995)
|
|
|
|
Male
|
|
Female
|
|
Total
|
|
Death
|
|
565,887
|
|
235,159
|
|
801,046
|
|
Recovery
|
|
83,637
|
|
44,382
|
|
128,019
|
|
Other
|
|
590,726
|
|
326,292
|
|
917,018
|
|
Total
|
|
1,240,250
|
|
605,833
|
|
1,846,083
|
|
|
|
|
|
|
|
|
|
Source: MBR database as of January 1998.
As stated in the study, various exogenous variables have an impact on disability recovery rates without actually affecting the underlying rate of medical improvement. These include the level of continuing disability review activity, budget restrictions, and legislation. To some extent, the same may be true for death rates. In any event, the prevailing administrative policy can have a large impact on the nature of allowances, and the degree of overall impairment- severity of the DI rolls. This results in fluctuating recovery and mortality rates over time. Ideally, the observation period would exhibit limited legislation and minimal effects from exogenous variables. However, it should be noted that the DI program experienced significant growth in claims during 1991-1995, which limited the number of reviews performed over that period.
B. Data Considerations
The mortality experience reported in this study is affected by several unique circumstances. First, it is recognized that a claimant may die while waiting for a disability determination. Since observation of a participant is contingent upon entitlement, a disability which results in death
prior
to entitlement will not be an "observed" death. As a result, the probability of death during the first year of entitlement may be artificially low.
Second, non-death and non-recovery terminations are almost exclusively comprised of beneficiaries who have either been automatically converted to old-age benefits upon attainment of normal retirement age (a disability action termed
conversion
), or have opted to receive old-age benefits in lieu of disability benefits
prior to
normal retirement age. In either case, observation stops with the last month in which DI benefits are paid. Since the decision to switch prior to full retirement age might be based on any number of unknown personal reasons (health, economic, etc.), it is not clear whether the mortality profile of the DI rolls changes significantly for attained ages 62 and older.
C. Data Collection
The model for this study utilizes a customized database that was constructed from 100 percent MBR data as of January 1998. The general record selection criteria are outlined below. The final data was subjected to numerous screenings and categorizations.
Included in the study are:
Excluded from the study are:
-
A primary claimant's entitled dependents (spouses and children);
-
Disability periods terminated or permanently suspended prior to January 1, 1991;
-
Beneficiaries dying or attaining age 65 prior to January 1, 1991
.
D. Underlying Methodology
The availability of complete data on each participant in the study (including date of birth, date of entitlement, and cause of decrement) allows us to directly estimate the
multiple-decrement probabilities
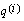 , where i
represents the cause of decrement. Alternatively, we could directly estimate the associated
single-decrement (absolute) rates
, where i
represents the cause of decrement. Alternatively, we could directly estimate the associated
single-decrement (absolute) rates
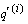 , which could then be used to derive the multiple-decrement probabilities. We chose the former method, making use of
scheduled exposure
of the observed population. Under this approach, the ordered pair
( r, s )
is determined for each age interval
, which could then be used to derive the multiple-decrement probabilities. We chose the former method, making use of
scheduled exposure
of the observed population. Under this approach, the ordered pair
( r, s )
is determined for each age interval
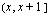 for which a participant is observed. The concept is that each participant enters the interval at age
for which a participant is observed. The concept is that each participant enters the interval at age
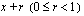 , and is scheduled to exit the interval at age
, and is scheduled to exit the interval at age
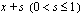 . Numerically,
s - r
is the amount of time (measured in life-years) that the participant is potentially under observation and exposed to the risk of decrement. Summing over all participants, we can calculate the scheduled exposure contributed to an interval.
. Numerically,
s - r
is the amount of time (measured in life-years) that the participant is potentially under observation and exposed to the risk of decrement. Summing over all participants, we can calculate the scheduled exposure contributed to an interval.
A participant may survive to the end of an interval, or may exit the study prior to the end of the interval in the event of:
-
Death;
-
Recovery or other non-death decrement;
-
Conversion to old-age benefits at age 65; or
-
The end of the observation period--termed an
observed ender
.
Based on this criteria, a
scheduled ending age
, x + s
, is established for an age interval in which the participant is expected to either survive to the end
( s = 1 )
, convert to old-age benefits prior to the end
( s < 1 )
, or become an observed ender
( s < 1 )
. Scheduled exposure is then credited to the appropriate interval (or
duration
since selection) using the following conditions: if the participant survives to the end of the interval, then exposure is credited from
x + r
to
x + 1; if the participant dies, converts to old-age benefits, or is an observed ender within the interval, then exposure is credited
from
x + r
to
x + s
; if the participant withdraws from the study during the interval (for example, recovers or switches to old-age benefits prior to age 65), then exposure is credited from
age
x + r
to
x + s
.
Note that in previous DI experience studies published by our office, the crediting of exposure for observed deaths was based on the
actuarial method
. Under this approach, exposure for a death is credited
from
x + r
to
x + 1
regardless of any scheduled ending age. For example,
assume
x + s
is a participant's expected age at the close of the observation period. If death occurs during the interval that closes the observation period, the actuarial method would credit exposure
up to age
x + 1
, which would be beyond the end of the observation period
whenever
s < 1
. We follow
Hoem's method
in this regard and credit exposure only
up to age
x + s
.
Multiple-decrement probabilities for an interval are found by dividing the observed number of deaths or recoveries by the aggregate scheduled exposure. Single-decrement rates are then derived from the probabilities using a constant force assumption for the distribution of decrement within a given interval. The method used in the construction of the select-and-ultimate multiple-decrement tables found in this study is detailed in chapter 9 of
Actuarial Mathematics
(Bowers et al. 1986).
For computation purposes, all dates are expressed as
decimal-dates
rounded to two decimal places (for example, 10-July-1993 is expressed as 1993.52). Coding detail is documented below for internal purposes. Variable acronyms are equivalent to those found in the description of the MBR database.
Entitlement dates
Various entitlement dates are converted to decimal-dates under the assumption that entitlement occurs on the first day of the month. Entitlement date variables include month and year of:
initial entitlement
(DOEI),
disability entitlement
(DOED), and
current entitlement
(DOEC).
Date of death
The decimal-date of death is calculated from the
beneficiary date of death
variable (BDOD), which states month, day, and year of death. Death on the 15th of the month is assumed for instances where the day of death is not recorded. Death on the 1st of the month is assumed for instances where the beneficiary dies in the month of the anniversary of entitlement. As an example, consider the following data for a participant who neither recovers nor switches to old-age benefits:
Date of entitlement: 1-July-1992
Date of death: 10-July-1993
Given death on 10-July-1993, the last month of entitlement to DI benefits is June-1993; hence the participant is only observed during the period July-1992 through June-1993. However, allowing that death occurs on 10-July-1993 is tantamount to allowing entry into the next observation interval--which would have begun at the entitlement anniversary on 1-July-1993--and Hoem's method would credit exposure from 1-July-1993 through the scheduled ending age for that interval. To avoid crediting exposure for the second interval (since the participant was not observed), the date of death is modified to be 1-July-1993, and exposure is credited only for the first interval. Also note that death is counted as having occurred exactly at the endpoint of the first interval, and is therefore included in that interval.
With respect to the MBR database, death carries a disability action code (termed
LAF code
) of "T1".
Date of conversion
With regard to conversion to old-age benefits, the last month of entitlement to DI worker benefits is the month before the month in which the worker attains
age 65 . For programming purposes, it is assumed that conversion takes place on the first day of the month of attainment of age 65; therefore, the calculated age at conversion is fractionally less than 65. Also note that if death occurs in the month of attainment of age 65, the case is counted as a conversion rather than an observed death.
Date of withdrawal
All other decrements occur on the first day of the month as coded in the
date of suspension or termination
(DOST), or
date of disability benefit cessation
(DDBC) variables. DOST provides detail on the date of suspension or termination of benefits for the most recent period of disability. Note that DOST corresponds to the value of the LAF code and is therefore subjected to continuous updating. As such, DOST will not provide a "history" of benefit termination for individuals with multiple periods of disability.
DDBC refers to the first month for which disability benefits are not payable. This variable is referenced for participants having multiple periods of disability, and for times when the DOST variable cannot provide an historical account of disability activity. The following examples illustrate the coding conventions used for the disability action variables DOST, DDBC, and LAF:
Example 1
DI benefits are payable for the month in which a beneficiary medically recovers, as well as the next 2 months. Consider a beneficiary having a single period of disability with recovery in April. The beneficiary remains entitled through June. At that time, LAF is coded as "T8" (indicating recovery) and DOST is coded as July.
Example 2
Consider a DI beneficiary who, though not medically recovered, begins to participate in SGA, with the following benefit payment history:
-
Benefits are paid throughout a 9-month trial work period during which SGA is performed--LAF code is "C" as DI benefits remain payable;
-
Following the trial work period, DI benefits are paid throughout the 36-month extended period of eligibility for those months in which SGA is not performed--LAF code is "C" for months in which DI benefits remain payable, and "S7" for months in which DI benefits are suspended;
-
Following the extended period of eligibility, DI benefits terminate, but Medicare benefits remain payable--LAF code is "U" when only Medicare benefits are payable;
-
Medicare benefits terminate--LAF code is "X7".
In this case DDBC is coded as the first month in which DI benefits are not payable; and DOST would vary with the different LAF codes, ultimately reflecting the date at which Medicare benefits terminate.
Select age
Since most beneficiaries do not become entitled to benefits on their exact birthdays, entitlement would normally occur at some fractional age. To facilitate exposure calculations, a participant's
insuring age
and corresponding
insuring date of birth
are substituted for the actual age at entitlement and actual date of birth. In this study, the insuring age is calculated to be the beneficiary's
age last birthday
as of entitlement. For example, consider the following beneficiary data:
Date of entitlement: 1-February-1992
Date of birth: 10-July-1960
Actual age at entitlement: 31 years, 206 days
Insuring age: 31 years
Insuring date of birth: 1-February-1961
Use of insuring age results in an integral
select age
at entitlement ensuring that subsequent durations begin on the entitlement anniversary. This is true whether the participant enters the study during the observation period, or is already part of the entitlement group when the observation period opens. However the
entry age
into the study for those already part of the entitlement group when the observation period opens may not be integral.
Entry age into the study
(YI)
For selection during the observation period, the entry age is the beneficiary's age as of the date of entitlement. For selection prior to the beginning of the observation period, the entry age is the beneficiary's age as of January 1, 1991. In either case, the beneficiary's age is measured from the insuring date of birth.
Scheduled exit age from the study
(ZI)
Participants are scheduled to exit the study either as an old-age conversion or an observed ender. If the participant will attain normal retirement age prior to the end of the observation period then
ZI
is the conversion age--as previously noted, this usually will be fractionally less than age 65. If the beneficiary will not attain age 65 prior to the end of the observation period, then
ZI
is the beneficiary's age as of December 31, 1995.
Actual exit age from the study due to death
(THI)
or withdrawal
(PSI)
If a participant dies within the observation period-- prior to conversion--then
THI
would reflect the date-of-death conventions mentioned earlier. If a participant withdraws from the study as a result of old-age conversion, then
PSI
would be the conversion age. If withdrawal occurs for any other reason, then
PSI
would be the age as of the withdrawal date. Both
THI
and
PSI
would be used in calculating exposure for absolute death and
withdrawal rates
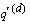 and
and
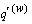 .
.
Duration
The intervals during which a participant is observed-- measured from the select age--are referred to as
durations
. For each select age
[x]
and duration
n
, we produce the ordered pair
( r , s )
representing each participant's scheduled exposure contribution to the
observation interval
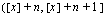 . For durations extending beyond the 10-year select period, exposure is credited to the appropriate attained age interval.
. For durations extending beyond the 10-year select period, exposure is credited to the appropriate attained age interval.
Fractional times
The fractional-time variables used to determine scheduled exposure contributions to an observation interval are defined below:
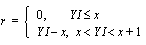
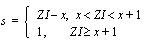
The amount of exposure contributed at each duration is summarized as follows:

Table construction
For each combination of select age and duration, the multiple-decrement
probabilities
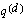 and
and
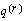 are calculated as the ratio of (a) the observed number of deaths or recoveries to (b) aggregate scheduled exposure. The probabilities are graduated and then used to obtain estimates for the absolute rates of
decrement
are calculated as the ratio of (a) the observed number of deaths or recoveries to (b) aggregate scheduled exposure. The probabilities are graduated and then used to obtain estimates for the absolute rates of
decrement
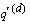 and
and
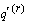 as outlined below (note that
d,
r, and
as outlined below (note that
d,
r, and
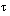 superscripts refer to death, recovery, and total decrement, respectively):
superscripts refer to death, recovery, and total decrement, respectively):
Estimate the total decrement probability:
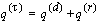
Under the assumption of constant force for each decrement over each age interval, derive estimates for the absolute rates:
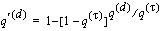
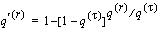
The graduated, multiple-decrement probabilities are shown in
tables 7A-9B; absolute rates appear in appendix tables
A.3A,
A.3B,
A.4A and
A.4B.
The life functions, expected future lifetimes, and life annuities presented in this study are based on the probabilities.
Probabilities versus absolute rates
The data for this study was collected in a multiple-decrement environment, however, we explicitly consider only two major decrements--death and recovery. The
quantity
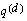 represents the probability of death in the presence of the other decrements. Mathematically, this is represented by:
represents the probability of death in the presence of the other decrements. Mathematically, this is represented by:
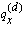 =
=
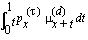
where
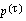 is the probability of neither dying nor recovering
prior to death at age
x + t; and
is the probability of neither dying nor recovering
prior to death at age
x + t; and
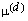 is the force of mortality.
is the force of mortality.
For each of the causes of decrement in a multiple-decrement model, it is possible to define a single-decrement model that depends only on a particular cause of decrement. The
quantity
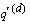 represents the absolute rate of death in the associated single-decrement environment. Mathematically, this is represented by:
represents the absolute rate of death in the associated single-decrement environment. Mathematically, this is represented by:
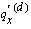 =
= 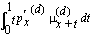
where
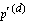 is the probability that
death
will not occur prior to age x + t.
is the probability that
death
will not occur prior to age x + t.
By defining a new fractional-time variable
k and withdrawal exposure (as shown below), absolute death rates could be calculated directly from the data as the ratio of deaths to aggregate exposure:


Graduation
The select-and-ultimate multiple-decrement probabilities were graduated using the two-dimensional Whittaker-Henderson
Type B method . The horizontal and vertical smoothing coefficients were chosen to obtain smoothness both across rows and down columns, while deviating as little as possible from the original estimates.
Life functions
Life tables
10A,
10B and
10C are constructed from the
blended select-and-ultimate probabilities shown in appendix tables
A.1A,
A.1B and
A.1C. The blended tables are
constructed from disability mortality
(Table 7A and
Table 7B) and
general population mortality for 1995. Results of the blending are
highlighted in the appendix tables. The two-step blending process involves the following:
-
Probabilities for
ultimate attained
ages 62 or older (duration "10+") are calculated by applying a constant mortality ratio to ultimate attained age 61. The mortality ratios are approximately 1.05 for males, and 1.06 for females. Under this assumption, disability mortality and the general population mortality for 1995 converge around age 90 for males, and age 94 for females.
-
Probabilities for
select attained ages
62 or older (durations 0-9) are blended into the ultimate probabilities derived in the first step by applying the duration-over-duration mortality ratios exhibited by select attained age 61. The resulting probabilities retain much of the characteristics of disability mortality in the earlier durations, then gradually reflect characteristics of general population mortality in the later durations.
The life functions
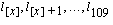 are first constructed for select age
[x] = 20, using a radix of 100,000. Life functions for
select ages
[x] > 20
are derived using the survival probabilities of the given select age.
For these ages,
are first constructed for select age
[x] = 20, using a radix of 100,000. Life functions for
select ages
[x] > 20
are derived using the survival probabilities of the given select age.
For these ages, 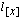 is calculated so that
is calculated so that 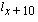 is attained. Note that
is attained. Note that 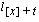 represents the number alive at the beginning of duration
t
from those originally entitled at [x].
represents the number alive at the beginning of duration
t
from those originally entitled at [x].
The blended death probabilities are added to the graduated recovery probabilities to produce the blended
total termination probabilities shown in
appendix tables
A.2A and
A.2B. These probabilities are used
to construct life tables
11A and
11B, respectively.
Expected future lifetime and annuity tables
Expectation tables 12A-14C and annuity tables 15A-18D
are produced from the life functions described above using basic actuarial principles found in any standard actuarial text on life contingencies.
[Click here for List of Tables]
E. Programs
For internal purposes, this section outlines the series of programs used to process data from the 100 percent MBR as of January 1998.
EXPCLASS--Program which classifies each record in the sample, and writes out the record (as it appears) along with the record's
classification code
. The main purpose is to distinguish which of the three most recent periods of disability ("DIB lines") contain relevant data with respect to the established observation period. A total of 14, 9, and 6 possible classifications were established for the first-most, second-most, and third-most recent periods of disability, respectively.
EXFORT--An original record may contain up to three periods of disability that must be split out, and an individual record written for each period. This program reconstructs the MBR record as it would have originally appeared at the time of disability. Depending on the individual classifications of the DIB lines, certain information is written to create up to three separate records from the original record.
EXT5MAIN--Program which processes the records written out by EXFORT and defines all variables needed to tabulate exposure, and classify deaths, recoveries, and all other terminations by select age, gender, and duration.
EXT5EXP--Program which calculates exposure in aggregate life-years based on output from EXT5MAIN.
EXT5DTH--Program which tabulates DI deaths based on output from EXT5MAIN.
EXT5RCV--Program which tabulates DI recoveries based on output from EXT5MAIN.
EXT5OTH--Program which tabulates DI terminations for "all other reasons" based on output from EXT5MAIN.
wh2dgrad.f--Program which performs the Whittaker-Henderson Type B two-dimensional graduation. Required input includes the ungraduated values, graduation weights, and the choice of horizontal and vertical smoothing coefficients.
[Top]
[Prev]
July 30, 1999
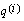 , where i
represents the cause of decrement. Alternatively, we could directly estimate the associated
single-decrement (absolute) rates
, where i
represents the cause of decrement. Alternatively, we could directly estimate the associated
single-decrement (absolute) rates
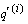 , which could then be used to derive the multiple-decrement probabilities. We chose the former method, making use of
scheduled exposure
of the observed population. Under this approach, the ordered pair
( r, s )
is determined for each age interval
, which could then be used to derive the multiple-decrement probabilities. We chose the former method, making use of
scheduled exposure
of the observed population. Under this approach, the ordered pair
( r, s )
is determined for each age interval
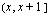 for which a participant is observed. The concept is that each participant enters the interval at age
for which a participant is observed. The concept is that each participant enters the interval at age
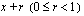 , and is scheduled to exit the interval at age
, and is scheduled to exit the interval at age
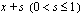 . Numerically,
s - r
is the amount of time (measured in life-years) that the participant is potentially under observation and exposed to the risk of decrement. Summing over all participants, we can calculate the scheduled exposure contributed to an interval.
2
. Numerically,
s - r
is the amount of time (measured in life-years) that the participant is potentially under observation and exposed to the risk of decrement. Summing over all participants, we can calculate the scheduled exposure contributed to an interval.
2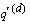 and
and
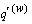 .
.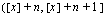 . For durations extending beyond the 10-year select period, exposure is credited to the appropriate attained age interval.
. For durations extending beyond the 10-year select period, exposure is credited to the appropriate attained age interval.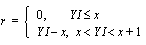
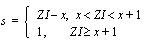

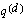 and
and
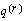 are calculated as the ratio of (a) the observed number of deaths or recoveries to (b) aggregate scheduled exposure. The probabilities are graduated and then used to obtain estimates for the absolute rates of
decrement
are calculated as the ratio of (a) the observed number of deaths or recoveries to (b) aggregate scheduled exposure. The probabilities are graduated and then used to obtain estimates for the absolute rates of
decrement
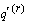 as outlined below (note that
d,
r, and
as outlined below (note that
d,
r, and
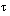 superscripts refer to death, recovery, and total decrement, respectively):
superscripts refer to death, recovery, and total decrement, respectively):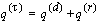
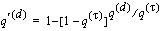
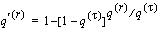
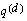 represents the probability of death in the presence of the other decrements. Mathematically, this is represented by:
represents the probability of death in the presence of the other decrements. Mathematically, this is represented by: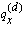 =
=
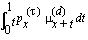
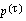 is the probability of neither dying nor recovering
prior to death at age
x + t; and
is the probability of neither dying nor recovering
prior to death at age
x + t; and
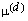 is the force of mortality.
is the force of mortality.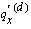 =
= 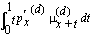
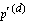 is the probability that
death
will not occur prior to age x + t.
is the probability that
death
will not occur prior to age x + t. 

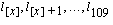 are first constructed for select age
[x] = 20, using a radix of 100,000. Life functions for
select ages
[x] > 20
are derived using the survival probabilities of the given select age.
For these ages,
are first constructed for select age
[x] = 20, using a radix of 100,000. Life functions for
select ages
[x] > 20
are derived using the survival probabilities of the given select age.
For these ages, 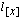 is calculated so that
is calculated so that 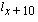 is attained. Note that
is attained. Note that 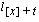 represents the number alive at the beginning of duration
t
from those originally entitled at [x].
represents the number alive at the beginning of duration
t
from those originally entitled at [x].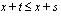 ; a participant observed to withdraw from the study during the interval does so at age
; a participant observed to withdraw from the study during the interval does so at age
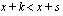 .
.