Actuarial Study No. 116

by : Felicitie C. Bell and Michael L. Miller

IV. Methods

A. Definitions of Life Table Functions

The following are definitions of the standard actuarial functions used in this study to develop mortality rates based on mid-year population and annual death data.

D_x = the number of deaths at age x last birthday in a population during a year

P_x = the number of persons who are age x last birthday in a population at midyear

_yM_x = the central death rate for the subset of a population that is between exact ages x and x+y

_yq_x = the probability that a person exact age x will die within y years

The following are the additional definitions of standard life table functions. The table represents a hypothetical cohort of 100,000 persons born at the same instant who experience the rate of mortality represented by ₁q_x, the probability that a person age x will die within one year, for each age x throughout their lives. The stationary population definitions, that are given in parenthesis, refer to the population size and age distribution that would result if the rates of mortality represented by ₁q_x were experienced each year, past and future, for persons between exact ages x and x+1, and if 100,000 births were to occur uniformly throughout each year.

l_x = the number of persons surviving to exact age x, (or the number of persons reaching exact age x during each year in the stationary population)

d_x = the number of deaths between exact ages x and x+1, (or the number of deaths at age last birthday x each year in the stationary population)

L_x = the number of person-years lived between exact ages x and x+1, (or the number of persons alive at age last birthday x at any time in the stationary population) We assume a uniform distribution of deaths for ages greater than 0.

T_x = the number of person-years lived after exact age x, (or the number of persons alive at age last birthday x or older at any time in the stationary population)

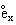= the average number of years of life remaining at exact age x

_ym_x = the central death rate for the population that is between exact ages x and x+y

_yf_x = separation factor; the average number of years not lived between exact ages x and x+y for those who die between exact ages x and x+y

The life table functions l_x, d_x, L_x, T_x, and 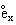were calculated as follows:

[D]

The fundamental step in constructing a life table from population data is that of developing probabilities of death, q_x, that accurately reflect the underlying pattern of mortality experienced by the population. The following sections describe the methods used for developing the rates presented in this actuarial study. These methods, as will be seen, vary significantly by age. Actual data permit the computation of central death rates, which are then converted into probabilities of death. Exceptions to this procedure include direct calculation of probabilities of death at young ages and geometric extrapolation of probabilities of death at extreme old age, where data is sparse or of questionable quality.

B. Death Rates at Ages 0 - 4

For the period 1940-1999, the probability of death at age 0 (q₀) was calculated directly from tabulations of births by month and from tabulations of deaths at ages 0, 1-2, 3-6, 7-28 days, 1 month, 2 months, ..., 11 months. For the period 1900-1939, that probability was calculated from the population central death rate at age 0 using the relationship between probabilities of death and central death rate determined by ordinary least squares regression on values for 1940-1999. After 1999, the probability was calculated from the population central death rate for age 0, assuming that the ratio of probability of death to central death rate measured for 1999 would remain constant thereafter.

For the period 1940-1999, probabilities of death at each age 1 through 4 (₁q_x,  x = 1, 2, 3, 4) were calculated from tabulations of births by year and from tabulations of deaths at ages 1, 2, 3, and 4 years. For the period 1900-1939, the probabilities were calculated from the population central death rate for the age group 1-4 using the relationship between probabilities of death and central death rate determined by ordinary least squares regression on values for 1940-1999. After 1999, the probabilities were calculated from the population central death rate for the age group 1-4 assuming that the ratio of probability of death to central death rate measured for 1999 would remain constant thereafter.

Based on a comparison of values from the 1900-1902 and 1909-1911 U.S. Decennial Life Tables, we concluded that the regression relationships used to determine probabilities of death from population central death rates during 1900-1939 gave reasonable results. The ratios used to determine probabilities of death from population central death rates after 1999 are assumed to give reasonable results because those probabilities are very low and are projected to change relatively little over the projection period. The following are the coefficients of the linear equation (y = mx+b) used for estimating probabilities of death as functions of population central death rates.

During the first year of life, mortality starts at an extremely high level, which becomes progressively lower, unlike mortality at other ages which does not change very much within a single year of age. Thus, it is particularly important at age 0 to estimate accurately the pattern of mortality throughout the year of age, as described above, for the calculation of ₁q₀.

Computation of other life table functions, particularly L_x, T_x, and 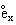requires an additional factor related to this pattern called the separation factor, which is the average fraction of a year not lived by those who die within the year. For each of the years 1940-1999 the separation factor at age 0 (₁f₀) was calculated directly from probabilities of death within the exact age intervals 0-1, 1-3, 3-7, and 7-28 days and 1-2, 2-3, ..., 11-12 months. For each of the years 1900-1939 that separation factor was linearly interpolated between the factor for 1940 and the factor calculated from the 1900-1902 U. S. Decennial Life Tables. Tests using data from the 1909-1911, 1919-1921, and 1929-1931 U. S. Decennial Life Tables showed that this interpolation gave reasonable results. For years after 1999, the separation factor at age 0 was assumed to remain constant at the 1999 level. Because mortality does not change very much within each of the second through fifth years of life, a separation factor of 1/2 was assumed.

C. Death Rates at Ages 5 - 94

One method that has been used to calculate probabilities of death for a life table that are consistent with the underlying pattern of mortality experienced in the population is to require that the life table central death rates for quinquennial age groups, ₅m_x, equal the population central death rates, ₅M_x. That is ₅m_x = ₅M_x for x = 5, 10, 15, ..., 90

[D]

Unfortunately, making these central death rates equal may introduce error when they should differ because the age distribution within the quinquennial age groups in the stationary population implied by the life table differs from that in the actual population under study. The degree of consistency can be improved using the relationship,

[D]

The central death rate for an age group is viewed in this equation as a weighted average of the central death rates for the single ages comprising the group. The degree of consistency between the level of mortality in the life table ₅m_x and the population ₅M_x is thus improved by eliminating the inconsistency in weighting by population at single year of age. This is accomplished by using the actual population as weights instead of the stationary population and producing 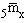. This means that,

[D]

Because 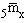has essentially the same implied age distribution as ₅M_x, a higher degree of consistency in the level of mortality is obtained by requiring 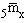= ₅M_x for x = 5, 10, 15, ..., 90. This requirement, which we use as the basis for constructing our life tables, is achieved by a rapidly-converging iterative process.

We assume that, initially, the separation factors for quinquennial age groups are such that deaths occurred on average at the midpoint of the age interval. That is ₅f_x = 2.5 for x = 5, 10, 15, ..., 90.

We proceed to calculate first approximations of probabilities of death within five years at exact quinquennial ages by the following relation:

[D]

Probabilities of death within one year are interpolated from the probability of death within five years based on the relationship ln (1-₅q_x) = ln (1-q_x) + ln (1-q_x+1) + ... + ln (1-q_x+4).

To accomplish the interpolation we apply a fourth degree osculatory formula developed by H.S. Beers to the natural logs of the complements of ₅q_x values, as suggested by the equation above.

For subsequent iterations, the separation factors were revised based on the ₅q_x of the previous iteration as follows:

[D]

The iteration process was continued until 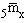was acceptably close to ₅M_x (within .00001) for x = 5, 10, 15, ..., 90.

D. Death Rates at Ages 95 and Older

It has been observed that the mortality rates of women, though lower than those of men, tend to increase faster with advancing age than those of men. An analysis of the mortality of Social Security charter Old-Age Insurance beneficiaries has shown that at the very old ages mortality increased about five percent per year of age for men and about six percent per year for women. Probabilities of death at each age 95 and older were calculated as follows for men:

[D]

For women, the same formulas were used, except that 1.06 was substituted for 1.05. The larger rate of growth in female mortality would eventually, at a very high age, cause female mortality to be higher than male mortality. At the point where this crossover would occur, we set female mortality equal to male mortality. The life table values for l_x, d_x, L_x, T_x and 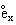were truncated at age 150. However, the life tables included in this study only show values through age 119.

E. Historical Trends and Projections

Any sound procedure for projecting mortality must begin with an analysis of past trends. In this actuarial study, the mortality experience in each year since 1900 has been summarized in age-adjusted central death rates in order to control for changes in the age distribution of the population. Rates were adjusted to the distribution of the 1990 U.S. resident census population. Final mortality data for both deaths and resident population, was available for years through 1999. Table 1 shows ageadjusted historical rates for 1900 through 1999.

An examination of the age-adjusted central death rates reveals several distinct periods of mortality reduction since 1900, as shown in Table 5. During the period 1900-1936, annual mortality reduction summarized for all ages, averaged about 0.8 percent for males and 0.9 percent for females. During the following period, 1936-1954, there was more rapid reduction, averaging 1.6 percent per year for males and 2.5 percent per year for females. The period 1954-1968 saw a much slower reduction of 0.8 percent per year for females and an actual increase of 0.2 percent per year for males. From 1968-1982 rapid reduction in mortality resumed, averaging 1.8 percent for males and 2.2 percent for females, annually. From 1982-1999, mortality rates decreased an average of 0.9 percent per year for males and 0.4 percent for females. More detailed analysis of average annual percent reduction in age-adjusted central death rates for selected periods is shown in Table 5.

For the entire period 1900 to 1999, mortality, summarized over all ages, declined at an average annual rate of 0.96 percent for males and 1.26 percent for females. However, mortality has generally declined at a slower rate for older individuals, throughout the last century. Between 1900 and 1999, the age-adjusted rates for ages 65 and older declined at an average annual rate of 0.59 for males and 0.88 percent for females.

For the period 1982-1999, the average annual rate of improvement for females was considerably less than that for males for all of the age groups shown in Table 5. For earlier historical periods, the opposite is true, i.e., the average annual rate of improvement for males was less than that for females.

A number of extremely important developments have contributed to the rapid average rate of mortality improvement during the twentieth century. These developments include:

Each of these developments is expected to make a substantially smaller contribution to annual rates of mortality improvement in the future.

Future reductions in mortality will depend upon such factors as:

Figure 1 shows historic and projected total male and female age-adjusted death rates per 100,000 population.

Figure 1
Age-Adjusted Central Death Rates by Sex and Calendar Year

[D]

Table 5 compares historical and projected average annual percentage reductions in age-adjusted central death rates during selected periods. Future reductions for those under age 65 are projected to be relatively small compared with past reductions. Reductions for the aged are expected to continue at a relatively rapid pace, as further advances are made against degenerative diseases, such as heart and vascular disease. For males age 65 and older, the average projected rate of improvement over the period 2026-2076 (0.71 percent per year) is slightly higher than that experienced over the last century (0.59 percent per year). The projected rate of improvement for women age 65 and older for the period 2026-2076 (0.69 percent per year) is slightly lower than that assumed for men (0.71 percent per year), and only about threefourths the rate experienced by aged women over the last century. This is consistent with the assumption that rates of mortality improvement for women, which had been faster than those for men until 1982, would ultimately be slightly less than those for males. Evidence that improvement for females will not always be faster than for males is apparent in data for years since 1981. The rate of improvement in mortality for aged women averaged only 0.22 percent per year during the period 1982-1999. This amount was less than one-third the average rate of improvement for aged men during this period (0.79 percent). Table 5 shows that, for all ages combined, the average rate of improvement under the intermediate alternative for the period 2026-2076 is 0.78 percent per year for men and 0.72 percent per year for women.

Given these assumed average annual rates of reduction, the actual projections of death rates are constructed on the basis of a consistent set of cause-specific ultimate rates of reduction. Toward this end, death rates for the years 1979-1999 were calculated and analyzed by age group and sex for the following seven groups of causes of death, based on the Tenth Revision of the International List of Diseases and Causes of Death code numbers:

Average annual percentage reductions in cause-specific death rates were calculated as the complement of the exponential of the slope of the least-squares line through the logarithms of the central death rates, multiplied by 100 to convert to percent form, and are given in Table 2. The sharpest reductions for the 1979 to 1999 period were in the categories of Heart Disease, averaging 2.1 percent and Vascular Disease, which averaged about 2.3 percent reduction per year. Violence averaged 1.1 percent reduction per year. On the other hand, Cancer, Respiratory Disease, Diabetes Mellitus and the residual group of Other Causes actually averaged an increase of about 0.2 to 2.0 percent per year.

Ultimate annual percentage reductions in central death rates by sex, age group, and cause of death were postulated for years after 2026. The broad age groups for which specific rates of reduction were selected are: under age 15, ages 15-49, ages 50-64, ages 65-84, and age 85 and older. The postulated ultimate annual percentage reductions are shown in Table 3.

Annual reductions in mortality by age, sex, and cause from 1999 to 2000 and from 2000 to 2001, were assumed to equal the average annual reductions observed for the period 1979-1999. For years after 2001, the reductions in mortality were assumed to change from initial levels of 100 percent of the average annual reductions observed for the period 1979-1999, to the postulated ultimate percentage reductions shown in Table 3, whenever these initial rates of reduction were positive. However, if the initial rates of reduction for a specific age, sex, and cause group was negative, the initial level was assumed to be 75 percent of the 1979-1999 average annual reduction. The postulated ultimate percentage reductions were assumed to apply after the year 2026. Tables 4a and 4b show historical and projected age-adjusted central death rates by cause of death and sex for the period 1979-2100.

Even though ultimate annual percentage reductions in central death rates are postulated for the seven causes listed in Table 3, the resulting percentage reduction in age-adjusted central death rates for all causes combined are carefully reviewed, analyzed, and adjusted to assure consistency with the overall assumed rates of reduction. For each age and sex group, the decomposition of the percentage reduction by causes also provides a useful tool to test the reasonableness of the overall reduction.

List of Studies