Life Tables for the
United States Social Security
Area 1900-2100





by Felicitie C. Bell
and Michael L. Miller
Life Tables for the |
 |
 |
 |
 |
 |
ACTUARIAL STUDY NO. 120
by Felicitie C. Bell and Michael L. Miller | |||||
I. Introduction
Each year, estimates of future income and expenditures of the Old-Age, Survivors, and Disability Insurance (OASDI) program are presented to the Congress in the Annual Report of the Board of Trustees. These estimates illustrate possible scenarios of the future financial position of the OASDI program, under present law, and thus are valuable in the policy making process for the program.
To produce these financial estimates, projections of the population in the Social Security coverage area are needed. One of the essential components of population projections is a projection of mortality, which is the subject of this study. For the 2005 Trustees Report, three separate projections—intermediate, low cost, high cost—were prepared. These projections are based on three different sets of assumptions about future death rates. The intermediate projections reflect the Trustees' best estimate of future experience. All mortality projections presented in this study are from the intermediate projections of the 2005 Annual Report of the OASDI Board of Trustees. These projections were also used in estimating the future financial status of the Hospital Insurance (HI) and Supplementary Medical Insurance (SMI) programs as described in the 2005 Annual Report of the Medicare Board of Trustees.
Mortality rates are presented in this study in the context of life tables, which are commonly used by actuaries and demographers. Tables on both period and cohort bases are included. These tables supersede those published in Actuarial Study Number 116, which were used in the preparation of the 2002 Annual Reports
II. Basic Concepts
A life table is a concise way of showing the probabilities of a member of a particular population living to or dying at a particular age. In this study, the life tables are used to examine the mortality changes in the Social Security population over time.
An ideal representation of human mortality would provide a measure of the rate of death occurring at specified ages over specified periods of time. In the past, analytical methods (such as the Gompertz, Makeham, or logistic curves) satisfied this criterion approximately over a broad range of ages. However, as actual data have become more abundant and more reliable, the use of approximate analytical methods have become less necessary and acceptable. Today, mortality is most commonly represented in the form of a life table, which gives probabilities of death within one year at each exact integral age. These probabilities are generally based on tabulations of deaths in a given population and estimates of the size of that population. For this study, functions in the life table can be generated from the qx, where qx is the probability of death within a year of a person aged x. Although a life table does not give mortality at non-integral ages or for non-integral durations, as can be obtained from a mathematical formula, acceptable methods for estimating such values are well known.
Two basic types of life tables are presented in this study, period-based tables and cohort-based tables. Each type of table can be constructed either based on actual population data or on expected future experience.
A period life table is based on, or represents, the mortality experience of an entire population during a relatively short period of time, usually one to three years. Life tables based directly on population data are generally constructed as period life tables because death and population data are most readily available on a time period basis. Such tables are useful in analyzing changes in the mortality experienced by a population through time. If the experience study is limited to short periods of time, the resulting rates will be more uniformly representative of the entire period. This study presents period life tables by sex for decennial years 1900 through 2000 based on United States and Medicare data, and for decennial years 2010 through 2100 reflecting projected mortality.
A cohort, or generation, life table is based on, or represents, mortality experience over the entire lifetime of a cohort of persons born during a relatively short period of time, usually one year. Cohort life tables based directly on population experience data are relatively rare, because of the need for data of consistent quality over a very long period of time. Cohort tables can, however, be readily produced, reflecting mortality rates from a series of period tables for past years, projections of future mortality, or a combination of the two. Such tables are superior to period tables for the purpose of projecting a population into the future when mortality is expected to change over time, and for analyzing the generational trends in mortality. This study presents cohort life tables by sex for births in decennial years 1900 through 2100, reflecting the mortality experience and projections described above.
A life table treats the mortality experience upon which it is based as though it represents the experience of a single birth cohort consisting of 100,000 births who experience, at each age x of their lives, the probability of death, denoted qx, shown in the table. The entry lx in the life table shows the number of survivors of that birth cohort at each succeeding exact integral age. Another entry, dx, shows the number of deaths that would occur between succeeding exact integral ages among members of the cohort. The entry denoted Lx gives the number of person-years lived between consecutive exact integral ages x and x+1 and Tx gives the total number of person-years lived beyond each exact integral age x, by all members of the cohort. The final entry in the life table, 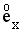 , represents the average number of years of life remaining for members of the cohort still alive at exact integral age x, and is called the life expectancy.
, represents the average number of years of life remaining for members of the cohort still alive at exact integral age x, and is called the life expectancy.
The lx entry in the life table is also useful for determining the age corresponding to a specified survival rate from birth, which is defined as the age at which the ratio of lx to 100,000 is equal to a specified value between 0 and 1.
A stationary population is what would result if for each past and future year:
A population with these characteristics would have a constant number of persons from year to year (in fact, at any time) both in their total number and in their number at each age. These numbers of persons, by age last birthday, are provided in the life table as the Lx values. The lx entry is interpreted as the number of persons who attain each exact integral age during any year, and dx is the number of persons who die at each age last birthday during any year. The entry Tx represents the number of persons who are alive at age last birthday x or older, at any time.
III. Construction of Central Death Rates
A. Data Sources
Annual tabulations of numbers of deaths by age and sex are made by the National Center for Health Statistics (NCHS) based on information supplied by States in the Death Registration Area, and are published in the volumes of Vital Statistics of the United States. These are now available on the web at www.cdc.gov/nchs/nvss.htm. Deaths are provided by five year age groups for ages 5 through 84, in total for ages 85 and older, and by single-year and smaller age intervals for ages 4 and under. One requirement for admission to the Death Registration Area, which since 1933 has included all the States, the District of Columbia and the independent registration area of New York City, was a demonstration of ninety percent completeness of registration. Because incentives for filing a death certificate are so strong (obtaining burial permits, collecting insurance benefits, settling estates, etc.) and because every State has adopted laws that require the registration of deaths, it is believed that errors of under-registration of deaths are insignificant for the nation as a whole. Errors of misstatement of age on the death certificate, however, may very well cause distortion in the distribution of numbers of deaths by age group.
Annual estimates of the U.S. resident population by single year of age and sex are made by the Census Bureau and are published in Current Population Reports Series P-25. The most recent population information is available and updated regularly on the Census Bureau web site at www.census.gov. These estimates are affected by both undercount and misclassification in the decennial census. These errors, which may either offset or compound, are usually considered together as net undercount. Postcensal estimates are made by the "inflation-deflation" method which inflates the last previous census-level population by net undercount, carries the inflated population forward according to the births and deaths tabulated in the Vital Statistics, adjusts the population by estimated net immigration, and then deflates by net undercount. Thus, the postcensal population estimates are affected by errors in the Vital Statistics and the effect tends to accumulate as the elapsed time from the last previous census increases. When results of the following census become available, the postcensal estimates are revised, and are then called intercensal estimates, thus removing much of the effect of errors in Vital Statistics and in net immigration estimates.
Central death rates calculated by comparing numbers of deaths tabulated by the National Center for Health Statistics to the mid-year population estimated by the Census Bureau are affected by the errors from both sources, which may either offset or combine. Further, errors of noncomparability of numerator and denominator may also be introduced. Although efforts are made to minimize errors of noncomparability (by excluding armed forces overseas from the population estimates, for example), complete comparability is intrinsically impossible.
The errors of noncomparability can be eliminated if the numbers of deaths and the population are drawn from the same source. This approach, however, generally involves so large a reduction in the size of the population being observed, that more random error is introduced than noncomparability error is eliminated. One source of data on aged persons which is not subject to errors of noncomparability and yet does permit a very large number of observations, is Medicare program enrollment. Also, this source involves fewer errors of misstatement of age, because most of the data relate to individuals who have had to prove their date of birth to become entitled to benefits.
An error analogous to net undercount does appear to be present in the Medicare data, although the error is believed to have an insignificant effect on calculated death rates, except for the very aged (beginning at roughly age 95). This error stems from the presence in the data of "phantom records" which may have arisen because the person was registered in the program more than once, or because information about a person was miscoded when he/she registered, or because the person's death was not reported. Such phantom records are not of much concern to cost-conscious program administrators, however, because the Medicare program only pays benefits when bills for covered services rendered are submitted.
In an effort to reduce the number of phantom records, the Medicare based death rates calculated for years after 1987 were limited to the records of those Medicare participants who were also eligible for Social Security or Railroad Retirement monthly income benefits, or who were government employees or retirees with enough Medicare qualifying government employment. This limitation eliminated approximately three percent of the Medicare records.
Data needed in order to project central death rates by cause of death were obtained from Vital Statistics tabulations for years since 1979. For the years 1979-1998, adjustments were made to the distribution of the numbers of deaths by cause. The adjustments were needed in order to reflect the revision in the cause of death coding that occurred in 1999, making the data for the years 1979-1998 more comparable with the coding used for the years 1999 and later. The adjustments were based on comparability ratios published by the National Center for Health Statistics.
For the years 1900-1967, age-sex specific central death rates were calculated from NCHS Vital Statistics tabulations of deaths and Census estimates of populations. For the period 1968-2001 those same two sources were used for ages under 65, but records of the Medicare program were used to calculate rates for ages 65 and over. The numbers of deaths by cause from Vital Statistics tabulations were used to distribute the age-sex specific rates into age-sex-cause specific rates for the years 1979-2001.
B. Adjustments in Population
Populations in some five-year age groups for some years were estimated from published figures for broader age groups. Death Registration States' populations during 1900-1932 for five-year age groups, 5-9 through 70-74, were estimated from the ten-year age groups, 5-14 through 65-74, by assuming that the distributions of five-year age groups within ten-year age groups were as published for the United States resident population from the Census Bureau. Death Registration States' populations during 1900-1932, and United States population during 1933-1939 for the age group 75-84, were distributed between the 75-79 and 80-84 age groups by using linear interpolation of the age distributions from the Decennial Census enumerations. Death Registration States' populations during years 1900-1932 and United States population during years 1933-1967 for age groups 85-89, 90-94, and 95 and over were estimated by distributing the age group 85 and over using NCHS tabulated deaths for each year and Medicare data. The split of the conterminous United States populations aged 0-4 into age groups 0 and 1-4 for the years 1950-1959 was estimated from the group 0-4 by assuming the same distribution as in the United States, Alaska, and Hawaii combined. For 1959, deaths occurring in Alaska were excluded from total deaths, so that the population of the conterminous United States could be used to calculate the death rates. For all years, deaths tabulated at "age unstated" were prorated across the tabulated age groups.
IV. Methods
A. Definitions of Life Table Functions
The following are definitions of the standard actuarial functions used in this study to develop mortality rates based on mid-year population and annual death data.
The following are the additional definitions of standard life table functions. The table represents a hypothetical cohort of 100,000 persons born at the same instant who experience the rate of mortality represented by 1qx, the probability that a person age x will die within one year, for each age x throughout their lives. The stationary population definitions, that are given in parentheses, refer to the population size and age distribution that would result if the rates of mortality represented by 1qx were experienced each year, past and future, for persons between exact ages x and x+1, and if 100,000 births were to occur uniformly throughout each year.
The life table functions lx, dx, Lx, Tx, and 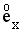 were calculated as follows:
were calculated as follows:
The fundamental step in constructing a life table from population data is that of developing probabilities of death, qx, that accurately reflect the underlying pattern of mortality experienced by the population. The following sections describe the methods used for developing the rates presented in this actuarial study. These methods, as will be seen, vary significantly by age. Actual data permit the computation of central death rates, which are then converted into probabilities of death. Exceptions to this procedure include direct calculation of probabilities of death at young ages and geometric extrapolation of probabilities of death at extreme old age, where data is sparse or of questionable quality.
B. Death Rates at Ages 0 - 4
For the period 1940-2001, the probability of death at age 0 (q0) was calculated directly from tabulations of births by month and from tabulations of deaths at ages 0, 1-2, 3-6, 7-28 days, 1 month, 2 months, ..., 11 months. For the period 1900-1939, that probability was calculated from the population central death rate at age 0 using the relationship between probabilities of death and central death rate determined by ordinary least squares regression on values for 1940-2001. After 2001, the probability was calculated from the population central death rate for age 0, assuming that the ratio of probability of death to central death rate measured for 2001 would remain constant thereafter.
For the period 1940-2001, probabilities of death at each age 1 through 4 (1qx, x=1,2,3,4) were calculated from tabulations of births by year and from tabulations of deaths at ages 1, 2, 3, and 4 years. For the period 1900-1939, the probabilities were calculated from the population central death rate for the age group 1-4 using the relationship between probabilities of death and central death rate. After 2001, the probabilities were similarly calculated from the population central death rate for the age group 1-4.
Based on a comparison of values from the 1900-1902 and 1909-1911 U.S. Decennial Life Tables, we concluded that the regression relationships used to determine probabilities of death from population central death rates during 1900-1939 gave reasonable results. The ratios used to determine probabilities of death from population central death rates after 2001 are assumed to give reasonable results because those probabilities are very low and are projected to change relatively little over the projection period. The following are the coefficients of the linear equation (y = mx+b) used for estimating probabilities of death as functions of population central death rates.
During the first year of life, mortality starts at an extremely high level, which becomes progressively lower, unlike mortality at other ages which does not change very much within a single year of age. Thus, it is particularly important at age 0 to estimate accurately the pattern of mortality throughout the year of age, as described above, for the calculation of 1q0. Computation of other life table functions, particularly Lx, Tx, and 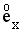 requires an additional factor related to this pattern called the separation factor, which is the average fraction of a year not lived by those who die within the year. For each of the years 1940-2001 the separation factor at age 0 (1f0) was calculated directly from probabilities of death within the exact age intervals 0-1, 1-3, 3-7, and 7-28 days and 1-2, 2-3, ..., 11-12 months. For each of the years 1900-1939 that separation factor was linearly interpolated between the factor for 1940 and the factor calculated from the 1900-1902 U.S. Decennial Life Tables. Tests using data from the 1909-1911, 1919-1921, and 1929-1931 U.S. Decennial Life Tables showed that this interpolation gave reasonable results. For years after 2001, the separation factor at age 0 was assumed to remain constant at the 2001 level. Because mortality does not change very much within each of the second through fifth years of life, a separation factor of ½ was assumed.
requires an additional factor related to this pattern called the separation factor, which is the average fraction of a year not lived by those who die within the year. For each of the years 1940-2001 the separation factor at age 0 (1f0) was calculated directly from probabilities of death within the exact age intervals 0-1, 1-3, 3-7, and 7-28 days and 1-2, 2-3, ..., 11-12 months. For each of the years 1900-1939 that separation factor was linearly interpolated between the factor for 1940 and the factor calculated from the 1900-1902 U.S. Decennial Life Tables. Tests using data from the 1909-1911, 1919-1921, and 1929-1931 U.S. Decennial Life Tables showed that this interpolation gave reasonable results. For years after 2001, the separation factor at age 0 was assumed to remain constant at the 2001 level. Because mortality does not change very much within each of the second through fifth years of life, a separation factor of ½ was assumed.
C. Death Rates at Ages 5 - 94
One method that has been used to calculate probabilities of death for a life table that are consistent with the underlying pattern of mortality experienced in the population is to require that the life table central death rates for quinquennial age groups, 5mx, equal the population central death rates, 5Mx. That is 5mx = 5Mx for x = 5, 10, 15, ..., 90
|
where
|
5mx
|
=
|
dx + dx+1 + dx+2 + dx+3 + dx+4
|
|
Lx + Lx+1 + Lx+2 + Lx+3 + Lx+4
|
|||
|
and
|
5Mx
|
=
|
Dx + Dx+1 + Dx+2 + Dx+3 + Dx+4
|
|
Px + Px+1 + Px+2 + Px+3 + Px+4
|
Unfortunately, making these central death rates equal may introduce error when they should differ because the age distribution within the quinquennial age groups in the stationary population implied by the life table differs from that in the actual population under study. The degree of consistency can be improved using the relationship,
The central death rate for an age group is viewed in this equation as a weighted average of the central death rates for the single ages comprising the group. The degree of consistency between the level of mortality in the life table 5mx and the population 5Mx is thus improved by eliminating the inconsistency in weighting by population at single year of age. This is accomplished by using the actual population as weights instead of the stationary population and producing 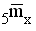 . This means that,
. This means that,
Because 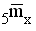 has essentially the same implied age distribution as 5Mx, a higher degree of consistency in the level of mortality is obtained by requiring
has essentially the same implied age distribution as 5Mx, a higher degree of consistency in the level of mortality is obtained by requiring 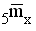 = 5Mx for x = 5, 10, 15, ..., 90. This requirement, which we use as the basis for constructing our life tables, is achieved by a rapidly-converging iterative process.
= 5Mx for x = 5, 10, 15, ..., 90. This requirement, which we use as the basis for constructing our life tables, is achieved by a rapidly-converging iterative process.
We assume that, initially, the separation factors for quinquennial age groups are such that deaths occurred on average at the midpoint of the age interval. That is 5fx = 2.5 for x = 5, 10, 15, ..., 90.
We proceed to calculate first approximations of probabilities of death within five years at exact quinquennial ages by the following relation:
Probabilities of death within one year are interpolated from the probability of death within five years based on the relationship ln (1-5 qx) = ln (1-qx)+ln (1-qx+1)+...+ln (1-qx+4).
To accomplish the interpolation we apply a fourth degree osculatory formula developed by H.S. Beers to the natural logs of the complements of 5qx values, as suggested by the equation above. Coefficients for starting and ending groups are as follows:
Coefficients for interior groups are as follows:
For subsequent iterations, the separation factors were revised based on the 5qx of the previous iteration as follows:
The iteration process was continued until 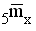 was acceptably close to 5Mx (within .00001) for x = 5, 10, 15, ..., 90.
was acceptably close to 5Mx (within .00001) for x = 5, 10, 15, ..., 90.
D. Death Rates at Ages 95 and Older
It has been observed that the mortality rates of women, though lower than those of men, tend to increase faster with advancing age than those of men. An analysis of the mortality of Social Security charter Old-Age Insurance beneficiaries has shown that at the very old ages mortality increased about five percent per year of age for men and about six percent per year for women. Probabilities of death at each age 95 and older were calculated as follows for men:
|
qx
|
= qx-1 · (
|
q94
|
·
|
99-x
|
+ 1.05 ·
|
x-94
|
)
|
x = 95, 96, 97, 98, 99
|
|
q93
|
5
|
5
|
||||||
|
qx
|
= 1.05 · qx-1
|
x = 100, 101, 102, ...
|
||||||
For women, the same formulas were used, except that 1.06 was substituted for 1.05. The larger rate of growth in female mortality would eventually, at a very high age, cause female mortality to be higher than male mortality. At the point where this crossover would occur, we set female mortality equal to male mortality. The life table values for lx, dx, Lx, Tx and 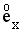 were truncated at age 150. However, the life tables included in this study only show values through age 119.
were truncated at age 150. However, the life tables included in this study only show values through age 119.
E. Historical Trends and Projections
Any sound procedure for projecting mortality must begin with an analysis of past trends. In this actuarial study, the mortality experience in each year since 1900 has been summarized in age-adjusted central death rates in order to control for changes in the age distribution of the population. Rates were adjusted to the distribution of the 2000 U.S. resident census population. Final mortality data for both deaths and resident population, were available for years through 2001. Table 1 shows age-adjusted historical rates for 1900 through 2001.
An examination of the age-adjusted central death rates reveals several distinct periods of mortality reduction since 1900, as shown in Table 5. During the period 1900-1936, annual mortality reduction summarized for all ages, averaged about 0.7 percent for males and 0.8 percent for females. During the following period, 1936-1954, there was more rapid reduction, averaging 1.6 percent per year for males and 2.4 percent per year for females. The period 1954-1968 saw a much slower reduction of 0.7 percent per year for females and an actual increase of 0.2 percent per year for males. From 1968-1982 rapid reduction in mortality resumed, averaging 1.8 percent for males and 2.2 percent for females, annually. From 1982-2001, mortality rates decreased an average of 1.0 percent per year for males and 0.4 percent for females. More detailed analysis of average annual percentage reduction in age-adjusted central death rates for selected periods is shown in 5.
For the entire period 1900 to 2001, mortality, summarized over all ages, declined at an average annual rate of 0.93 percent for males and 1.19 percent for females. However, mortality has generally declined at a slower rate for older individuals, throughout the last century. Between 1900 and 2001, the age-adjusted rates for ages 65 and older declined at an average annual rate of 0.59 percent for males and 0.84 percent for females.
For the period 1982-2001, the average annual rate of improvement for females was considerably less than that for males for most of the age groups shown in 5. For earlier historical periods, the opposite is true, i.e., the average annual rate of improvement for males was generally less than that for females.
A number of extremely important developments have contributed to the rapid average rate of mortality improvement during the twentieth century. These developments include:
Each of these developments is expected to make a substantially smaller contribution to annual rates of mortality improvement in the future.
Future reductions in mortality will depend upon such factors as:
Figure 1 shows historic and projected total male and female age-adjusted central death rates per 100,000 population.
Table 5 compares historical and projected average annual percentage reductions in age-adjusted central death rates during selected periods. Future reductions for those under age 65 are projected to be relatively small compared with past reductions. Reductions for the aged are expected to continue at a relatively rapid pace, as further advances are made against degenerative diseases, such as heart and vascular disease. For males age 65 and older, the average projected rate of improvement over the period 2029-2079 (0.68 percent per year) is slightly higher than that experienced over the last century (0.59 percent per year). The projected rate of improvement for women age 65 and older for the period 2029-2079 (0.66 percent per year) is slightly lower than that assumed for men (0.68 percent per year), and only about three-fourths the rate experienced by aged women over the last century (0.84 percent per year). This is consistent with the assumption that rates of mortality improvement for women, which had been faster than those for men until 1982, would ultimately be slightly less than those for males. Evidence that improvement for females will not always be faster than for males is apparent in data for years since 1981. The rate of improvement in mortality for aged women averaged only 0.15 percent per year during the period 1982-2001. This amount was about one-fifth the average rate of improvement for aged men during this period (0.77 percent). Table 5 shows that, for all ages combined, the average rate of improvement under the intermediate alternative for the period 2029-2079 is 0.72 percent per year for men and 0.68 percent per year for women.
Given these assumed average annual rates of reduction, the actual projections of death rates are constructed on the basis of a consistent set of cause-specific ultimate rates of reduction. Toward this end, death rates for the years 1981-2001 were calculated and analyzed by age group and sex for the following seven groups of causes of death, based on the Tenth Revision of the International List of Diseases and Causes of Death code numbers:
Average annual percentage reductions in cause-specific death rates were calculated as the complement of the exponential of the slope of the least-squares line through the logarithms of the central death rates, multiplied by 100 to convert to percent form, and are given in Table 2. The sharpest reductions for the 1981 to 2001 period were in the categories of Heart Disease, averaging 2.1 percent and Vascular Disease, which averaged about 1.9 percent reduction per year. The categories of Violence and Cancer averaged 0.9 percent and 0.2 percent reduction per year, respectively. On the other hand, the categories Respiratory Disease, Diabetes Mellitus and the residual group of Other causes actually averaged an increase of about 1.1 to 2.5 percent per year.
Ultimate annual percentage reductions in central death rates by sex, age group, and cause of death were postulated for years after 2029. The broad age groups for which specific rates of reduction were selected are: under age 15, ages 15-49, ages 50-64, ages 65-84, and age 85 and older. The postulated ultimate annual percentage reductions are shown in Table 3.
Annual reductions in mortality by age, sex, and cause from 2001 to 2002 and from 2002 to 2003, were assumed to equal the average annual reductions observed for the period 1981-2001. For years after 2003, the reductions in mortality were assumed to change from initial levels of 100 percent of the average annual reductions observed for the period 1981-2001, to the postulated ultimate percentage reductions shown in Table 3, whenever these initial rates of reduction were positive. However, if the initial rates of reduction for a specific age, sex, and cause group were negative, the initial level was assumed to be 75 percent of the 1981-2001 average annual reduction. To move from the initial level to the ultimate percentage reduction, a relative decrease in the difference to the ultimate reduction is moved each year. The postulated ultimate percentage reductions were assumed to apply after the year 2029. Tables 4a and 4b show historical and projected age-adjusted central death rates by cause of death and sex for the period 1979-2100.
Even though ultimate annual percentage reductions in central death rates are postulated for the seven causes listed in Table 3, the resulting percentage reduction in age-adjusted central death rates for all causes combined are carefully reviewed, analyzed, and adjusted to assure consistency with the overall assumed rates of reduction. For each age and sex group, the decomposition of the percentage reduction by causes also provides a useful tool to test the reasonableness of the overall reduction.
V. Results
Tables 6 and 7 show values for the functions qx, lx, dx, Lx, Tx, and 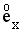 by age and sex for selected years. Table 6, the period table (by calendar year), presents values for every tenth year from 1900 through 2100. Table 7, the cohort table (by year of birth), includes every tenth year 1900 through 2100. The methods used to produce the values shown in these tables have been described in Section IV of this actuarial study.
by age and sex for selected years. Table 6, the period table (by calendar year), presents values for every tenth year from 1900 through 2100. Table 7, the cohort table (by year of birth), includes every tenth year 1900 through 2100. The methods used to produce the values shown in these tables have been described in Section IV of this actuarial study.
For each calendar year, or cohort, death rates are relatively high in the first year after birth, decline very rapidly to a low point around age 10, and thereafter rise, in a roughly exponential fashion, before decelerating (or slowing their rate of increase) at the end of the life span. Cohort tables show less rapid increase in the death rate with advancing age than do period tables because cohort tables reflect in succeeding ages the general improvement in health and safety conditions that occur over time. Conversely, period tables show more rapid increase in death rates with increasing age because calendar year experience for each higher age does not reflect the improved mortality of the succeeding years.
Table 8 presents a summary comparison of one-year probabilities of death for selected ages, by sex and calendar year. This allows a more detailed year-by-year analysis of the improvement in age specific death rates over time than was presented in Table 6. The greatest relative improvement in mortality during the twentieth century occurred at the young ages, resulting largely from the control of infectious diseases. For each sex, the probability of death at age 0 decreased 95 percent between 1900 and 2001 and a further reduction of about 83 percent is projected between 2002 and 2100. At age 30, the decrease between 1900 and 2001 was 83 percent for males and 92 percent for females, reflecting the rapid decline in childbearing mortality experience for females. Over the period 2002-2100, further decreases of 58 and 51 percent for males and females respectively, are projected.
At ages 60, 65, and 70, shown in Table 8, the probability of death decreased by about 55 percent for males and by over 65 percent for females between 1900 and 2001. Death rates are projected to decrease by about 55 percent for males and 50 percent for females in the 2002-2100 period. This large sex differential in mortality improvement is attributed partly to genetic factors and partly to environmental factors. If the genetic factors are more important, then the sex gap in mortality can be expected to remain large or even widen. If the environmental factors are more important, then the sex gap can be expected to close somewhat as women become increasingly subject to the same pressures and hazards as men. For example, during the period 1970 through 1980 when great strides were made in treating degenerative diseases affecting the cardiovascular system, male mortality at age 65 decreased 18 percent while female mortality decreased only 11 percent. Over the following 20-year period, from 1980-1999, male mortality at age 65 continued to decrease faster than female mortality, with male mortality decreasing 30 percent and female mortality decreasing only 13 percent. Increasing levels of tobacco use and job stress for women are expected to tend to narrow the gap in the future.
Table 9 presents a summary comparison of cohort qx's, one-year probabilities of death at selected ages by sex and year of birth. The values in this table are the same as those in Table 8; however, they are organized so that relative levels of death probability at each age can be conveniently compared across cohorts rather than across calendar years of experience.
Table 10 presents life expectancy at selected ages, by sex and calendar year on a period basis. That is, life expectancy at a particular age for a specific year is based on the death rates for that and all higher ages that were, or are projected to be, experienced in that specific year. Life expectancy at age 0 for males increased 27.7 years from 46.4 years in 1900 to 74.1 years in 2001. During the same period, life expectancy at age 0 for females increased 30.5 years from 49.0 years to 79.5 years. Thus the sex gap in life expectancy at birth has increased from 2.6 years in 1900 to 5.4 years in 2001. However, the sex gap has declined from a level of 7.8 years for 1973 and is projected to continue declining at a slow rate reaching a difference of 4.2 years in 2025.
Figure 2a shows life expectancy at age 0, by sex and calendar year, based on period life tables. Rapid gains in life expectancy at age 0 occurred from 1900 through the mid 1950's for both males and females. From the mid 1950's through the early 1970's, male life expectancy at age 0 remained level, while female life expectancy at age 0 increased moderately. During the 1970's faster improvement resumed for both males and females. Life expectancy for males and females in the 1980's improved only slightly with males improving more than females. In the 1990's, life expectancy has remained fairly constant for females, increasing only slightly for males.
Figure 2b shows life expectancy at age 65, by sex and calendar year, based on period life tables. Life expectancy at age 65 for males increased from 11.3 years in 1900 to 15.7 years in 2001, while for females the increase was from 12.0 years to 18.9 years. However, this sex gap diminished during the 1980's and 1990's and is projected to decrease only slightly in the future.
Little increase was experienced from 1900 to 1930. Since then, rapid gains occurred for females until the significant slowdown of the 1980's. The 1990's have been stable for females. For males, improvement has been rapid since the 1930's, but with a stable period during the 1950's and 1960's.
Table 11 shows, on a cohort basis, life expectancies at selected ages, by sex and year of birth. That is, life expectancy at a particular age for a specific year is based on death rates for that age in the specific year and for each higher age in each succeeding year. Life expectancies on a cohort basis tend to fluctuate less from year to year than do period-based life expectancies because of sudden and temporary events, such as a flu epidemic, which may affect the entire population, for a brief period of one or two years, but affect only one or two years of mortality experience for each of the cohorts alive during the period. Therefore, cohort life expectancies are more useful in analyzing subtle and gradual generational trends in mortality.
Figure 3a shows life expectancy at age 0, by sex and year of birth, based on cohort life tables. Life expectancy at age 0 for males increased 28.6 years from 51.5 years for births in 1900 to 80.1 years for births in 2001. During the same period, life expectancy at age 0 for females increased 26.0 years from 58.3 years to 84.3 years. Thus the sex gap in life expectancy at birth in a cohort has decreases from 6.8 years for births in 1900 to 4.2 years for births in 2001. However, substantial increases in the sex gap in life expectancy at birth were experienced during this period, reaching 7.5 years for births in 1920, followed by a gradual decline to the projected gap for births in 2001.
Figure 3b shows life expectancy at age 65, by sex and year of birth, based on cohort life tables. Life expectancy at age 65 for males is projected to increase from 13.5 years for males born in 1900 to 20.5 years for males born in 2001. During the same period, the life expectancy for females at age 65 is projected to increase from 18.0 years for females born in 1900 to 23.0 years for females in 2001. Thus the sex gap in life expectancy at age 65, on a cohort basis is projected to decrease from 4.5 years for those born in 1900 to 2.5 years for those born in 2001.
Table 12 presents ratios of female to male values for life expectancies and for one-year probabilities of death, for selected ages and calendar years, based on period life tables. These ratios provide another perspective from which to consider sex differences.
Table 12 shows that the ratio of female to male life expectancy generally rose fairly steadily from 1900 through 1979 at ages 0 through 70. This ratio has declined since 1979 and is expected to continue to decline at a slow rate in the future. This trend reflects the general decline through 1970 in the ratio of female to male death probabilities at the important ages 60 through 70, and the actual and projected increase, thereafter, in this ratio for these ages.
Table 12 also shows that the ratio of female to male life expectancy at age 100 was constant from 1900 through 1959 reflecting the fact that male and female death probabilities are estimated to have been essentially the same at this and higher ages throughout this period. Since 1959, however, the ratio of female to male life expectancy at age 100 has increased, and is projected to be around 1.15 after 2001.
Table 13 presents ratios of female to male values similar to those in Table 12, but based on cohort life tables. The ratio of female to male life expectancy declines steadily at ages 0 through 70, for cohorts born after 1906. This again reflects the increase throughout that period in the ratio of female to male death probabilities at the important early-elderly ages. Declines in the ratio of female to male life expectancy at age 100 reflect the past and projected increases in the ratio of female to male death probabilities at very high ages.
Table 14 presents the age for three selected survival rates, by sex and calendar year on a period basis. The median of the inverse survival distribution increased 22.6 years, from 55.2 years for males in 1900 to 77.8 in 2001. For females the increase was 24.6 years, from 58.2 years in 1900 to 82.8 years in 2001. Increases in life expectancy between 2002 and 2100 are projected to be 8.2 years for males and 6.2 years for females.
Figure 4a shows median lifetime by sex and calendar year, based on period life tables. The shapes of the survival function at S(x) = .5 are similar to the shapes of the life expectancy curves at age 0, except that increases are smaller.
Table 14 shows that for the survival rate = 0.00001, the corresponding age for males increased from 104.4 years in 1900 to 109.8 years in 2001, while for females it increased from 104.9 years to 112.0 years. From 2002 to 2100, the age for males is expected to increase by 8.2 years and for females by 7.3 years. This trend runs counter to the widely held belief that the age attained by the oldest survivors in the population has risen little, if at all, during the twentieth century.
Figure 4b shows the extreme old age, age x such that S(x) = 0.00001, by sex and calendar year, based on period life tables X, such that S(x) = 0.00001 increased very little from 1900 through 1930. Between 1930 and 1954, and again between 1963 and 1982, saw a rapid increase in age. Since 1982, age x for S(x) = 0.00001 has decreased for both males and females. For the period 2001-2100, x such that S(x) = 0.00001 is projected to briefly continue to decline then begin to rise steadily and slowly at about 0.1 year per year for males and 0.05 year per year for females.
Figure 5 presents the population survival curves based on period life tables for selected calendar years. Great strides were made in the twentieth century toward eliminating the hazards to survival which existed at the young ages in the early 1900's. Very little additional improvement to survival rates is possible at these young ages. Survival rates at the older ages are projected to continue to improve steadily. Projected gains in the probability of surviving to age 90 during the next 50 years are about the same as experienced during the past 50 years. For age 100, projected gains are much greater than for the past. Figure 5 shows population survival curves based on period life tables for, from left to right, 1900, 1950, 2000 and projected years 2050 and 2100.
Although the shape of the survivorship curve has become somewhat more rectangular (less diagonal) through time, it appears that very little additional rectangularization will occur because survival rates are already so high at the young ages and are expected to continue increasing at older ages. The so-called "curve squaring" concept, though appealing to many, simply cannot be supported by the mathematics of mortality. The age at which the survivorship curve comes close to zero, through the compounding of single-year probabilities of survival, has increased greatly during the twentieth century and will continue to increase, as further strides are made against degenerative diseases. That mortality rates are found to continue to decline, at every age for which adequate data are available, demonstrates that no absolute limit to the biological life span for humans has yet been reached, and that such a limit is unlikely to exist.