This study is based on over 11.9 million records of Social Security Disability Insurance (DI) worker beneficiaries drawn from the administration’s Master Beneficiary Record (MBR) in February 2009. The 5-year observation period covers January 1, 2001 through December 31, 2005. These records provide 25.5 million life-years of exposure for males and 20.4 million life-years of exposure for females. The primary variables of interest are: the reason for termination of benefits, the age at entitlement, the number of years since entitlement, and sex of the beneficiary.
There are a small number of terminations due to other reasons that are not explicitly examined. The table below provides the number of deaths and recoveries observed during the observation period. To a certain extent, this study traverses the activity of the OASI rolls by tracking deaths of former disabled workers who converted to old-age worker benefits either by choice or upon attaining normal retirement age.
Source: MBR database as of February 2009. Refer to table 5 in section IV for the number of conversions and terminations due to other reasons. The number of deaths and recoveries shown above will differ from those found in table 5 due to differences in statistical methods used in tabulations. The number of deaths will be dramatically different as they include a substantial number from the OASI rolls.
Mortality experience of the DI rolls is affected by several unique circumstances. Since experience begins with entitlement, deaths that occur during the 5-month waiting period prior to entitlement to DI benefits are outside the scope of this study. It is also true that a claimant may die in the first month of entitlement, or before final disposition of the disability claim—in which case only retroactive disability benefits may be payable. These cases are handled by counting the death, but crediting no exposure on the record.
Up to three separate periods of disability are examined for participants in this study. There are instances, however, where very little time passes between periods of entitlement for reasons such as a failed work-attempt, an expedited reinstatement, or a successful appeal of an unfavorable CDR. So although a recovery has occurred, the beneficiary may be back on the rolls shortly thereafter. Also, it is not uncommon for beneficiaries with multiple periods of disability to become re-entitled under the same or a similar impairment. Although re-entering the rolls at a different select age, such individuals may, in essence, recover from the same disability more than once.
After various screenings and checks, data for up to three separate periods of disability were included for the following beneficiaries in the final overall sample:
Records of persons from the Special Disability Workload (SDW) were excluded from this study. This group of SSI recipients who are potentially eligible for DI benefits due to previously unrecognized disability-insured status caused a supplemental increase in awards beginning in 2001. In most instances, entitlement is retroactive to well before the date of final review. However, due to the guidelines established for processing the workload, completed SDW cases represent a biased sample of records and were therefore eliminated.
The availability of complete data on each person in the study (sex, date of birth, date of entitlement, date of decrement, and cause of decrement) allows for direct estimation of the
multiple-decrement probabilities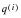 
, where
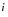
represents the cause of decrement. Each unit age interval
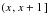
represents one life-year of potential exposure. For each interval that an individual is under observation, the person enters the interval at age
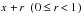
, and is scheduled to exit the interval at age
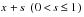
. Note that
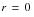
except for instances where the beginning of the observation period falls within the age interval. Similarly
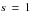
except for instances where the end of the observation period falls within the interval. Clearly,
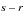
is the amount of time that the person is scheduled to be exposed to the risks of decrement. The total
scheduled exposure for an interval is obtained by summing over all persons.
1
As an example of the above method, consider a disabled worker entering an interval at age
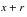
. The
scheduled ending age,
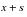
, is established for the interval under the expectation that the person will either survive to the end
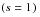
, or exit the study due to the end of the observation period
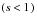
. Scheduled exposure is then credited as follows: if the person survives to the end of the interval, then exposure is credited from
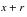
to
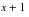
; if the person dies or recovers during the interval, exposure is still credited from
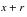
to
;
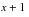
2 if the observation period ends during the interval, then exposure is credited from
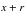
to
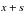. A modification is made to the way exposure is calculated for determining recovery probabilities. Since recovery is no longer a consideration after converting to old-age benefits, exposure is credited only up until the month of the switch.
Multiple-decrement probabilities are calculated by dividing the observed number of deaths or recoveries in an interval by the aggregate scheduled exposure for that interval. As will be discussed later,
single-decrement (absolute) rates can be derived from these probabilities by using a constant force assumption for the distribution of decrement within the interval.
3
This is a select-and-ultimate study with a 10-year select period implying that the risks of decrement for beneficiaries 10 or more years beyond selection are no longer a function of select age, but a function of attained age only.
Rarely does entitlement to disability benefits occur on a beneficiary’s birthday. To facilitate exposure calculations,
insuring age and the corresponding
insuring date of birth may be substituted for the actual age at entitlement and the actual date of birth, respectively. This study uses an insuring age that is set at the beneficiary’s
age last birthday as of entitlement. As an example:
Use of insuring age results in an integral select age at entitlement, ensuring that subsequent durations begin on the beneficiaries birthday. This is true whether the participant enters the study during the observation period, or is already part of the entitlement group when the observation period opens.
The unit intervals for which a beneficiary is under observation are called
durations. For each select age
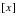
and duration
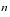
, the quantity
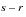
represents the amount of exposure contributed to the observation interval
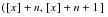
. For durations beyond the 10-year select period, exposure is credited to the appropriate attained age interval
.
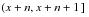
The select-and-ultimate multiple-decrement probabilities are graduated using the two-dimensional Whittaker-Henderson Type B method .
4 The horizontal and vertical smoothing coefficients were chosen to obtain some degree of smoothness within individual durations (columns) as well as within select ages (rows), without deviating much from the original estimates.
Survival tables 8A-8C are constructed from select-and-ultimate death probabilities. The values
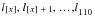
are first calculated for select age
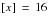
, using a radix of 100,000. This step determines values for the ultimate period of the table and attained ages greater than 75. Values for select ages
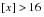
are then derived from the ultimate values by working backwards. For example,
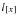
is determined from
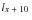
using the survival probabilities of the select period for the given select age. The value for
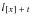
is the number of lives remaining from the original
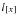
who have attained age
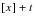
. The number alive at any given select or attained age is not an actual count of disability beneficiaries, but is the product of combining probabilities with an arbitrary radix.
Survival tables for the decrement of recovery (15A-15B) and the combined decrements of death and recovery (22A-22C) are constructed in the same manner. Since recovery is no longer considered after attaining normal retirement age, tables 15A-15B are truncated after attained age 65.
5
The survival tables are read across the row, or select period, for 0-10 years since selection, then down the last column, or
ultimate period for 10 or more years since selection. The example below uses numbers from table 8A for male beneficiaries disabled at select age 50.
Expected future lifetime tables are derived from the survival functions described above using the basic actuarial principles found in any standard actuarial text on life contingencies. We also present in this study the results of aggregating over duration, by select age (see tables 11, 18, and 25) or attained age (see tables 12, 19, and 26).
Expected future lifetime for a specific select age is an exposure-weighted average of the expected future lifetime at each duration of that age. This differs from the expected lifetime for a specific
attained age, which is an exposure-weighted average of the expected future lifetime of various durations.
For example, expected future lifetime for select age 40 is a weighted average of the expected lifetimes shown across the select row and down the ultimate column. In this instance, each cell represents a different attained age. In contrast, expected future lifetime for
attained age 40 is the average of the expected lifetimes for a select 40‑year-old at duration 0, a select 39-year-old at duration 1,... a select 16-year-old at duration 24—all of whom are attained age 40.
In this study we present probabilities of decrement for two of the several decrements affecting the disabled population—death and recovery. The symbol
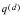
represents the probability of death in the presence of the other decrements and is defined as follows:
where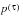 
is the probability of surviving under all decrements; and
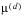
is the force of mortality. The probability of recovery
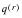
is similarly defined.
For each cause of decrement in a multiple-decrement model, it is possible to associate a single-decrement rate that depends only on a particular cause of decrement. For example,
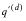
represents the
single-decrement (absolute) rate of death and is defined as follows:
where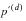 
is the probability of not dying. In this representation, beneficiaries who decrement for causes other than death are “taken out” of the total number exposed. Observation stops at the point of non-death decrement resulting in total exposure which is somewhat less than that used in formulating death probabilities.
For example, the multiple-decrement probability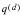 
is calculated for each combination of select age and duration by dividing the observed number of deaths by the exposure for that cell. Assuming a uniform distribution for each decrement over the age interval
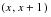
, the absolute rate of death
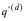
can be calculated by dividing the observed number of deaths by the exposure for that cell reduced by one-half of the number of recoveries observed for that cell. The absolute rate of recovery
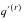
is similarly defined.
A life annuity is a series of payments made at regular intervals (such as months or years) during the lifetime of the annuitant. Payments may be limited to a given number of years, or payable for the whole of life, and are made at the beginning (
due) or end (
immediate) of each period. Any standard actuarial text on life contingencies will explain the present value calculation of an annuity.
The table below shows the present value of a whole-life annuity due and a temporary life annuity due to age 66 for a male worker disabled at age 50.
:
A life annuity is a series of payments made at regular intervals (such as months or years) during the lifetime of the annuitant. Payments may be limited to a given number of years, or payable for the whole of life, and are made at the beginning (due) or end (immediate) of each period. Any standard actuarial text on life contingencies will explain the present value calculation of an annuity.The table below shows the present value of a whole-life annuity due and a temporary life annuity due to age 66 for a male worker disabled at age 50.. The important point is that decrement was not expected so the scheduled ending age is set at
.
= 
= 
