A Stochastic Model
of the Long-Range Financial Status
of the OASDI Program—September 2004





 |
 |
 |
 |
 |
|
V. APPENDICES
Time-Series Modeling
Time-series analysis is a standard projection technique in econometric modeling. The equations used to project the assumptions are fit using these techniques. This appendix provides details about the models in general, presents statistical methods employed to test these models, and underscores the nuances inherent in the method of determining the equations. The reader may wish to consult Box, Jenkins and Reinsel (1994) or Hamilton (1994) for a standard presentation of this material. A more elementary reference is Pindyck and Rubinfeld (1998).
Stationary Time Series
A time series Yt is stationary if neither the mean nor variance depends on time t:
In particular, the variance of Yt is always equal to σ2 = γ0 . A different concept is that of strict stationarity. This means that any k values of the time series have the same joint distribution as any other set of k values of the time series. If a time series Yt is strictly stationary, then it is stationary. Henceforth, when we say that a time series Yt is stationary we intend that it is strictly stationary. However, it is more straightforward to think of a time series as stationary in the simpler sense.
White Noise Process
Suppose that εt, the error term at time t, is normally distributed with mean zero and constant variance σε2. If εr and εs are uncorrelated for r ≠ s, then the series εt is called a white noise process.
Random Walk
The simplest of all time-series models is the random walk. Here, if Yt is the series to be estimated, then the random walk process is given by Yt = Yt-1 + εt . The error term series, εt , is a white noise process. The forecast error variance increases as a linear function of the forecast lead time, l. In other words, the variance of the l-step-ahead forecast error is lσε2. The confidence intervals for these forecasts will therefore widen as l increases.
Moving Average (MA) Models
A time series is called a moving average model of order q, or simply an MA(q) process, if
Yt = µ + εt –θ1εt-1 –θ2εt-2 –…–θqεt-q .
In this equation, θ1,…,θq are constant parameters and µ is the process mean. The error term series, εt, is a white noise process.
Autoregressive (AR) Models
A time series is called an autoregressive model of order p, or simply an AR(p) process, if
Yt = φ1Yt-1 + φ2Yt-2 +…+φpYt-p + δ + εt .
In this equation φ1,…,φp are constant parameters and δ is a drift term. The naming of this model is apt because the coefficients of the time-series equation are obtained by regressing the equation on itself, more precisely, with its own p lagged values. The error term series, εt, is a white noise process. If this time series is stationary, then the mean μ of this process is computed to be
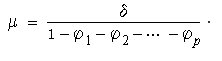
Autoregressive Moving Average (ARMA) Models
As its name indicates, an autoregressive moving average model of order (p,q), or simply an ARMA(p,q) model, is a natural combination of an autoregressive and moving average model. The equation which specifies an ARMA(p,q) model takes the form
Yt = δ + φ1Yt-1 + φ2Yt-2 +…+ φpYt-p + εt –θ1εt-1 –θ2εt-2 –…–θqεt-q .
Deviations Form of ARMA Model Equations
It is often more convenient to transform an ARMA model equation into deviations form using the equation
yt = Yt – μ,
where μ is defined, as above, to be the mean of the process. The transformed model may be written as
yt = φ1yt-1 + φ2yt-2 +…+ φpyt-p + εt –θ1εt-1 –θ2εt-2 –…–θqεt-q ,
and has a mean of zero.
Adding the original process mean to both sides of the equation produces
Yt = μ + φ1yt-1 + φ2yt-2 +…+ φpyt-p + εt –θ1εt-1 –θ2εt-2 –…–θqεt-q .
The lagged variables are left in deviations form, and the constant term, μ, on the right-hand side is the process mean.
Cholesky Decomposition
Suppose 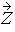 = (Z1,…, Zn)´ is a vector of independently and identically distributed standard normal random variables.
(If A is a matrix, then A´ denotes its transpose.)
Suppose we want to use these random variables to obtain a random vector
= (Z1,…, Zn)´ is a vector of independently and identically distributed standard normal random variables.
(If A is a matrix, then A´ denotes its transpose.)
Suppose we want to use these random variables to obtain a random vector
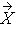 = (X1,…, Xn)´ from a multivariate normal distribution with mean
= (X1,…, Xn)´ from a multivariate normal distribution with mean
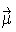 = (µ1,…, µn)´ and an n×n variance-covariance matrix V = (σij)
[with σij = Cov(Xi, Xj) for i, j = 1,…, n].
Since V is positive definite and symmetric, a standard result in linear algebra yields a lower triangular matrix, L, such that V = LL´.
The random vector X =
= (µ1,…, µn)´ and an n×n variance-covariance matrix V = (σij)
[with σij = Cov(Xi, Xj) for i, j = 1,…, n].
Since V is positive definite and symmetric, a standard result in linear algebra yields a lower triangular matrix, L, such that V = LL´.
The random vector X = 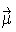 + L
+ L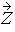 is then a random vector with the desired properties.
The decomposition V = LL´ is called a Cholesky decomposition; see Atkinson (1989) for more details. In what follows we call the matrix L a Cholesky matrix.
is then a random vector with the desired properties.
The decomposition V = LL´ is called a Cholesky decomposition; see Atkinson (1989) for more details. In what follows we call the matrix L a Cholesky matrix.
For our applications, a Cholesky decomposition is used to convert a random vector, 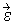 of independent standard normal variates to a multivariate normal distribution with mean
of independent standard normal variates to a multivariate normal distribution with mean
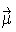 =
= 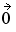 (the zero vector) and a variance-covariance matrix V obtained by using historical data.
If L is a lower triangular Cholesky matrix associated with V then the vector
L
(the zero vector) and a variance-covariance matrix V obtained by using historical data.
If L is a lower triangular Cholesky matrix associated with V then the vector
L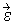 has the required multivariate normal distribution.
has the required multivariate normal distribution.
Vector Autoregressive Models
Vector autoregressive models allow the joint modeling of time-series processes. For the sake of simplicity, suppose that three variables y1,t , y2,t , and y3,t depend on time t. Data may indicate that these variables may be related to each other's past values. The simplest such case is when the relationship is limited to the time-1 lag, i.e., when y1,t , y2,t , and y3,t may be modeled in terms of y1,t-1, y2,t-1, and y3,t-1. In this case, a three-variable VAR(1) model takes the form
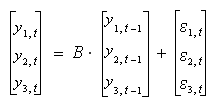
for some 3×3 matrix B.
Alternatively stated, if 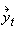 = (y1,t, y2,t, y3,t)´
and
= (y1,t, y2,t, y3,t)´
and 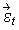 = (ε1,t, ε2,t, ε3,t)´
then the model takes the form
= (ε1,t, ε2,t, ε3,t)´
then the model takes the form 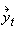 =
= 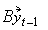 +
+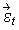 for some 3×3 matrix B.
for some 3×3 matrix B.
The k-variable VAR(p) model, with p lags, naturally extends from this.
If 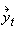 = (y1,t, y2,t,…, yk,t)´
and
= (y1,t, y2,t,…, yk,t)´
and 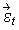 = (ε1,t, ε2,t,…, εk,t)´,
then the k-variable VAR(p) model takes the form
= (ε1,t, ε2,t,…, εk,t)´,
then the k-variable VAR(p) model takes the form
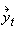 =
= 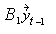 +
+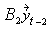 +…+
+…+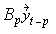 +
+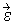 for k×k matrices B1,…, Bp.
for k×k matrices B1,…, Bp.
Modified Autoregressive Moving Average (ARMA) Models
The equations used to model the assumptions are autoregressive moving average models with the additional requirement that the mean of the variable Yt is always equal to its value under the TR04II. The value of the variable under the TR04II is written YtTR. Thus, the mean of Yt varies, in general, in the early years of the long-range period. The resulting model is called a modified autoregressive moving average model. In general, the equation in a modified autoregressive moving average model takes the form
Yt = δt + φ1Yt-1 + φ2Yt-2 +…+ φpYt-p + εt –θ1εt-1 –θ2εt-2 –…–θqεt-q .
Writing this equation in "deviations form," with yt = Yt – μt gives
Yt = μt + φ1yt-1 + φ2yt-2 +…+ φpyt-p + εt –θ1εt-1 –θ2εt-2 –…–θqεt-q .
Since μt = YtTR, we obtain the expression
Yt = YtTR + φ1yt-1 + φ2yt-2 +…+ φpyt-p + εt –θ1εt-1 –θ2εt-2 –…–θqεt-q .
Equations in Chapter II are all presented in this form, with the letters Y and y replaced with a more suggestive naming.