A Stochastic Model
of the Long-Range Financial Status
of the OASDI Program—September 2004





 |
 |
 |
 |
 |
|
V. APPENDICES
A standard reference for this appendix is Knuth (1997). In choosing a random number generator, it is essential to make the following considerations:
Given a seed I0 and a judicious choice of a and m, the linear congruence Ij+1 = aIj (mod m) will generate a sequence of numbers. The values a = 16,807 and m = 231 – 1 have the property that, for any nonzero initial seed, a large number of variables may be generated before cycling occurs. Upon division by m, a sequence of variates Uj of a uniform distribution on the interval (0,1) is generated. This linear congruential generator with these values of a and m is the so-called "Minimal Standard" generator of Park and Miller and appears in Press et al. (2001). As explained there, the value of 0 must never be allowed as the initial seed. Also, since a and m are relatively prime, the value of 0 will never occur provided that the initial seed is nonzero. This choice of a and m gives a cycle of maximum possible length 231 – 2. The Minimal Standard generator can be modified so as to remove low-order serial correlations inherent in the random numbers produced by that method. The method is adapted from Press et al. (2001) and uses the Park-Miller algorithm along with a Bays-Durham shuffle. This is the process we used to generate uniform (0,1) variates. There are other methods which will further eliminate such serial correlations. We chose this particular method to balance the need to remove such serial correlations with the expense of run-time.
To generate the standard normal (mean 0 and variance 1) variates used to generate the random error terms for our equations, one may transform uniform variates using the Box-Muller method: generate two independent uniform (0,1) variates, U1 and U2 , and compute
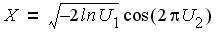 and
and 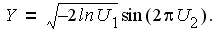 In order to avoid the use of trigonometric functions, we instead used the Polar method.
This, as a preliminary step, transforms the two uniform (0,1) variates U1 and U2 to uniform (-1,1) variates V1 and V2 (using the transformation V = 2U + 1).
If S = V12 + V22
then
In order to avoid the use of trigonometric functions, we instead used the Polar method.
This, as a preliminary step, transforms the two uniform (0,1) variates U1 and U2 to uniform (-1,1) variates V1 and V2 (using the transformation V = 2U + 1).
If S = V12 + V22
then 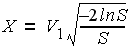 and
and 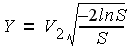 will be two independent random draws from a standard normal distribution, provided that S is less than one.
(If not, then we repeat this process until it is.)
Although this method produces two standard normal variates, we always used the first one (X) and discarded the second one (Y).
Each equation for each assumption is separately seeded to have its own random number stream.
will be two independent random draws from a standard normal distribution, provided that S is less than one.
(If not, then we repeat this process until it is.)
Although this method produces two standard normal variates, we always used the first one (X) and discarded the second one (Y).
Each equation for each assumption is separately seeded to have its own random number stream.