Discount Rate Specification and the Social Security Claiming Decision
Social Security Bulletin, Vol. 76 No. 2, 2016 (released May 2016)
Choosing the claiming age that maximizes the expected present value of lifetime Social Security retirement benefits requires, among other criteria, the specification of a rate to use when discounting the future benefit payments for each claiming age. Although some experts maintain that the only appropriate rate is the current yield on long-term government bonds, a more appropriate rate choice would reflect the particular needs of a given individual. This article evaluates optimal claiming ages for prospective beneficiaries over a range of real discount rates from 0 percent to 8 percent, considering the survival functions for men and women born in 1952. Viewed prospectively, the optimal claiming age is older at lower discount rates and younger at higher rates. In addition, the risk that the optimal claiming age will ultimately fail to maximize lifetime benefits is highest at low discount rates and declines as the discount rate increases.
Brian Alleva is with the Office of Retirement Policy, Office of Retirement and Disability Policy, Social Security Administration.
Acknowledgments: I thank Chris Anguelov, Richard Chard, David Rajnes, Robert Weathers, Marni Cooper, Natalie Lu, and Mark Sarney for their helpful comments and suggestions.
Contents of this publication are not copyrighted; any items may be reprinted, but citation of the Social Security Bulletin as the source is requested. The findings and conclusions presented in the Bulletin are those of the author and do not necessarily represent the views of the Social Security Administration.
Introduction
| EOL | expected opportunity loss |
| FRA | full retirement age |
| MCA | maximizing claiming age |
| OCA | optimal claiming age |
Although a covered worker can claim Social Security retirement benefits when reaching age 62, the monthly benefit amount increases incrementally with every month claiming is delayed up to age 70. Once started, benefits continue essentially unchanged, in real terms, for the participant's remaining lifetime. For any given individual, the optimal claiming strategy will depend on many factors, as personal circumstances and retirement goals vary widely. If one's goal is to maximize total lifetime benefits, that individual must determine the optimal claiming age (OCA), or that which maximizes the expected present value of the lifetime benefit stream.
Beyond accounting for the myriad program rules affecting the decision to claim, choosing the optimal age requires two input criteria that can be difficult to determine. First, gauging the probability-weighted duration of the benefit stream for each possible claiming age, and thus its expected present value, requires a survival function or similar specification to indicate the participant's longevity prospects. Second, a discount rate is required to account for the time value of money when converting the future benefit stream for each claiming age into aggregate lifetime amounts for comparison. This article focuses on the second requirement with a sensitivity analysis that covers a full range of plausible discount rates for single participants born in 1952. This study does not advocate the use of any particular discount rate or any criterion for choosing one, but does examine the implications of one's choice of rate and the precision of that rate specification.
Many studies of the claiming decision use a single discount rate for all computations (Sun and Webb 2011; Shoven and Slavov 2014a, 2014b; Friedman and Phillips 2008; Meyer and Reichenstein 2010, 2012). Those studies share the rationale that the single discount rate should be related to the yield on long-term inflation-indexed government bonds because Social Security benefits are also inflation-adjusted financial obligations of the U.S. government and should thus be valued similarly. More specifically, those studies suggest that the bond yield prevailing at the time of the claiming decision (instead of perhaps the long-term average) should be used as a proxy for the cost of an equivalent guaranteed annuity purchased on the private market. Shoven and Slavov (2014a, 2014b) also examine how the OCA for different cohorts has changed along with the prevailing rate over time.
In some cases, it may be entirely reasonable to value the benefit stream with a discount rate much like that for a very low-risk government bond. Using such a rate is appropriate for valuing system liabilities (aggregate future benefits to all potential recipients) from the supply-side perspective of an insurer. In fact, the average long-term government bond rate is the cost of capital to the Social Security trust funds that the program's actuaries use in their annual assessments of system health.1 However, the insistence on discounting an individual's benefits by the yield on instruments of similar credit risk is somewhat misplaced, as it may prevent some participants from correctly valuing their potential benefit streams and, consequently, from optimizing their claiming ages. One participant may value a given potential benefit stream entirely differently from another. If Social Security benefit streams could be packaged and sold on the capital markets, then market pressure would quickly force the pricing of the credit-risk component to reflect equivalent government-bond yields. But entitled Social Security benefits are not a tradable security subject to market valuation. The claiming decision poses 97 monthly choices between ages 62 and 70, each with a different guaranteed fixed future cash stream that can be appropriately valued by the participant for whatever reason and according to how much more he or she values sooner payments rather than later ones. In addition, restricting the discount rate to interest rates current at the time of the decision, thus pricing the benefit stream against an equivalent annuity on the private market, would be relevant only to a participant who is actually seeking such an annuity. As Social Security is a compulsory program, participation alone does not indicate willingness to purchase more of a similar instrument.
Some studies do compare results for several discount rates (Coile and others 2002; Shoven and Slavov 2014b; Sun and Webb 2011; Sass, Sun, and Webb 2013; Alleva 2015). Taking an alternative approach and valuing the benefit stream as an investable asset, Spitzer (2006) and Manakyan, Ervin, and Claggett (2014) use stochastic simulations of benefit payments invested in portfolios with various allocations of stocks and bonds to explore the likelihood that one claiming age will produce higher lifetime benefits than another. These authors apply rate-of-return probability distributions that are more realistic than single-point estimates. Nevertheless, their results for stock-heavy portfolios with higher expected rates of return generally correspond with results from the studies using higher single-point discount rates, and their results for bond-heavy portfolios similarly correspond with those using lower single-point discount rates. In general, when the claiming-age objective is maximum expected lifetime benefits, these studies clearly confirm that lower discount rates prescribe delayed claiming and that higher rates prescribe earlier claiming.
With that conclusion established, the present study examines the sensitivity of the claiming decision to the discount rate, with several interesting results. First, the OCA at lower rates (typified by the expected returns of bond- and cash-heavy asset allocations) carries an elevated risk of generating lifetime benefit amounts that fall short of the maximum amounts that could be attained by the eventual age at death. However, that risk is not particularly sensitive to rates specified within this lower range, implying that conservative discounters need not specify a precise rate to materially affect the likely outcome. On the other end of the spectrum, aggressive discounters who use higher rates (representing, for example, the expected returns of stock-heavy asset allocations) will be far more confident in their decision, as the resulting OCA poses little risk of failing to maximize lifetime benefits. In addition, the OCA has essentially no sensitivity to the discount rate in this higher range: For individuals born in 1952 and discount rates of at least 3.8 percent for men and 4.6 percent for women, 62 is always the OCA, with the risk of failing to maximize lifetime benefits decreasing as the rate increases. For those who specify more moderate discount rates (broadly representative of an equal mix of stocks and bonds), both the OCA and its non-maximization risk are very sensitive to discount rate variations, with the optimal age dropping from near 67 to 62 for both sexes in less than 100 basis points (or 1 percentage point) of discount-rate change. Extra care should thus be taken with rate specifications in this middle range.
Methods
This study builds on Alleva (2015), which defines the maximizing claiming age (MCA) as that with which a participant of a given birth year, a given age at death, and a given discount rate will have the highest aggregate lifetime benefit. Of course, without knowing one's death age in advance, a participant must calculate lifetime benefits for each claiming age based on his or her survival function; that is, the probability of surviving to each possible age of death beyond 62.2 The OCA thus maximizes the expected present value (EPV) of lifetime benefits according to the survival function. The opportunity loss for a given death age is defined as the difference between the present values of lifetime benefits under the MCA and the OCA. In other words, although the OCA maximizes expected lifetime benefits, it may not ultimately maximize actual lifetime benefits. Consequently, the expected opportunity loss (EOL), which can be thought of as the risk in the decision, is the survival-weighted mean opportunity loss over all possible death ages for the given OCA. EOL is expressed as the present-dollar value of potential opportunity loss per dollar of the primary insurance amount, or the benefit amount to which a worker is entitled at full retirement age (FRA). The sum of the EPV and the EOL for each possible claiming age is a constant and thus the OCA, having the maximum EPV, by definition also has the minimum EOL (or risk) of any claiming age.3 Even so, the minimum EOL itself could be substantial, and when accounting for the full retirement period from age 62 to a maximum attainable age of 120, it is also quite unlikely that a calculated OCA will ultimately turn out to have matched the MCA (Alleva 2015, Exhibit 7).
In this study, MCA, OCA, and EOL computations for men and women born in 1952 at current age 62 are performed across the range of real annual discount rates from 0 percent to 8 percent, inclusive, specified in tenths of a percent for a total of 81 rates. For every rate, the MCA is computed for each age of death from 62 to 120 according to the claiming rules that apply to the 1952 cohort. Survival functions are then applied to compute the OCA and EOL separately for men and women at each rate. The computations cover all monthly death and claiming ages. In all expositions, age is expressed in the format years:months, such that 67 years and 4 months is expressed as 67:04 and exact age 62 is 62:00.
According to the survival function for men born in 1952 at current age 62 with a discount rate of 2.9 percent, there is a 36 percent probability that the MCA will be 62:00 and a 20 percent probability that the MCA will be 70:00; thus, the probability that the MCA will be some age in between is 44 percent. For women, the respective probabilities are 27 percent, 30 percent, and 43 percent (Alleva 2015). Notable among these MCA probabilities is the dominance of ages 62:00 and 70:00, which together account for more than half of the entire likelihoods, versus the other 95 monthly claiming ages combined. These probability distributions change dramatically with different discount rates, yet one or both of those two exact ages dominate the probabilities for most rates. For that reason, data for MCAs in this article are aggregated into five categories: exact age 62:00, exact age 70:00, and age ranges 62:01–63:00, 63:01–66:00, and 66:01–69:11. The three age ranges correspond to break points in the formula for determining the benefit amount based on claiming age for a member of the 1952 birth cohort. The benefit amount increases by 5⁄12 of 1 percent of the primary insurance amount for each month of delay after 62:00 through 63:00, by 5⁄9 of 1 percent for each month after 63:00 through 66:00 (the FRA), and by ⅔ of 1 percent per month after FRA up to (and including) 70:00 (see Alleva 2015).
The spectrum of real discount rates used in this study can be conveniently partitioned in terms of the expected real rates of return on portfolios of various allocations to stocks, bonds, and cash. This approach is relevant to participants who might have retirement savings invested in such portfolios, as drawing Social Security benefits for consumption would allow an equal amount to remain in the investment account, possibly continuing long-term accumulation around its expected rate of return. According to Ibbotson Associates (2011, 59–62), the historical compound real rate of return (annualized geometric average) is 6.7 percent for large-company stocks, 2.4 percent for long-term government bonds, and close to 0 percent for cash.4 As historical averages, these rates of return of course do not guarantee future results, but they serve as useful reference points for the long-term expected performance of commonly held asset classes. Using these historical returns as a guide, very low discount rates (below 2.4 percent) are indicative of very conservative discounters with portfolios comprising only cash and bond allocations. Relatively low discount rates (2.4 percent to about 4.6 percent) are indicative of conservative discounters with bond-heavy stock and bond portfolios. Balanced allocations near half stocks and half bonds with an average yield of about 4.6 percent indicate moderate discounters. Relatively high discount rates (about 4.6 percent to 6.7 percent) are indicative of aggressive discounters with stock-heavy portfolios. Very high discount rates (above 6.7 percent) are indicative of very aggressive discounters with portfolios of highly risky assets. Table 1 summarizes the discount rate partitions used in this analysis.
| Category | Range (%) | Investment strategy | Typical portfolio allocation |
|---|---|---|---|
| Very low | rd < 2.4 | Very conservative | Cash and bonds |
| Low | 2.4 ≤ rd < 4.6 | Conservative | Primarily bonds, some stocks |
| Moderate | rd ≈ 4.6 | Balanced | 50/50 stocks and bonds |
| High | 4.6 < rd ≤ 6.7 | Aggressive | Primarily stocks, some bonds |
| Very high | rd > 6.7 | Very aggressive | All stocks and other highly risky assets |
| SOURCE: Author's definitions based on Ibbotson Associates (2011). | |||
Results and Analysis
This section describes the findings for three primary objectives. The first objective is to determine the MCA as identified retrospectively. The second objective is to replicate the challenge that actually faces workers nearing retirement: to determine the OCA and the EOL prospectively. The third objective is to characterize the discount rate implied by a given OCA selection.
Retrospective MCA
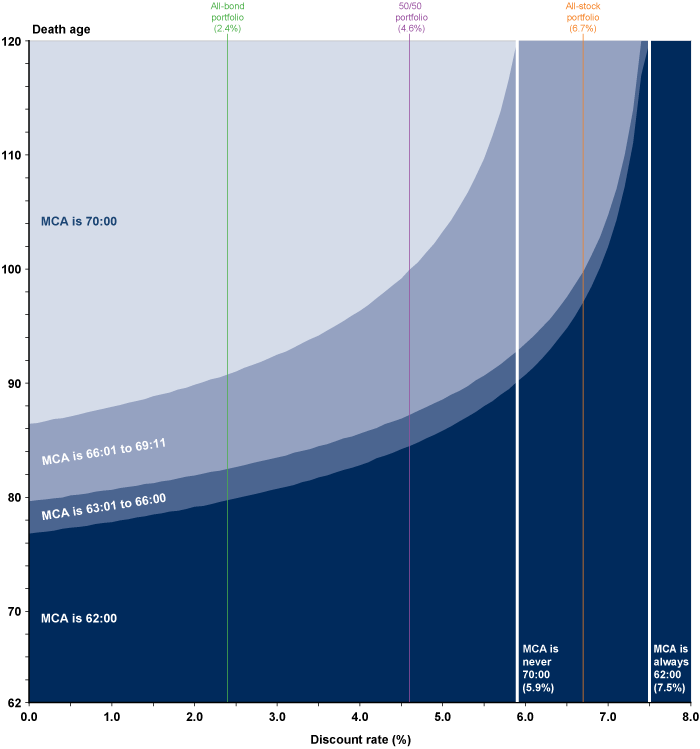
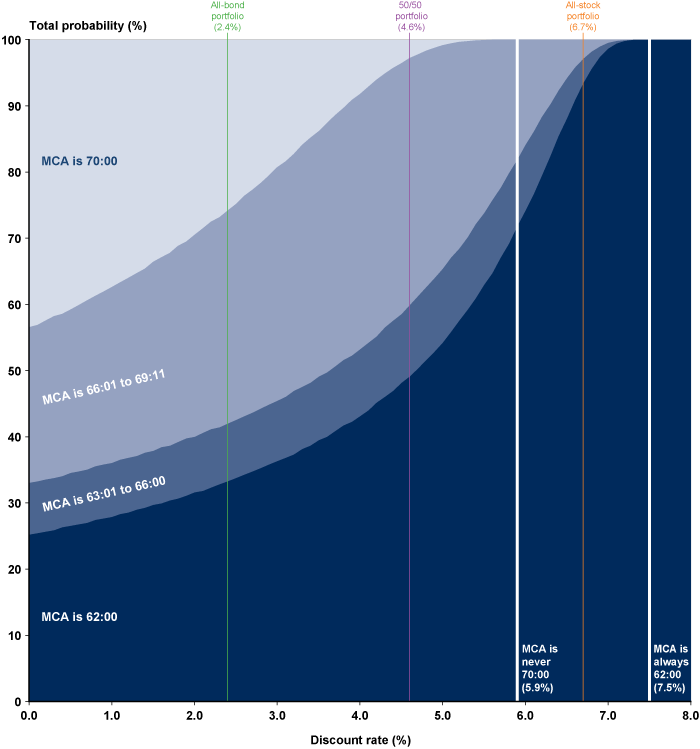
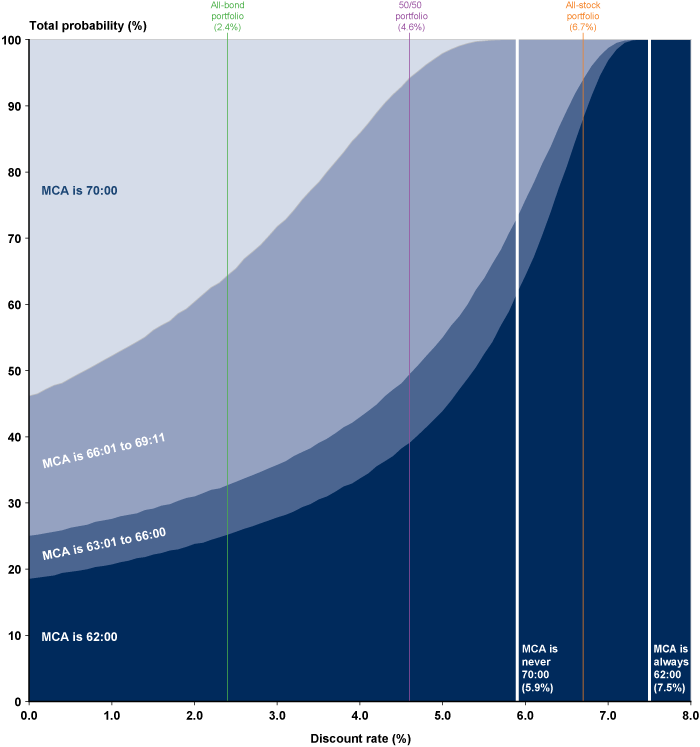
Chart 1 shows the death-age boundaries of the MCA categories for the entire 1952 cohort across the full spectrum of discount rates. Because the MCA computation is independent of survival probability, the figures in Chart 1 apply to both men and women. However, Charts 2 and 3 do use the separate survival functions respectively for men and women to show the actual MCA probability distributions. The plots for Charts 2 and 3 are similar, deviating only because of the difference in survival functions between the sexes. Because the MCA increases monotonically from younger death ages to older ones, the probabilities in Charts 2 and 3 for the older MCAs correspond to the probabilities of older survival ages. Expected returns for the representative investment portfolios are indicated by vertical lines. Table 2 lists details for each discount rate, including the death-age boundaries of each MCA category and the MCA probability distributions by sex.
Death-age boundaries for MCA categories, by discount rate: 1952 birth cohort (either sex)
| Discount rate (%) | Probability (in percent) that the MCA is— | |||
|---|---|---|---|---|
| 62:00 | 63:01–66:00 | 66:01–69:11 | 70:00 | |
| 0.0 | 76:09 | 79:08 | 86:05 | 120:00 |
| 0.1 | 76:11 | 79:09 | 86:06 | 120:00 |
| 0.2 | 77:00 | 79:09 | 86:08 | 120:00 |
| 0.3 | 77:00 | 79:11 | 86:09 | 120:00 |
| 0.4 | 77:03 | 80:00 | 86:11 | 120:00 |
| 0.5 | 77:03 | 80:02 | 87:00 | 120:00 |
| 0.6 | 77:05 | 80:03 | 87:03 | 120:00 |
| 0.7 | 77:06 | 80:03 | 87:05 | 120:00 |
| 0.8 | 77:08 | 80:06 | 87:06 | 120:00 |
| 0.9 | 77:09 | 80:06 | 87:09 | 120:00 |
| 1.0 | 77:09 | 80:08 | 87:11 | 120:00 |
| 1.1 | 78:00 | 80:09 | 88:00 | 120:00 |
| 1.2 | 78:00 | 80:11 | 88:03 | 120:00 |
| 1.3 | 78:03 | 81:00 | 88:05 | 120:00 |
| 1.4 | 78:03 | 81:02 | 88:06 | 120:00 |
| 1.5 | 78:06 | 81:03 | 88:09 | 120:00 |
| 1.6 | 78:06 | 81:05 | 89:00 | 120:00 |
| 1.7 | 78:09 | 81:06 | 89:02 | 120:00 |
| 1.8 | 78:09 | 81:08 | 89:05 | 120:00 |
| 1.9 | 79:00 | 81:09 | 89:06 | 120:00 |
| 2.0 | 79:02 | 81:11 | 89:09 | 120:00 |
| 2.1 | 79:03 | 82:00 | 90:00 | 120:00 |
| 2.2 | 79:05 | 82:03 | 90:03 | 120:00 |
| 2.3 | 79:06 | 82:03 | 90:06 | 120:00 |
| 2.4 | 79:09 | 82:06 | 90:09 | 120:00 |
| 2.5 | 79:11 | 82:08 | 91:00 | 120:00 |
| 2.6 | 80:00 | 82:09 | 91:03 | 120:00 |
| 2.7 | 80:03 | 83:00 | 91:06 | 120:00 |
| 2.8 | 80:05 | 83:02 | 91:09 | 120:00 |
| 2.9 | 80:06 | 83:03 | 92:02 | 120:00 |
| 3.0 | 80:09 | 83:06 | 92:06 | 120:00 |
| 3.1 | 80:11 | 83:08 | 92:09 | 120:00 |
| 3.2 | 81:00 | 83:11 | 93:00 | 120:00 |
| 3.3 | 81:03 | 84:00 | 93:06 | 120:00 |
| 3.4 | 81:06 | 84:03 | 93:09 | 120:00 |
| 3.5 | 81:09 | 84:06 | 94:02 | 120:00 |
| 3.6 | 81:11 | 84:08 | 94:06 | 120:00 |
| 3.7 | 82:02 | 84:11 | 95:00 | 120:00 |
| 3.8 | 82:05 | 85:02 | 95:05 | 120:00 |
| 3.9 | 82:06 | 85:03 | 95:11 | 120:00 |
| 4.0 | 82:09 | 85:06 | 96:03 | 120:00 |
| 4.1 | 83:00 | 85:09 | 96:09 | 120:00 |
| 4.2 | 83:05 | 86:00 | 97:05 | 120:00 |
| 4.3 | 83:08 | 86:05 | 98:00 | 120:00 |
| 4.4 | 83:11 | 86:08 | 98:06 | 120:00 |
| 4.5 | 84:03 | 86:11 | 99:02 | 120:00 |
| 4.6 | 84:06 | 87:03 | 99:11 | 120:00 |
| 4.7 | 84:09 | 87:06 | 100:06 | 120:00 |
| 4.8 | 85:02 | 87:11 | 101:05 | 120:00 |
| 4.9 | 85:06 | 88:03 | 102:03 | 120:00 |
| 5.0 | 85:09 | 88:06 | 103:03 | 120:00 |
| 5.1 | 86:03 | 89:00 | 104:03 | 120:00 |
| 5.2 | 86:08 | 89:03 | 105:05 | 120:00 |
| 5.3 | 87:00 | 89:09 | 106:08 | 120:00 |
| 5.4 | 87:06 | 90:03 | 108:00 | 120:00 |
| 5.5 | 88:00 | 90:08 | 109:08 | 120:00 |
| 5.6 | 88:05 | 91:02 | 111:06 | 120:00 |
| 5.7 | 89:00 | 91:08 | 113:09 | 120:00 |
| 5.8 | 89:06 | 92:03 | 116:06 | 120:00 |
| 5.9 | 90:02 | 92:09 | 120:00 | 120:00 |
| 6.0 | 90:09 | 93:06 | 120:00 | 120:00 |
| 6.1 | 91:05 | 94:02 | 120:00 | 120:00 |
| 6.2 | 92:02 | 94:11 | 120:00 | 120:00 |
| 6.3 | 93:00 | 95:08 | 120:00 | 120:00 |
| 6.4 | 93:11 | 96:06 | 120:00 | 120:00 |
| 6.5 | 94:09 | 97:06 | 120:00 | 120:00 |
| 6.6 | 95:11 | 98:08 | 120:00 | 120:00 |
| 6.7 | 97:02 | 99:09 | 120:00 | 120:00 |
| 6.8 | 98:06 | 101:03 | 120:00 | 120:00 |
| 6.9 | 100:02 | 102:09 | 120:00 | 120:00 |
| 7.0 | 102:00 | 104:09 | 120:00 | 120:00 |
| 7.1 | 104:03 | 107:00 | 120:00 | 120:00 |
| 7.2 | 107:03 | 110:00 | 120:00 | 120:00 |
| 7.3 | 111:00 | 114:00 | 120:00 | 120:00 |
| 7.4 | 117:00 | 120:00 | 120:00 | 120:00 |
| 7.5 | 120:00 | 120:00 | 120:00 | 120:00 |
| 7.6 | 120:00 | 120:00 | 120:00 | 120:00 |
| 7.7 | 120:00 | 120:00 | 120:00 | 120:00 |
| 7.8 | 120:00 | 120:00 | 120:00 | 120:00 |
| 7.9 | 120:00 | 120:00 | 120:00 | 120:00 |
| 8.0 | 120:00 | 120:00 | 120:00 | 120:00 |
Relative probabilities that the MCA falls within specified ranges for men born in 1952, by discount rate
| Discount rate (%) | Probability (in percent) that the MCA is— | |||
|---|---|---|---|---|
| 62:00 | 63:01–66:00 | 66:01–69:11 | 70:00 | |
| 0.0 | 25.25 | 7.81 | 23.48 | 43.46 |
| 0.1 | 25.46 | 7.85 | 23.57 | 43.13 |
| 0.2 | 25.68 | 7.87 | 23.99 | 42.46 |
| 0.3 | 25.90 | 7.89 | 24.42 | 41.79 |
| 0.4 | 26.34 | 7.70 | 24.50 | 41.46 |
| 0.5 | 26.56 | 7.99 | 24.68 | 40.77 |
| 0.6 | 26.78 | 8.02 | 25.11 | 40.09 |
| 0.7 | 27.00 | 8.06 | 25.54 | 39.41 |
| 0.8 | 27.44 | 8.12 | 25.71 | 38.72 |
| 0.9 | 27.66 | 8.16 | 26.14 | 38.04 |
| 1.0 | 27.88 | 8.19 | 26.57 | 37.36 |
| 1.1 | 28.33 | 8.25 | 26.75 | 36.67 |
| 1.2 | 28.56 | 8.27 | 27.19 | 35.98 |
| 1.3 | 29.03 | 8.07 | 27.61 | 35.29 |
| 1.4 | 29.26 | 8.37 | 27.76 | 34.60 |
| 1.5 | 29.72 | 8.18 | 28.53 | 33.57 |
| 1.6 | 29.95 | 8.48 | 28.68 | 32.89 |
| 1.7 | 30.42 | 8.28 | 29.09 | 32.21 |
| 1.8 | 30.65 | 8.58 | 29.58 | 31.19 |
| 1.9 | 31.12 | 8.64 | 29.73 | 30.51 |
| 2.0 | 31.61 | 8.42 | 30.48 | 29.48 |
| 2.1 | 31.85 | 8.74 | 30.93 | 28.48 |
| 2.2 | 32.33 | 8.82 | 31.36 | 27.49 |
| 2.3 | 32.82 | 8.61 | 31.74 | 26.82 |
| 2.4 | 33.30 | 8.69 | 32.18 | 25.83 |
| 2.5 | 33.79 | 8.77 | 32.60 | 24.85 |
| 2.6 | 34.30 | 8.82 | 33.30 | 23.58 |
| 2.7 | 34.80 | 8.89 | 33.68 | 22.63 |
| 2.8 | 35.31 | 8.97 | 34.04 | 21.68 |
| 2.9 | 35.82 | 9.05 | 34.65 | 20.48 |
| 3.0 | 36.33 | 9.13 | 35.25 | 19.29 |
| 3.1 | 36.83 | 9.22 | 35.55 | 18.40 |
| 3.2 | 37.37 | 9.57 | 35.80 | 17.27 |
| 3.3 | 38.17 | 9.39 | 36.54 | 15.91 |
| 3.4 | 38.70 | 9.47 | 37.01 | 14.82 |
| 3.5 | 39.50 | 9.60 | 37.08 | 13.82 |
| 3.6 | 40.03 | 9.69 | 37.68 | 12.60 |
| 3.7 | 40.87 | 9.78 | 37.94 | 11.41 |
| 3.8 | 41.71 | 9.91 | 38.03 | 10.35 |
| 3.9 | 42.27 | 9.99 | 38.65 | 9.08 |
| 4.0 | 43.12 | 10.12 | 38.57 | 8.19 |
| 4.1 | 43.99 | 10.22 | 38.67 | 7.12 |
| 4.2 | 45.16 | 10.03 | 38.73 | 6.07 |
| 4.3 | 46.05 | 10.49 | 38.38 | 5.09 |
| 4.4 | 46.93 | 10.61 | 38.18 | 4.28 |
| 4.5 | 48.17 | 10.37 | 37.90 | 3.56 |
| 4.6 | 49.10 | 10.81 | 37.32 | 2.77 |
| 4.7 | 50.34 | 10.94 | 36.49 | 2.23 |
| 4.8 | 51.62 | 11.02 | 35.69 | 1.67 |
| 4.9 | 52.91 | 11.11 | 34.75 | 1.23 |
| 5.0 | 54.21 | 11.19 | 33.77 | 0.84 |
| 5.1 | 55.87 | 11.24 | 32.33 | 0.56 |
| 5.2 | 57.54 | 10.93 | 31.19 | 0.34 |
| 5.3 | 59.23 | 10.95 | 29.63 | 0.19 |
| 5.4 | 60.94 | 11.25 | 27.72 | 0.09 |
| 5.5 | 62.99 | 10.85 | 26.12 | 0.04 |
| 5.6 | 64.71 | 11.08 | 24.20 | 0.01 |
| 5.7 | 67.11 | 10.57 | 22.32 | a |
| 5.8 | 69.15 | 10.66 | 20.18 | a |
| 5.9 | 71.85 | 10.04 | 18.11 | . . . |
| 6.0 | 74.17 | 9.92 | 15.91 | . . . |
| 6.1 | 76.73 | 9.45 | 13.82 | . . . |
| 6.2 | 79.52 | 8.86 | 11.62 | . . . |
| 6.3 | 82.46 | 7.82 | 9.72 | . . . |
| 6.4 | 85.45 | 6.89 | 7.66 | . . . |
| 6.5 | 88.14 | 6.08 | 5.78 | . . . |
| 6.6 | 90.92 | 4.91 | 4.17 | . . . |
| 6.7 | 93.49 | 3.65 | 2.85 | . . . |
| 6.8 | 95.60 | 2.63 | 1.77 | . . . |
| 6.9 | 97.43 | 1.59 | 0.98 | . . . |
| 7.0 | 98.66 | 0.89 | 0.45 | . . . |
| 7.1 | 99.46 | 0.39 | 0.15 | . . . |
| 7.2 | 99.86 | 0.11 | 0.03 | . . . |
| 7.3 | 99.98 | 0.01 | a | |
| 7.4 | 100.00 | a | . . . | . . . |
| 7.5 | 100.00 | . . . | . . . | . . . |
| 7.6 | 100.00 | . . . | . . . | . . . |
| 7.7 | 100.00 | . . . | . . . | . . . |
| 7.8 | 100.00 | . . . | . . . | . . . |
| 7.9 | 100.00 | . . . | . . . | . . . |
| 8.0 | 100.00 | . . . | . . . | . . . |
| NOTE: . . . = not applicable. | ||||
| a. Less than 0.005 percent. | ||||
Relative probabilities that the MCA falls within specified ranges for women born in 1952, by discount rate
| Discount rate (%) | Probability (in percent) that the MCA is— | |||
|---|---|---|---|---|
| 62:00 | 63:01–66:00 | 66:01–69:11 | 70:00 | |
| 0.0 | 18.54 | 6.51 | 21.13 | 53.82 |
| 0.1 | 18.71 | 6.54 | 21.26 | 53.49 |
| 0.2 | 18.89 | 6.56 | 21.70 | 52.84 |
| 0.3 | 19.07 | 6.59 | 22.15 | 52.19 |
| 0.4 | 19.44 | 6.44 | 22.26 | 51.87 |
| 0.5 | 19.62 | 6.69 | 22.51 | 51.19 |
| 0.6 | 19.80 | 6.72 | 22.97 | 50.50 |
| 0.7 | 19.99 | 6.75 | 23.44 | 49.82 |
| 0.8 | 20.35 | 6.82 | 23.69 | 49.14 |
| 0.9 | 20.53 | 6.85 | 24.16 | 48.46 |
| 1.0 | 20.71 | 6.89 | 24.62 | 47.78 |
| 1.1 | 21.09 | 6.94 | 24.90 | 47.07 |
| 1.2 | 21.28 | 6.96 | 25.39 | 46.37 |
| 1.3 | 21.67 | 6.81 | 25.86 | 45.66 |
| 1.4 | 21.86 | 7.07 | 26.11 | 44.96 |
| 1.5 | 22.25 | 6.92 | 26.94 | 43.90 |
| 1.6 | 22.44 | 7.18 | 27.19 | 43.19 |
| 1.7 | 22.83 | 7.03 | 27.68 | 42.47 |
| 1.8 | 23.02 | 7.29 | 28.30 | 41.39 |
| 1.9 | 23.42 | 7.35 | 28.56 | 40.67 |
| 2.0 | 23.83 | 7.18 | 29.41 | 39.59 |
| 2.1 | 24.03 | 7.47 | 29.99 | 38.51 |
| 2.2 | 24.44 | 7.55 | 30.58 | 37.43 |
| 2.3 | 24.84 | 7.39 | 31.06 | 36.71 |
| 2.4 | 25.25 | 7.47 | 31.65 | 35.62 |
| 2.5 | 25.66 | 7.56 | 32.24 | 34.55 |
| 2.6 | 26.09 | 7.62 | 33.17 | 33.12 |
| 2.7 | 26.52 | 7.70 | 33.73 | 32.05 |
| 2.8 | 26.95 | 7.80 | 34.27 | 30.98 |
| 2.9 | 27.38 | 7.90 | 35.14 | 29.58 |
| 3.0 | 27.82 | 7.99 | 36.00 | 28.19 |
| 3.1 | 28.25 | 8.09 | 36.51 | 27.15 |
| 3.2 | 28.71 | 8.43 | 37.07 | 25.80 |
| 3.3 | 29.40 | 8.31 | 38.15 | 24.14 |
| 3.4 | 29.85 | 8.42 | 38.91 | 22.82 |
| 3.5 | 30.54 | 8.59 | 39.31 | 21.55 |
| 3.6 | 31.00 | 8.70 | 40.30 | 20.00 |
| 3.7 | 31.74 | 8.82 | 40.96 | 18.47 |
| 3.8 | 32.48 | 9.00 | 41.46 | 17.06 |
| 3.9 | 32.97 | 9.12 | 42.55 | 15.36 |
| 4.0 | 33.71 | 9.30 | 42.89 | 14.10 |
| 4.1 | 34.49 | 9.44 | 43.48 | 12.59 |
| 4.2 | 35.54 | 9.34 | 44.08 | 11.04 |
| 4.3 | 36.34 | 9.84 | 44.26 | 9.55 |
| 4.4 | 37.13 | 10.02 | 44.57 | 8.28 |
| 4.5 | 38.28 | 9.86 | 44.77 | 7.10 |
| 4.6 | 39.13 | 10.36 | 44.75 | 5.76 |
| 4.7 | 40.27 | 10.59 | 44.34 | 4.80 |
| 4.8 | 41.48 | 10.75 | 44.03 | 3.75 |
| 4.9 | 42.70 | 10.93 | 43.48 | 2.88 |
| 5.0 | 43.93 | 11.12 | 42.89 | 2.07 |
| 5.1 | 45.53 | 11.28 | 41.73 | 1.45 |
| 5.2 | 47.16 | 11.09 | 40.81 | 0.94 |
| 5.3 | 48.81 | 11.23 | 39.39 | 0.56 |
| 5.4 | 50.52 | 11.69 | 37.49 | 0.29 |
| 5.5 | 52.58 | 11.44 | 35.85 | 0.13 |
| 5.6 | 54.34 | 11.83 | 33.79 | 0.05 |
| 5.7 | 56.81 | 11.49 | 31.68 | 0.01 |
| 5.8 | 58.97 | 11.79 | 29.23 | a |
| 5.9 | 61.85 | 11.34 | 26.81 | . . . |
| 6.0 | 64.38 | 11.48 | 24.14 | . . . |
| 6.1 | 67.24 | 11.21 | 21.55 | . . . |
| 6.2 | 70.42 | 10.82 | 18.76 | . . . |
| 6.3 | 73.87 | 9.92 | 16.21 | . . . |
| 6.4 | 77.51 | 9.14 | 13.35 | . . . |
| 6.5 | 80.93 | 8.47 | 10.60 | . . . |
| 6.6 | 84.64 | 7.26 | 8.09 | . . . |
| 6.7 | 88.31 | 5.78 | 5.91 | . . . |
| 6.8 | 91.54 | 4.52 | 3.94 | . . . |
| 6.9 | 94.60 | 3.03 | 2.37 | . . . |
| 7.0 | 96.89 | 1.90 | 1.20 | . . . |
| 7.1 | 98.59 | 0.95 | 0.46 | . . . |
| 7.2 | 99.57 | 0.32 | 0.11 | . . . |
| 7.3 | 99.94 | 0.05 | 0.01 | |
| 7.4 | 100.00 | a | . . . | . . . |
| 7.5 | 100.00 | . . . | . . . | . . . |
| 7.6 | 100.00 | . . . | . . . | . . . |
| 7.7 | 100.00 | . . . | . . . | . . . |
| 7.8 | 100.00 | . . . | . . . | . . . |
| 7.9 | 100.00 | . . . | . . . | . . . |
| 8.0 | 100.00 | . . . | . . . | . . . |
| NOTE: . . . = not applicable. | ||||
| a. Less than 0.005 percent. | ||||
| Discount rate (%) | Probability (in percent) that the MCA is— | Prospective— | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 62:00 | 63:01–66:00 | 66:01–69:11 | 70:00 | OCA | EOL ($) | |||||||||||
| Age at death | Men | Women | Age at death | Men | Women | Age at death | Men | Women | Age at death | Men | Women | Men | Women | Men | Women | |
| 0.0 | 62:00–76:10 | 25.25 | 18.54 | 76:11–79:08 | 7.81 | 6.51 | 79:09–86:05 | 23.48 | 21.13 | 86:06–120:00 | 43.46 | 53.82 | 69:07 | 70:00 | 12.95 | 9.90 |
| 0.1 | 62:00–76:11 | 25.46 | 18.71 | 77:00–79:09 | 7.85 | 6.54 | 79:10–86:06 | 23.57 | 21.26 | 86:07–120:00 | 43.13 | 53.49 | 69:06 | 70:00 | 12.92 | 9.93 |
| 0.2 | 62:00–77:00 | 25.68 | 18.89 | 77:01–79:10 | 7.87 | 6.56 | 79:11–86:08 | 23.99 | 21.70 | 86:09–120:00 | 42.46 | 52.84 | 69:05 | 70:00 | 12.88 | 9.96 |
| 0.3 | 62:00–77:01 | 25.90 | 19.07 | 77:02–79:11 | 7.89 | 6.59 | 80:00–86:10 | 24.42 | 22.15 | 86:11–120:00 | 41.79 | 52.19 | 69:04 | 70:00 | 12.83 | 9.98 |
| 0.4 | 62:00–77:03 | 26.34 | 19.44 | 77:04–80:00 | 7.70 | 6.44 | 80:01–86:11 | 24.50 | 22.26 | 87:00–120:00 | 41.46 | 51.87 | 69:03 | 70:00 | 12.77 | 10.01 |
| 0.5 | 62:00–77:04 | 26.56 | 19.62 | 77:05–80:02 | 7.99 | 6.69 | 80:03–87:01 | 24.68 | 22.51 | 87:02–120:00 | 40.77 | 51.19 | 69:02 | 70:00 | 12.70 | 10.04 |
| 0.6 | 62:00–77:05 | 26.78 | 19.80 | 77:06–80:03 | 8.02 | 6.72 | 80:04–87:03 | 25.11 | 22.97 | 87:04–120:00 | 40.09 | 50.50 | 69:01 | 70:00 | 12.63 | 10.07 |
| 0.7 | 62:00–77:06 | 27.00 | 19.99 | 77:07–80:04 | 8.06 | 6.75 | 80:05–87:05 | 25.54 | 23.44 | 87:06–120:00 | 39.41 | 49.82 | 68:11 | 70:00 | 12.54 | 10.11 |
| 0.8 | 62:00–77:08 | 27.44 | 20.35 | 77:09–80:06 | 8.12 | 6.82 | 80:07–87:07 | 25.71 | 23.69 | 87:08–120:00 | 38.72 | 49.14 | 68:10 | 69:11 | 12.45 | 10.13 |
| 0.9 | 62:00–77:09 | 27.66 | 20.53 | 77:10–80:07 | 8.16 | 6.85 | 80:08–87:09 | 26.14 | 24.16 | 87:10–120:00 | 38.04 | 48.46 | 68:09 | 69:10 | 12.36 | 10.15 |
| 1.0 | 62:00–77:10 | 27.88 | 20.71 | 77:11–80:08 | 8.19 | 6.89 | 80:09–87:11 | 26.57 | 24.62 | 88:00–120:00 | 37.36 | 47.78 | 68:08 | 69:08 | 12.26 | 10.15 |
| 1.1 | 62:00–78:00 | 28.33 | 21.09 | 78:01–80:10 | 8.25 | 6.94 | 80:11–88:01 | 26.75 | 24.90 | 88:02–120:00 | 36.67 | 47.07 | 68:07 | 69:07 | 12.15 | 10.14 |
| 1.2 | 62:00–78:01 | 28.56 | 21.28 | 78:02–80:11 | 8.27 | 6.96 | 81:00–88:03 | 27.19 | 25.39 | 88:04–120:00 | 35.98 | 46.37 | 68:06 | 69:06 | 12.04 | 10.12 |
| 1.3 | 62:00–78:03 | 29.03 | 21.67 | 78:04–81:00 | 8.07 | 6.81 | 81:01–88:05 | 27.61 | 25.86 | 88:06–120:00 | 35.29 | 45.66 | 68:05 | 69:05 | 11.92 | 10.09 |
| 1.4 | 62:00–78:04 | 29.26 | 21.86 | 78:05–81:02 | 8.37 | 7.07 | 81:03–88:07 | 27.76 | 26.11 | 88:08–120:00 | 34.60 | 44.96 | 68:04 | 69:03 | 11.80 | 10.05 |
| 1.5 | 62:00–78:06 | 29.72 | 22.25 | 78:07–81:03 | 8.18 | 6.92 | 81:04–88:10 | 28.53 | 26.94 | 88:11–120:00 | 33.57 | 43.90 | 68:03 | 69:02 | 11.68 | 10.00 |
| 1.6 | 62:00–78:07 | 29.95 | 22.44 | 78:08–81:05 | 8.48 | 7.18 | 81:06–89:00 | 28.68 | 27.19 | 89:01–120:00 | 32.89 | 43.19 | 68:01 | 69:01 | 11.55 | 9.94 |
| 1.7 | 62:00–78:09 | 30.42 | 22.83 | 78:10–81:06 | 8.28 | 7.03 | 81:07–89:02 | 29.09 | 27.68 | 89:03–120:00 | 32.21 | 42.47 | 68:00 | 69:00 | 11.42 | 9.87 |
| 1.8 | 62:00–78:10 | 30.65 | 23.02 | 78:11–81:08 | 8.58 | 7.29 | 81:09–89:05 | 29.58 | 28.30 | 89:06–120:00 | 31.19 | 41.39 | 67:11 | 68:11 | 11.28 | 9.80 |
| 1.9 | 62:00–79:00 | 31.12 | 23.42 | 79:01–81:10 | 8.64 | 7.35 | 81:11–89:07 | 29.73 | 28.56 | 89:08–120:00 | 30.51 | 40.67 | 67:10 | 68:09 | 11.15 | 9.72 |
| 2.0 | 62:00–79:02 | 31.61 | 23.83 | 79:03–81:11 | 8.42 | 7.18 | 82:00–89:10 | 30.48 | 29.41 | 89:11–120:00 | 29.48 | 39.59 | 67:09 | 68:08 | 11.01 | 9.64 |
| 2.1 | 62:00–79:03 | 31.85 | 24.03 | 79:04–82:01 | 8.74 | 7.47 | 82:02–90:01 | 30.93 | 29.99 | 90:02–120:00 | 28.48 | 38.51 | 67:08 | 68:07 | 10.87 | 9.55 |
| 2.2 | 62:00–79:05 | 32.33 | 24.44 | 79:06–82:03 | 8.82 | 7.55 | 82:04–90:04 | 31.36 | 30.58 | 90:05–120:00 | 27.49 | 37.43 | 67:07 | 68:06 | 10.72 | 9.45 |
| 2.3 | 62:00–79:07 | 32.82 | 24.84 | 79:08–82:04 | 8.61 | 7.39 | 82:05–90:06 | 31.74 | 31.06 | 90:07–120:00 | 26.82 | 36.71 | 67:06 | 68:05 | 10.58 | 9.35 |
| 2.4 | 62:00–79:09 | 33.30 | 25.25 | 79:10–82:06 | 8.69 | 7.47 | 82:07–90:09 | 32.18 | 31.65 | 90:10–120:00 | 25.83 | 35.62 | 67:05 | 68:03 | 10.44 | 9.25 |
| 2.5 | 62:00–79:11 | 33.79 | 25.66 | 80:00–82:08 | 8.77 | 7.56 | 82:09–91:00 | 32.60 | 32.24 | 91:01–120:00 | 24.85 | 34.55 | 67:04 | 68:02 | 10.29 | 9.14 |
| 2.6 | 62:00–80:01 | 34.30 | 26.09 | 80:02–82:10 | 8.82 | 7.62 | 82:11–91:04 | 33.30 | 33.17 | 91:05–120:00 | 23.58 | 33.12 | 67:02 | 68:01 | 10.15 | 9.03 |
| 2.7 | 62:00–80:03 | 34.80 | 26.52 | 80:04–83:00 | 8.89 | 7.70 | 83:01–91:07 | 33.68 | 33.73 | 91:08–120:00 | 22.63 | 32.05 | 67:01 | 68:00 | 10.00 | 8.91 |
| 2.8 | 62:00–80:05 | 35.31 | 26.95 | 80:06–83:02 | 8.97 | 7.80 | 83:03–91:10 | 34.04 | 34.27 | 91:11–120:00 | 21.68 | 30.98 | 67:00 | 67:11 | 9.86 | 8.80 |
| 2.9 | 62:00–80:07 | 35.82 | 27.38 | 80:08–83:04 | 9.05 | 7.90 | 83:05–92:02 | 34.65 | 35.14 | 92:03–120:00 | 20.48 | 29.58 | 66:11 | 67:10 | 9.71 | 8.68 |
| 3.0 | 62:00–80:09 | 36.33 | 27.82 | 80:10–83:06 | 9.13 | 7.99 | 83:07–92:06 | 35.25 | 36.00 | 92:07–120:00 | 19.29 | 28.19 | 65:01 | 67:08 | 9.56 | 8.56 |
| 3.1 | 62:00–80:11 | 36.83 | 28.25 | 81:00–83:08 | 9.22 | 8.09 | 83:09–92:09 | 35.55 | 36.51 | 92:10–120:00 | 18.40 | 27.15 | 65:00 | 67:07 | 9.24 | 8.43 |
| 3.2 | 62:00–81:01 | 37.37 | 28.71 | 81:02–83:11 | 9.57 | 8.43 | 84:00–93:01 | 35.80 | 37.07 | 93:02–120:00 | 17.27 | 25.80 | 64:10 | 67:06 | 8.93 | 8.31 |
| 3.3 | 62:00–81:04 | 38.17 | 29.40 | 81:05–84:01 | 9.39 | 8.31 | 84:02–93:06 | 36.54 | 38.15 | 93:07–120:00 | 15.91 | 24.14 | 64:09 | 67:05 | 8.63 | 8.19 |
| 3.4 | 62:00–81:06 | 38.70 | 29.85 | 81:07–84:03 | 9.47 | 8.42 | 84:04–93:10 | 37.01 | 38.91 | 93:11–120:00 | 14.82 | 22.82 | 64:08 | 67:04 | 8.33 | 8.07 |
| 3.5 | 62:00–81:09 | 39.50 | 30.54 | 81:10–84:06 | 9.60 | 8.59 | 84:07–94:02 | 37.08 | 39.31 | 94:03–120:00 | 13.82 | 21.55 | 64:07 | 67:03 | 8.04 | 7.94 |
| 3.6 | 62:00–81:11 | 40.03 | 31.00 | 82:00–84:08 | 9.69 | 8.70 | 84:09–94:07 | 37.68 | 40.30 | 94:08–120:00 | 12.60 | 20.00 | 64:06 | 67:02 | 7.75 | 7.82 |
| 3.7 | 62:00–82:02 | 40.87 | 31.74 | 82:03–84:11 | 9.78 | 8.82 | 85:00–95:00 | 37.94 | 40.96 | 95:01–120:00 | 11.41 | 18.47 | 64:05 | 67:00 | 7.46 | 7.70 |
| 3.8 | 62:00–82:05 | 41.71 | 32.48 | 82:06–85:02 | 9.91 | 9.00 | 85:03–95:05 | 38.03 | 41.46 | 95:06–120:00 | 10.35 | 17.06 | 62:00 | 66:11 | 7.07 | 7.58 |
| 3.9 | 62:00–82:07 | 42.27 | 32.97 | 82:08–85:04 | 9.99 | 9.12 | 85:05–95:11 | 38.65 | 42.55 | 96:00–120:00 | 9.08 | 15.36 | 62:00 | 65:00 | 6.60 | 7.40 |
| 4.0 | 62:00–82:10 | 43.12 | 33.71 | 82:11–85:07 | 10.12 | 9.30 | 85:08–96:04 | 38.57 | 42.89 | 96:05–120:00 | 8.19 | 14.10 | 62:00 | 64:11 | 6.15 | 7.11 |
| 4.1 | 62:00–83:01 | 43.99 | 34.49 | 83:02–85:10 | 10.22 | 9.44 | 85:11–96:10 | 38.67 | 43.48 | 96:11–120:00 | 7.12 | 12.59 | 62:00 | 64:10 | 5.71 | 6.83 |
| 4.2 | 62:00–83:05 | 45.16 | 35.54 | 83:06–86:01 | 10.03 | 9.34 | 86:02–97:05 | 38.73 | 44.08 | 97:06–120:00 | 6.07 | 11.04 | 62:00 | 64:08 | 5.29 | 6.55 |
| 4.3 | 62:00–83:08 | 46.05 | 36.34 | 83:09–86:05 | 10.49 | 9.84 | 86:06–98:00 | 38.38 | 44.26 | 98:01–120:00 | 5.09 | 9.55 | 62:00 | 64:07 | 4.89 | 6.27 |
| 4.4 | 62:00–83:11 | 46.93 | 37.13 | 84:00–86:08 | 10.61 | 10.02 | 86:09–98:07 | 38.18 | 44.57 | 98:08–120:00 | 4.28 | 8.28 | 62:00 | 64:06 | 4.50 | 6.01 |
| 4.5 | 62:00–84:03 | 48.17 | 38.28 | 84:04–86:11 | 10.37 | 9.86 | 87:00–99:02 | 37.90 | 44.77 | 99:03–120:00 | 3.56 | 7.10 | 62:00 | 64:05 | 4.13 | 5.75 |
| 4.6 | 62:00–84:06 | 49.10 | 39.13 | 84:07–87:03 | 10.81 | 10.36 | 87:04–99:11 | 37.32 | 44.75 | 100:00–120:00 | 2.77 | 5.76 | 62:00 | 62:00 | 3.78 | 5.32 |
| 4.7 | 62:00–84:10 | 50.34 | 40.27 | 84:11–87:07 | 10.94 | 10.59 | 87:08–100:07 | 36.49 | 44.34 | 100:08–120:00 | 2.23 | 4.80 | 62:00 | 62:00 | 3.44 | 4.88 |
| 4.8 | 62:00–85:02 | 51.62 | 41.48 | 85:03–87:11 | 11.02 | 10.75 | 88:00–101:05 | 35.69 | 44.03 | 101:06–120:00 | 1.67 | 3.75 | 62:00 | 62:00 | 3.12 | 4.45 |
| 4.9 | 62:00–85:06 | 52.91 | 42.70 | 85:07–88:03 | 11.11 | 10.93 | 88:04–102:03 | 34.75 | 43.48 | 102:04–120:00 | 1.23 | 2.88 | 62:00 | 62:00 | 2.82 | 4.05 |
| 5.0 | 62:00–85:10 | 54.21 | 43.93 | 85:11–88:07 | 11.19 | 11.12 | 88:08–103:03 | 33.77 | 42.89 | 103:04–120:00 | 0.84 | 2.07 | 62:00 | 62:00 | 2.53 | 3.66 |
| 5.1 | 62:00–86:03 | 55.87 | 45.53 | 86:04–89:00 | 11.24 | 11.28 | 89:01–104:03 | 32.33 | 41.73 | 104:04–120:00 | 0.56 | 1.45 | 62:00 | 62:00 | 2.26 | 3.30 |
| 5.2 | 62:00–86:08 | 57.54 | 47.16 | 86:09–89:04 | 10.93 | 11.09 | 89:05–105:05 | 31.19 | 40.81 | 105:06–120:00 | 0.34 | 0.94 | 62:00 | 62:00 | 2.01 | 2.95 |
| 5.3 | 62:00–87:01 | 59.23 | 48.81 | 87:02–89:09 | 10.95 | 11.23 | 89:10–106:08 | 29.63 | 39.39 | 106:09–120:00 | 0.19 | 0.56 | 62:00 | 62:00 | 1.77 | 2.63 |
| 5.4 | 62:00–87:06 | 60.94 | 50.52 | 87:07–90:03 | 11.25 | 11.69 | 90:04–108:01 | 27.72 | 37.49 | 108:02–120:00 | 0.09 | 0.29 | 62:00 | 62:00 | 1.55 | 2.32 |
| 5.5 | 62:00–88:00 | 62.99 | 52.58 | 88:01–90:08 | 10.85 | 11.44 | 90:09–109:08 | 26.12 | 35.85 | 109:09–120:00 | 0.04 | 0.13 | 62:00 | 62:00 | 1.34 | 2.03 |
| 5.6 | 62:00–88:05 | 64.71 | 54.34 | 88:06–91:02 | 11.08 | 11.83 | 91:03–111:07 | 24.20 | 33.79 | 111:08–120:00 | 0.01 | 0.05 | 62:00 | 62:00 | 1.15 | 1.77 |
| 5.7 | 62:00–89:00 | 67.11 | 56.81 | 89:01–91:08 | 10.57 | 11.49 | 91:09–113:10 | 22.32 | 31.68 | 113:11–120:00 | a | 0.01 | 62:00 | 62:00 | 0.97 | 1.52 |
| 5.8 | 62:00–89:06 | 69.15 | 58.97 | 89:07–92:03 | 10.66 | 11.79 | 92:04–116:07 | 20.18 | 29.23 | 116:08–120:00 | a | a | 62:00 | 62:00 | 0.81 | 1.29 |
| 5.9 | 62:00–90:02 | 71.85 | 61.85 | 90:03–92:10 | 10.04 | 11.34 | 92:11–120:00 | 18.11 | 26.81 | . . . | . . . | . . . | 62:00 | 62:00 | 0.67 | 1.08 |
| 6.0 | 62:00–90:09 | 74.17 | 64.38 | 90:10–93:06 | 9.92 | 11.48 | 93:07–120:00 | 15.91 | 24.14 | . . . | . . . | . . . | 62:00 | 62:00 | 0.54 | 0.89 |
| 6.1 | 62:00–91:05 | 76.73 | 67.24 | 91:06–94:02 | 9.45 | 11.21 | 94:03–120:00 | 13.82 | 21.55 | . . . | . . . | . . . | 62:00 | 62:00 | 0.43 | 0.72 |
| 6.2 | 62:00–92:02 | 79.52 | 70.42 | 92:03–94:11 | 8.86 | 10.82 | 95:00–120:00 | 11.62 | 18.76 | . . . | . . . | . . . | 62:00 | 62:00 | 0.33 | 0.57 |
| 6.3 | 62:00–93:00 | 82.46 | 73.87 | 93:01–95:08 | 7.82 | 9.92 | 95:09–120:00 | 9.72 | 16.21 | . . . | . . . | . . . | 62:00 | 62:00 | 0.24 | 0.44 |
| 6.4 | 62:00–93:11 | 85.45 | 77.51 | 94:00–96:07 | 6.89 | 9.14 | 96:08–120:00 | 7.66 | 13.35 | . . . | . . . | . . . | 62:00 | 62:00 | 0.18 | 0.32 |
| 6.5 | 62:00–94:10 | 88.14 | 80.93 | 94:11–97:07 | 6.08 | 8.47 | 97:08–120:00 | 5.78 | 10.60 | . . . | . . . | . . . | 62:00 | 62:00 | 0.12 | 0.23 |
| 6.6 | 62:00–95:11 | 90.92 | 84.64 | 96:00–98:08 | 4.91 | 7.26 | 98:09–120:00 | 4.17 | 8.09 | . . . | . . . | . . . | 62:00 | 62:00 | 0.08 | 0.16 |
| 6.7 | 62:00–97:02 | 93.49 | 88.31 | 97:03–99:10 | 3.65 | 5.78 | 99:11–120:00 | 2.85 | 5.91 | . . . | . . . | . . . | 62:00 | 62:00 | 0.05 | 0.10 |
| 6.8 | 62:00–98:06 | 95.60 | 91.54 | 98:07–101:03 | 2.63 | 4.52 | 101:04–120:00 | 1.77 | 3.94 | . . . | . . . | . . . | 62:00 | 62:00 | 0.02 | 0.06 |
| 6.9 | 62:00–100:02 | 97.43 | 94.60 | 100:03–102:10 | 1.59 | 3.03 | 102:11–120:00 | 0.98 | 2.37 | . . . | . . . | . . . | 62:00 | 62:00 | 0.01 | 0.03 |
| 7.0 | 62:00–102:00 | 98.66 | 96.89 | 102:01–104:09 | 0.89 | 1.90 | 104:10–120:00 | 0.45 | 1.20 | . . . | . . . | . . . | 62:00 | 62:00 | b | 0.01 |
| 7.1 | 62:00–104:04 | 99.46 | 98.59 | 104:05–107:01 | 0.39 | 0.95 | 107:02–120:00 | 0.15 | 0.46 | . . . | . . . | . . . | 62:00 | 62:00 | b | b |
| 7.2 | 62:00–107:03 | 99.86 | 99.57 | 107:04–110:00 | 0.11 | 0.32 | 110:01–120:00 | 0.03 | 0.11 | . . . | . . . | . . . | 62:00 | 62:00 | b | b |
| 7.3 | 62:00–111:01 | 99.98 | 99.94 | 111:02–114:00 | 0.01 | 0.05 | 114:01–120:00 | a | 0.01 | 62:00 | 62:00 | b | b | |||
| 7.4 | 62:00–117:00 | 100.00 | 100.00 | 117:01–120:00 | a | a | . . . | . . . | . . . | . . . | . . . | . . . | 62:00 | 62:00 | b | b |
| 7.5 | 62:00–120:00 | 100.00 | 100.00 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 62:00 | 62:00 | 0.00 | 0.00 |
| 7.6 | 62:00–120:00 | 100.00 | 100.00 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 62:00 | 62:00 | 0.00 | 0.00 |
| 7.7 | 62:00–120:00 | 100.00 | 100.00 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 62:00 | 62:00 | 0.00 | 0.00 |
| 7.8 | 62:00–120:00 | 100.00 | 100.00 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 62:00 | 62:00 | 0.00 | 0.00 |
| 7.9 | 62:00–120:00 | 100.00 | 100.00 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 62:00 | 62:00 | 0.00 | 0.00 |
| 8.0 | 62:00–120:00 | 100.00 | 100.00 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 62:00 | 62:00 | 0.00 | 0.00 |
| SOURCE: Author's calculations. | ||||||||||||||||
| NOTES: Claiming ages from 62:01 through 63:00 do not maximize lifetime benefits for individuals of the 1952 birth cohort, regardless of age at death or discount rate.
Rounded components of percentage distributions (the sum of the columns for men or the sum of the columns for women at a given discount rate) do not necessarily sum to 100.00.
. . . = not applicable.
|
||||||||||||||||
| a. Less than 0.005 percent. | ||||||||||||||||
| b. Less than $0.005. | ||||||||||||||||
Clearly, higher discount rates favor lower MCAs. In Charts 1–3, 70:00 is the dominant MCA category at 0.0 percent, but it gradually gives way to younger MCAs as rates progress across the lower range that signifies heavy cash and bond asset allocations. In the middle range, near the balanced-allocation rate of 4.6 percent, the probability that 62:00 is the MCA starts to increase rapidly, and comes to dominate the other MCA categories as rates climb into the stock-heavy range. An MCA of 70:00 ceases to exist altogether at discount rates above 5.8 percent. A notable feature of these plots is the increasing sensitivity to rate. Generally, at discount rates lower than that of the balanced allocation, the slopes are more gradual and are thus less sensitive to discount rate changes than are those at rates higher than the balanced allocation. In those latter regions, the slopes—particularly for 62:00—are steeper and therefore more sensitive to the increasing rate. Also of note is that no claiming age in the second MCA category, from 62:01 to the first bend point at 63:00, is ever maximizing for any death age at any discount rate,5 and claiming ages in the category from 63:01 to the FRA are rarely maximizing.
Perhaps the most salient feature of these MCA plots for the 1952 cohort is that with a 7.5 percent or higher real rate of return, no claiming age can ever produce more lifetime benefit than 62:00, even if the participant lives to age 120. Therefore, a consideration of alternative claiming ages, at least for this cohort, is limited to discount rates of less than 7.5 percent. Although one could argue that discounting potential benefits at a real rate of 7.5 percent is somewhat reckless, it is certainly not unrealistic. If one intends to service debt with the benefit stream, various long-term obligations such as home equity loans or credit cards financed at 7.5 percent or more are not uncommon. If one intends to invest the benefit stream, the historical annual average real return on small-company stocks is substantially higher, though hardly guaranteed to continue, at 8.8 percent (Ibbotson Associates 2011, 54). In any case, it is not the retrospective MCA but the prospective EOL-minimizing OCA that is central to the claiming decision because the age of death is unknown. In that light, even much lower discount rates can strongly favor early claiming.
Prospective OCA and EOL
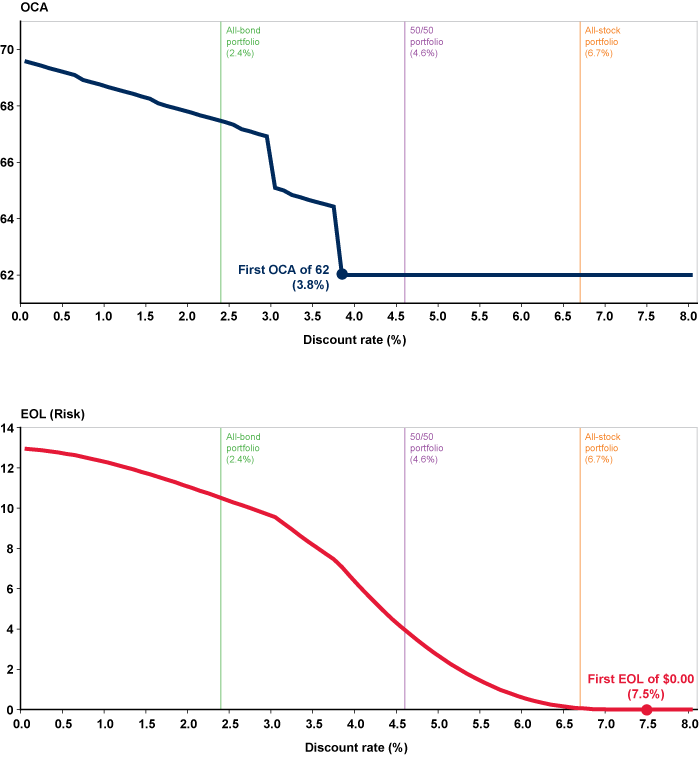
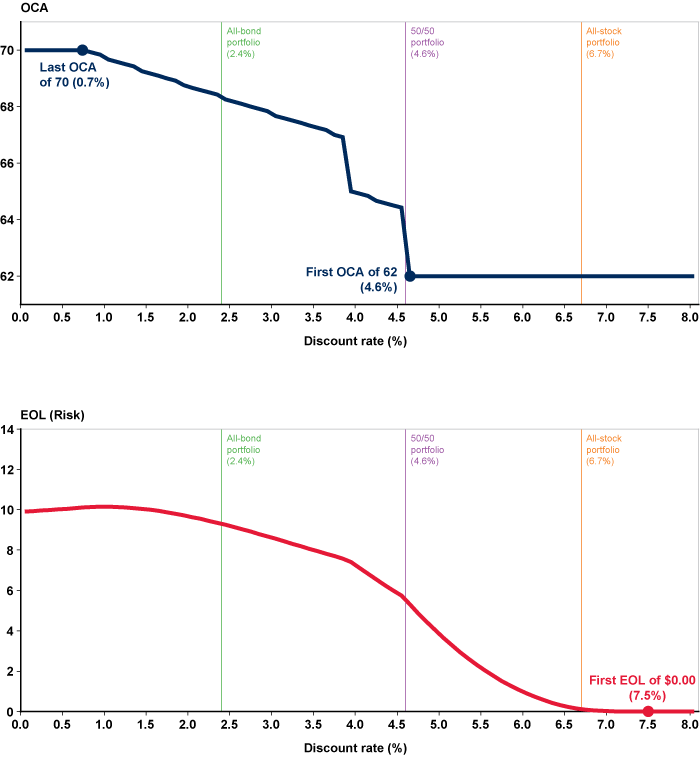
Charts 4 and 5 show, for men and women respectively, the OCA and its associated EOL across the discount-rate spectrum. The lower rates indicate the oldest OCAs,6 as expected; however, they also indicate the highest EOLs. This result reflects the wider distribution of likely MCAs at lower rates (as shown in Charts 2 and 3), making the OCA decision risky at rates within this range. Also notable is that 70:00 is never the OCA for men and is the OCA for women only at rates of 0.7 percent or lower. Both the OCA and EOL decrease as the discount rate increases (with the exception of a slight uptick in EOL for women between 0.0 percent and 1.0 percent).7 Yet as rates increase from 2.9 percent to 3.8 percent for men and from 3.8 percent to 4.6 percent for women, the OCA and the EOL both descend rapidly, indicating high sensitivity to the specific rate. Individuals contemplating discount rates in these narrow ranges should take extra care with rate specification, as the OCA drops from 66:11 to 62:00 with a change of less than 100 basis points for both sexes. For example, using a 2.9 percent discount rate yields an OCA of 66:11 for men born in 1952 (Alleva 2015). Yet as the current analysis suggests, that OCA is surprisingly sensitive to the chosen discount rate. At 2.8 percent, 10 basis points lower, the OCA is virtually the same at 67:00; but at 3.0 percent, only 10 basis points higher, it is 65:01, almost 2 years younger.
OCA and EOL for men born in 1952, by discount rate
| Discount rate (%) | Prospective— | |
|---|---|---|
| OCA | EOL ($) | |
| 0.0 | 69:07 | 12.95 |
| 0.1 | 69:06 | 12.92 |
| 0.2 | 69:05 | 12.88 |
| 0.3 | 69:04 | 12.83 |
| 0.4 | 69:03 | 12.77 |
| 0.5 | 69:02 | 12.70 |
| 0.6 | 69:01 | 12.63 |
| 0.7 | 68:11 | 12.54 |
| 0.8 | 68:10 | 12.45 |
| 0.9 | 68:09 | 12.36 |
| 1.0 | 68:08 | 12.26 |
| 1.1 | 68:07 | 12.15 |
| 1.2 | 68:06 | 12.04 |
| 1.3 | 68:05 | 11.92 |
| 1.4 | 68:04 | 11.80 |
| 1.5 | 68:03 | 11.68 |
| 1.6 | 68:01 | 11.55 |
| 1.7 | 68:00 | 11.42 |
| 1.8 | 67:11 | 11.28 |
| 1.9 | 67:10 | 11.15 |
| 2.0 | 67:09 | 11.01 |
| 2.1 | 67:08 | 10.87 |
| 2.2 | 67:07 | 10.72 |
| 2.3 | 67:06 | 10.58 |
| 2.4 | 67:05 | 10.44 |
| 2.5 | 67:04 | 10.29 |
| 2.6 | 67:02 | 10.15 |
| 2.7 | 67:01 | 10.00 |
| 2.8 | 67:00 | 9.86 |
| 2.9 | 66:11 | 9.71 |
| 3.0 | 65:01 | 9.56 |
| 3.1 | 65:00 | 9.24 |
| 3.2 | 64:10 | 8.93 |
| 3.3 | 64:09 | 8.63 |
| 3.4 | 64:08 | 8.33 |
| 3.5 | 64:07 | 8.04 |
| 3.6 | 64:06 | 7.75 |
| 3.7 | 64:05 | 7.46 |
| 3.8 | 62:00 | 7.07 |
| 3.9 | 62:00 | 6.60 |
| 4.0 | 62:00 | 6.15 |
| 4.1 | 62:00 | 5.71 |
| 4.2 | 62:00 | 5.29 |
| 4.3 | 62:00 | 4.89 |
| 4.4 | 62:00 | 4.50 |
| 4.5 | 62:00 | 4.13 |
| 4.6 | 62:00 | 3.78 |
| 4.7 | 62:00 | 3.44 |
| 4.8 | 62:00 | 3.12 |
| 4.9 | 62:00 | 2.82 |
| 5.0 | 62:00 | 2.53 |
| 5.1 | 62:00 | 2.26 |
| 5.2 | 62:00 | 2.01 |
| 5.3 | 62:00 | 1.77 |
| 5.4 | 62:00 | 1.55 |
| 5.5 | 62:00 | 1.34 |
| 5.6 | 62:00 | 1.15 |
| 5.7 | 62:00 | 0.97 |
| 5.8 | 62:00 | 0.81 |
| 5.9 | 62:00 | 0.67 |
| 6.0 | 62:00 | 0.54 |
| 6.1 | 62:00 | 0.43 |
| 6.2 | 62:00 | 0.33 |
| 6.3 | 62:00 | 0.24 |
| 6.4 | 62:00 | 0.18 |
| 6.5 | 62:00 | 0.12 |
| 6.6 | 62:00 | 0.08 |
| 6.7 | 62:00 | 0.05 |
| 6.8 | 62:00 | 0.02 |
| 6.9 | 62:00 | 0.01 |
| 7.0 | 62:00 | a |
| 7.1 | 62:00 | a |
| 7.2 | 62:00 | a |
| 7.3 | 62:00 | a |
| 7.4 | 62:00 | a |
| 7.5 | 62:00 | 0.00 |
| 7.6 | 62:00 | 0.00 |
| 7.7 | 62:00 | 0.00 |
| 7.8 | 62:00 | 0.00 |
| 7.9 | 62:00 | 0.00 |
| 8.0 | 62:00 | 0.00 |
| a. Less than $0.005. | ||
OCA and EOL for women born in 1952, by discount rate
| Discount rate (%) | Prospective— | |
|---|---|---|
| OCA | EOL ($) | |
| 0.0 | 70:00 | 9.90 |
| 0.1 | 70:00 | 9.93 |
| 0.2 | 70:00 | 9.96 |
| 0.3 | 70:00 | 9.98 |
| 0.4 | 70:00 | 10.01 |
| 0.5 | 70:00 | 10.04 |
| 0.6 | 70:00 | 10.07 |
| 0.7 | 70:00 | 10.11 |
| 0.8 | 69:11 | 10.13 |
| 0.9 | 69:10 | 10.15 |
| 1.0 | 69:08 | 10.15 |
| 1.1 | 69:07 | 10.14 |
| 1.2 | 69:06 | 10.12 |
| 1.3 | 69:05 | 10.09 |
| 1.4 | 69:03 | 10.05 |
| 1.5 | 69:02 | 10.00 |
| 1.6 | 69:01 | 9.94 |
| 1.7 | 69:00 | 9.87 |
| 1.8 | 68:11 | 9.80 |
| 1.9 | 68:09 | 9.72 |
| 2.0 | 68:08 | 9.64 |
| 2.1 | 68:07 | 9.55 |
| 2.2 | 68:06 | 9.45 |
| 2.3 | 68:05 | 9.35 |
| 2.4 | 68:03 | 9.25 |
| 2.5 | 68:02 | 9.14 |
| 2.6 | 68:01 | 9.03 |
| 2.7 | 68:00 | 8.91 |
| 2.8 | 67:11 | 8.80 |
| 2.9 | 67:10 | 8.68 |
| 3.0 | 67:08 | 8.56 |
| 3.1 | 67:07 | 8.43 |
| 3.2 | 67:06 | 8.31 |
| 3.3 | 67:05 | 8.19 |
| 3.4 | 67:04 | 8.07 |
| 3.5 | 67:03 | 7.94 |
| 3.6 | 67:02 | 7.82 |
| 3.7 | 67:00 | 7.70 |
| 3.8 | 66:11 | 7.58 |
| 3.9 | 65:00 | 7.40 |
| 4.0 | 64:11 | 7.11 |
| 4.1 | 64:10 | 6.83 |
| 4.2 | 64:08 | 6.55 |
| 4.3 | 64:07 | 6.27 |
| 4.4 | 64:06 | 6.01 |
| 4.5 | 64:05 | 5.75 |
| 4.6 | 62:00 | 5.32 |
| 4.7 | 62:00 | 4.88 |
| 4.8 | 62:00 | 4.45 |
| 4.9 | 62:00 | 4.05 |
| 5.0 | 62:00 | 3.66 |
| 5.1 | 62:00 | 3.30 |
| 5.2 | 62:00 | 2.95 |
| 5.3 | 62:00 | 2.63 |
| 5.4 | 62:00 | 2.32 |
| 5.5 | 62:00 | 2.03 |
| 5.6 | 62:00 | 1.77 |
| 5.7 | 62:00 | 1.52 |
| 5.8 | 62:00 | 1.29 |
| 5.9 | 62:00 | 1.08 |
| 6.0 | 62:00 | 0.89 |
| 6.1 | 62:00 | 0.72 |
| 6.2 | 62:00 | 0.57 |
| 6.3 | 62:00 | 0.44 |
| 6.4 | 62:00 | 0.32 |
| 6.5 | 62:00 | 0.23 |
| 6.6 | 62:00 | 0.16 |
| 6.7 | 62:00 | 0.10 |
| 6.8 | 62:00 | 0.06 |
| 6.9 | 62:00 | 0.03 |
| 7.0 | 62:00 | 0.01 |
| 7.1 | 62:00 | a |
| 7.2 | 62:00 | a |
| 7.3 | 62:00 | a |
| 7.4 | 62:00 | a |
| 7.5 | 62:00 | 0.00 |
| 7.6 | 62:00 | 0.00 |
| 7.7 | 62:00 | 0.00 |
| 7.8 | 62:00 | 0.00 |
| 7.9 | 62:00 | 0.00 |
| 8.0 | 62:00 | 0.00 |
| a. Less than $0.005. | ||
Above the discount-rate thresholds at which the OCA reaches 62:00, EOLs continue to fall sharply, indicating increasing likelihoods that the OCA will in fact equal the MCA. At 7.5 percent and higher, the EOL is $0.00, as 62:00 will always be maximizing, not just optimal, for both sexes. The OCA is 62:00 at 3.8 percent and higher for men and 4.6 percent and higher for women (Table 2). This result corroborates the work of Spitzer (2006), who finds that at rates of about 4 percent and higher, delayed claiming is generally not advisable. With the expected capital-market returns summarized in Table 1, 3.8 percent indicates a fairly conservative portfolio of roughly one-third stocks and two-thirds bonds, and 4.6 percent indicates a balanced portfolio. Using stochastic simulations of the investment of Social Security benefits into various stock and bond allocations, Manakyan, Ervin, and Claggett (2014) also find that such allocations strongly favor immediate claiming, even if the beneficiary survives to age 96.
Charts 4 and 5 show that at lower discount rates, the OCA is less likely to equal the MCA, and thus will likely turn out to have been the “wrong” choice. That situation suggests that adjusting one's discount rate upwards is one way to lower decision risk. Basing the claiming decision on an arbitrarily higher rate simply to feel more confident in the outcome would seem to be imprudent. However, this study finds that such a rate need never rise above 3.8 percent for men and 4.6 percent for women.
Implied Discount Rates
In selecting a discount rate for the Social Security claiming decision, one might come to consider the inverse of the decision metric; that is, instead of asking what claiming age is prescribed by a given discount rate, one could ask what discount rate is implied by a given claiming age. If a chosen discount rate measures only the extent to which the participant prefers the benefit payments sooner rather than later, then early claiming itself implies a higher discount rate and delayed claiming implies a lower discount rate. For those who would claim early because they need the money for current expenditures, the discount rate is very high, as they would value immediate receipt of benefits much more than the alternative—say, inadequate food or shelter while awaiting later ages to which survival is uncertain. Higher discount rates and immediate claiming could also imply intent to invest the cash flows at equivalently high expected rates of return for use later in retirement. Either way, early claimers inherently place high value on receiving the cash flow sooner.
Conversely, those who delay claiming do so at least in part because they can afford to, and thus their need for immediate benefit payments is less than that of early claimers, which implies lower discount rates. Delayed claimers could also have a strong anticipation of, and a desire to maximize lifetime benefits for, survival to advanced ages (at the expense of maximizing for an earlier death), which in itself implies less need for immediate payments. Chart 1 confirms that delayed claiming is effective mostly at advanced ages and lower discount rates, as later MCAs give way to earlier MCAs as rates increase (implying as before that earlier claiming is more effective at higher rates, even if maximization at advanced ages is one's goal). Thus it could be inferred that delayed claimers desire to maximize lifetime benefits for advanced ages, which is mostly effective at lower rates. Either way, delayed claimers place less value on receiving the cash flow sooner.
Both of the above situations are congruous with the results of this and previous studies. Early claiming is found to be associated with higher rates, and delayed claiming is associated with lower rates.
Conclusion
Alleva (2015) analyzes the Social Security claiming decision using a fixed real rate of 2.9 percent to discount benefits at the long-term average inflation-adjusted government bond rate. Extending that analysis over a broad range of rates, the present study finds that optimizing the decision with lower rates prescribes later claiming ages but with higher associated risk, whereas optimization with higher rates prescribes earlier claiming ages and lower associated risk.
Several other results of this study are noteworthy. First, for both men and women born in 1952 with a real discount rate of 7.5 percent or higher, claiming at age 62 will always maximize lifetime benefits even if death occurs as late as age 120. For these cohorts, this finding effectively caps the range of rates to consider at 7.5 percent.
Secondly, at discount rates above 5.8 percent, claiming at age 70 will not maximize lifetime benefits for either sex at any death age. More importantly, a delay to age 70 is never the optimal choice for men at any discount rate and is optimal for women only at 0.7 percent or lower.
Finally, claiming at age 62 is optimal at discount rates of 3.8 percent or higher for men and 4.6 percent or higher for women. In other words, based on their respective survival functions, claiming at age 62 generates the highest expected lifetime benefits over the full retirement horizon at those rates or higher. Furthermore, those two rates reflect the expected returns on fairly conservative-to-moderate portfolio allocations of no more than one-half stocks. In addition, claiming at age 62 at those rates carries less risk than that associated with the OCA of 66:11 at 2.9 percent, as determined in Alleva (2015). These results indicate that rates higher than 3.8 percent (for men) and 4.6 percent (for women) need not be considered, even to justify immediate claiming with lowered risk.
Notes
1 Specifically, the Social Security Administration's Office of the Chief Actuary uses a 2.9 percent real interest rate for the Alternative II (intermediate) projections of the Social Security trust funds (Board of Trustees 2013, 105).
2 The survival functions used in this study are derived from cohort life tables prepared by the Social Security Administration's Office of the Chief Actuary for the Alternative II (intermediate) projections of the Social Security trust funds (Board of Trustees 2013, 79). For documentation of those survival functions, see Alleva (2016).
3 For the full computational methodology for calculating the MCA, the OCA, and the EOL, see Alleva (2015).
4 Because Social Security benefits are cost-of-living adjusted, all rates in this article are specified in real terms.
5 Meyer and Reichenstein (2012) find similar results.
6 Shoven and Slavov (2012, Figure 2) find similar results.
7 The EOL for women rises from $9.90 at 0.0 percent to $10.15 at 1.0 percent before declining monotonically as rates increase thereafter. The OCA is 70:00 at 0.0 percent and it begins edging younger at 0.8 percent. As rates increase through these lower ranges, the MCA for women shifts younger more quickly than the OCA does, which increases the EOL. Beyond 0.8 percent, however, the dominant MCA tracks increasingly closer to the OCA (as it does for men), thereby reducing the EOL until it reaches $0.00 at the point where MCA and OCA converge (7.5 percent).
References
Alleva, Brian J. 2015. “Minimizing the Risk of Opportunity Loss in the Social Security Claiming Decision.” Journal of Retirement 3(1): 67–86.
———. 2016. “The Longevity Visualizer: An Analytic Tool for Exploring the Cohort Mortality Data Produced by the Office of the Chief Actuary.” Research and Statistics Note No. 2016-02. https://www.socialsecurity.gov/policy/docs/rsnotes/rsn2016-02.html.
[Board of Trustees] Board of Trustees, Federal Old-Age and Survivors Insurance and Federal Disability Insurance Trust Funds. 2013. 2013 Annual Report of the Board of Trustees of the Federal Old-Age and Survivors Insurance and Federal Disability Insurance Trust Funds. Washington, DC: Government Printing Office. https://www.socialsecurity.gov/OACT/TR/2013/tr2013.pdf.
Coile, Courtney, Peter Diamond, Jonathan Gruber, and Alain Jousten. 2002. “Delays in Claiming Social Security Benefits.” Journal of Public Economics 84(3): 357–385.
Friedman, Joseph, and Herbert E. Phillips. 2008. “Optimizing Social Security Benefit Initiation and Postponement Decisions: A Sequential Approach.” Financial Services Review 17(2): 155–168.
Ibbotson Associates. 2011. Ibbotson SBBI 2011 Classic Yearbook: Market Results for Stocks, Bonds, Bills, and Inflation 1926–2010. Chicago, IL: Morningstar, Inc.
Manakyan, Herman, Danny Ervin, and E. Tylor Claggett. 2014. “Take the Money: Should You Draw Social Security Benefits Early?” Retirement Management Journal 4(1): 45–53.
Meyer, William, and William Reichenstein. 2010. “Social Security: When Should You Start Benefits and How to Minimize Longevity Risk?” Journal of Financial Planning 23(3): 52–63.
———. 2012. “Social Security Claiming Strategies for Singles.” Retirement Management Journal 2(3): 61–66.
Sass, Steven A., Wei Sun, and Anthony Webb. 2013. “Social Security Claiming Decision of Married Men and Widow Poverty.” Economics Letters 119(1): 20–23.
Shoven, John B., and Sita Nataraj Slavov. 2012. “The Decision to Delay Social Security Benefits: Theory and Evidence.” NBER Working Paper No. 17866. Cambridge, MA: National Bureau of Economic Research.
———. 2014a. “Does It Pay to Delay Social Security?” Journal of Pension Economics and Finance 13(2): 121–144.
———. 2014b. “Recent Changes in the Gains from Delaying Social Security.” Journal of Financial Planning 27(3): 32–41.
Spitzer, John J. 2006. “Delaying Social Security Payments: A Bootstrap.” Financial Services Review 15(3): 233–245.
Sun, Wei, and Anthony Webb. 2011. “Valuing the Longevity Insurance Acquired by Delayed Claiming of Social Security.” Journal of Risk and Insurance 78(4): 907–929.