Exits from the Disability Insurance Rolls: Estimates from a Competing-Risks Model
Social Security Bulletin, Vol. 77 No. 3, 2017 (released August 2017)
This article explores the causes of growth in the number of disabled workers on the Social Security Disability Insurance (DI) rolls from 1980 through 2010 by estimating the probability of a DI beneficiary's program exit because of recovery, death, or conversion to retired-worker beneficiary, by sex, age, and disability type. Using Social Security administrative data and a competing-risks model to estimate DI exit probabilities, I find that death is the primary reason for program exits among nearly all beneficiary subgroups during their first 9 years on the rolls. Relative to men, women have lower probabilities of exit because of death; younger women also have lower exit probabilities because of recovery. From the 1980s to the 1990s, the probability of exit because of death declined while the probability of exit because of recovery did not improve. Beneficiaries with certain impairments are noteworthy exceptions to these general outcomes.
Lakshmi Raut is with the Office of Research, Evaluation, and Statistics, Office of Retirement and Disability Policy, Social Security Administration.
Acknowledgments: In preparing this draft, I greatly benefitted from many comments and discussions with Paul Davies, Michael Leonesio, Javier Meseguer, David Pattison, Alexander Strand, and an anonymous reviewer from the Social Security Administration's Office of the Chief Actuary.
Contents of this publication are not copyrighted; any items may be reprinted, but citation of the Social Security Bulletin as the source is requested. The findings and conclusions presented in the Bulletin are those of the author and do not necessarily represent the views of the Social Security Administration.
Introduction
| CWHS | Continuous Work History Sample |
| DI | Disability Insurance |
| FRA | full retirement age |
For the Social Security Disability Insurance (DI) program, the numbers of new enrollments and of beneficiaries on the rolls rose rapidly from 1980 through 2010. Clearly, growth in the DI rolls can result when the number of enrollments increases; but it may also result when beneficiaries stay longer in the program. Possible contributing factors include (1) demographic shifts, such as growing shares of younger and female workers entering the rolls; (2) changes in DI policies and in economic conditions (such as high unemployment) influencing workers to enter the program and stay longer in it; and (3) changing health trends, with certain disabling impairments (such as musculoskeletal impairments and mental disorders) becoming more prevalent among various population subgroups. A beneficiary's stay on the DI rolls also depends on individual characteristics such as the type of disability, age at entitlement, sex, employment opportunities, and past health conditions. Available administrative data do not have information on many of these individual characteristics. In this article, I focus on exit-rate patterns by age and sex, by type of disability, and over time, to examine if workforce shifts toward relatively younger workers, more female workers, or more aging workers prone to certain types of disabilities might explain the observed growth in the DI rolls.
A DI beneficiary exits the program for one of three reasons—death, recovery, or conversion to retirement benefits at full retirement age (FRA). A recovery—leaving the program before death or old-age conversion—can be due either to a worker's return to employment that provides a substantial level of earnings or to a Disability Determination Service finding that a beneficiary is no longer disabled. This article does not distinguish between the two.
The probability of exit because of a given cause depends on the probabilities of exit resulting from the competing causes. For instance, the probability of exiting DI because of recovery within a certain time depends on the likelihood that the person did not exit the program earlier because of either death or conversion. Thus, it is important to estimate the exit probabilities of any specific cause jointly with the exit probabilities of the two competing causes. Otherwise, we will have biased estimates (see, for instance, Pintilie 2006). I use a competing-risks statistical method that estimates the exit probabilities for all three competing risks simultaneously. Using these estimates, I present the emerging patterns of DI program exits by age at entitlement, sex, type of disability, and time on the rolls.
A parametric or semiparametric competing-risks hazard model is more appropriate than a cell-frequency method to estimate exit probabilities for two reasons. First, as cells are divided more finely to enhance granularity, some of them may end up containing zero or very few observations. A semiparametric hazard model can handle the small-sample cell problem because it uses information from all cells to estimate parameters that are common to all cells, while the cell-frequency method generally uses a case-by-case graduation method that combines the nearby cell frequencies. The second reason is that a semiparametric duration model can better handle censored observations, which arise because some individuals in the dataset have not yet exited the program at the time of data collection. The censored observations carry useful information about the exit probabilities, and estimates that discard the censored observations are inefficient.
This article is arranged in eight sections, including this introduction. In the second section, I briefly describe the trend of increasing DI entitlements and the data and methodology used in this analysis. In the third section, I first calculate the cumulative incidence of exit because of death, recovery, or conversion for the whole pool of disabled beneficiaries. Then I distinguish beneficiaries by age at entitlement and sex, focusing on beneficiaries who are younger than the FRA, and are thereby at no risk of exit by conversion; so for them, I examine only the probabilities of exit because of recovery or death. I look at exit probabilities by age at entitlement alone, and then by both age and sex. In the fourth section, I compare the estimates from the competing-risks model with direct estimates based on a cell-frequency method published in a Social Security Administration Actuarial Study (Zayatz 2011), first by age alone and then by age and sex. In the fifth section, I analyze how the exit patterns vary among five broad disability-type categories. In the sixth section, I examine how the exit probabilities for each disability type vary by sex. In the seventh section, I analyze how the exit probabilities for each disability type have shifted over time. The eighth section concludes.
Background, Data, and Methodology
This section discusses the historical context and the analytical framework of the study.
Growth in the DI Rolls
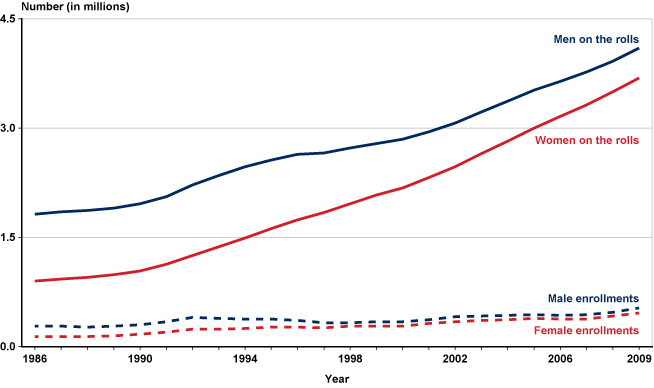
Chart 1 shows the number of male and female disabled-worker beneficiaries on the DI rolls and the number of DI awards to male and female workers during the period 1986–2009. The data are from Zayatz (2011, Tables 3 and 6). All four series increase over time. The number of beneficiaries on the rolls depends on the number of new enrollments and the number of existing beneficiaries who had not exited the program in that year. The latter quantity is indicated in Chart 1 by the vertical distance between the two blue lines (for men) and the two red lines (for women).
DI enrollments and beneficiaries on the rolls, by sex: 1986–2009
| Year | Men on the rolls | Women on the rolls | Male enrollments | Female enrollments |
|---|---|---|---|---|
| 1986 | 1.82 | 0.90 | 0.28 | 0.14 |
| 1987 | 1.85 | 0.93 | 0.28 | 0.14 |
| 1988 | 1.87 | 0.95 | 0.27 | 0.14 |
| 1989 | 1.90 | 0.99 | 0.28 | 0.15 |
| 1990 | 1.96 | 1.04 | 0.30 | 0.17 |
| 1991 | 2.06 | 1.13 | 0.34 | 0.20 |
| 1992 | 2.22 | 1.25 | 0.40 | 0.24 |
| 1993 | 2.35 | 1.37 | 0.39 | 0.24 |
| 1994 | 2.47 | 1.49 | 0.38 | 0.25 |
| 1995 | 2.56 | 1.62 | 0.38 | 0.27 |
| 1996 | 2.64 | 1.74 | 0.36 | 0.27 |
| 1997 | 2.66 | 1.84 | 0.33 | 0.26 |
| 1998 | 2.73 | 1.96 | 0.33 | 0.28 |
| 1999 | 2.79 | 2.08 | 0.34 | 0.28 |
| 2000 | 2.85 | 2.18 | 0.34 | 0.28 |
| 2001 | 2.95 | 2.32 | 0.37 | 0.32 |
| 2002 | 3.07 | 2.47 | 0.41 | 0.34 |
| 2003 | 3.22 | 2.65 | 0.42 | 0.36 |
| 2004 | 3.37 | 2.82 | 0.43 | 0.37 |
| 2005 | 3.52 | 3.00 | 0.44 | 0.39 |
| 2006 | 3.64 | 3.16 | 0.43 | 0.38 |
| 2007 | 3.77 | 3.32 | 0.44 | 0.38 |
| 2008 | 3.92 | 3.50 | 0.47 | 0.42 |
| 2009 | 4.10 | 3.69 | 0.53 | 0.46 |
The number of awards and the number of continuing disabled-worker beneficiaries have grown over time for both men and women. The growth rates were higher for female beneficiaries, although the difference by sex in the number of beneficiaries on the rolls had almost leveled off by 2009. What factors determined the growth of DI enrollment?
For the study period, I assume that in a given year, all new DI entitlements occur at the beginning of the year and that all exits occur at the end of the year. For year t, I denote by the number of disabled-worker beneficiaries on the rolls with characteristics χ, age at DI entitlement a, disability type dt, and duration on the rolls τ. Although the characteristics variable χ in this article indicates the beneficiary's sex, it can be multidimensional to incorporate ethnicity, religion, education level, and country of origin. The disability-type variable dt corresponds to the body-system categorizations used in the administrative data. The age variable a takes values from 20 to FRA. I use the more compact notation α = (χ, dt, a) to refer to a combination of characteristics χ, disability type dt, and age a. In this notation, is the number of disabled-worker enrollments of type α in year t. Let be the probability of a DI disabled-worker beneficiary of type α in current-payment status who, after being in the program for τ years, exits the program in period t because of cause c (any of the three reasons for exit). I denote by
the probability of a disabled-worker beneficiary of type α in current-payment status who, after being in the program for τ years, exits the program in period t for any of the three competing exit risks. We have for a type α = (χ, dt, a) beneficiary,
for τ = 0 and
for τ = 1, 2, …, FRA − a, where is the insured population with characteristics χ and age a in period t who have not been on the DI rolls before and is the probability of an insured worker of characteristics χ and age a entering the DI program with disability type dt in year t. Note that of the DI enrollees in year t,
will remain beneficiaries in year t + 1, and
will continue to be beneficiaries in year t + 2, and so on. As the magnitudes of the exit probabilities decline, the numbers of continuing beneficiaries over longer periods increase in the future. Moreover, because of shifts in the age distribution of the population or in the labor-force participation rate, if the number of disabled-worker beneficiaries of type α = (χ, dt, a) with smaller exit probabilities over time increases, the number of continuing beneficiaries will be higher. This will be true even if there is no growth in the number of entitlements. For instance, assume that the 1946–1964 baby boom resulted in a relatively high proportion of young workers in the 1980s, and assume that relatively younger workers who became disabled were more likely than workers overall to have types of disabilities with relatively low exit probabilities. Alternatively, suppose that some changes in the labor market, such as increases in the shares of women who are disability-insured (as occurred in the 1980s) led to increases in disabled-worker entitlements for women, whose exit probabilities are lower than men's. In each case, the DI rolls increase more rapidly than they would in the absence of those trends, producing a ripple effect of yet larger increases in the rolls in subsequent years. These scenarios could partially explain why Chart 1 shows the rolls rising after the 1980s. To find out if this is the case, it is important to compute the exit probabilities and the factors that affect the exit probabilities for various types α = (χ, dt, a) of worker beneficiaries on the DI rolls.
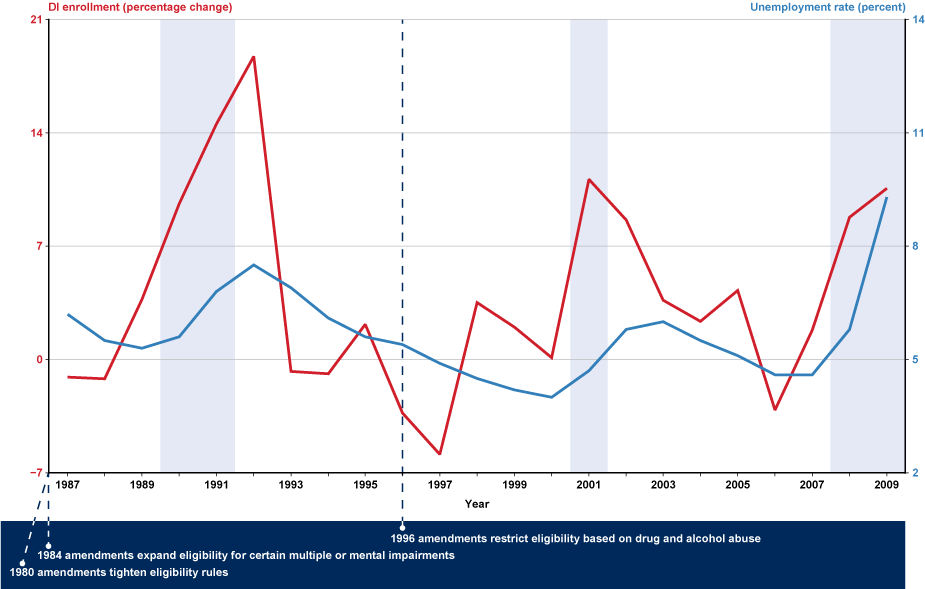
Changes in DI policies, in the macroeconomic environment (especially the unemployment rate and income distribution patterns), in the epidemiology of the disabling impairments, and in women's labor market participation and insured status are all important determinants of the growth in the DI rolls. Developments in medical technology and demographic shifts resulting from the aging of the baby boom generation likewise play important roles. Although most of these factors take effect gradually, changes in DI policies and in unemployment rates can create immediate incentives for insured workers to apply for DI benefits or discourage current DI beneficiaries from returning to work. Individual responses to such changes will lead to immediate jittery effects on the DI incidence rates and hence on the number of new DI entitlements (Chart 2).
Year-over-year percentage change in DI enrollment compared with unemployment rate for workers aged 16 or older, 1987–2009
| Year | DI enrollment (percentage change) | Unemployment rate (percent) |
|---|---|---|
| 1987 | -1.08 | 6.2 |
| 1988 | -1.18 | 5.5 |
| 1989 | 3.70 | 5.3 |
| 1990 | 9.62 | 5.6 |
| 1991 | 14.55 | 6.8 |
| 1992 | 18.73 | 7.5 |
| 1993 | -0.73 | 6.9 |
| 1994 | -0.87 | 6.1 |
| 1995 | 2.18 | 5.6 |
| 1996 | -3.31 | 5.4 |
| 1997 | -5.86 | 4.9 |
| 1998 | 3.52 | 4.5 |
| 1999 | 2.00 | 4.2 |
| 2000 | 0.12 | 4.0 |
| 2001 | 11.14 | 4.7 |
| 2002 | 8.62 | 5.8 |
| 2003 | 3.66 | 6.0 |
| 2004 | 2.36 | 5.5 |
| 2005 | 4.26 | 5.1 |
| 2006 | -3.12 | 4.6 |
| 2007 | 1.82 | 4.6 |
| 2008 | 8.79 | 5.8 |
| 2009 | 10.57 | 9.3 |
The 1980 Social Security Disability Amendments tightened the eligibility criteria for DI benefits, resulting in decreases in the number of disabled-worker entitlements in the years preceding the period covered in the chart. That downward trend was somewhat mitigated by 1984 amendments that extended DI eligibility to individuals with certain mental impairments and added eligibility criteria based on multiple impairments. The recession of 1990–1991 caused high unemployment that led immediately to sharp growth in the number of new disabled-worker entitlements. A strong economic recovery during 1995–2000 and a provision of 1996 DI amendments that disallowed benefits for individuals with a primary diagnosis of drug and alcohol abuse lowered award growth rates. The number of DI awards grew during the recession of 2001 and accelerated again during the Great Recession of 2008–2009.
Autor and Duggan (2006) suggest that growing income disparity since 1980 has raised the DI replacement rate—the portion of predisability income that DI benefits replace—for poorer workers, thus creating higher incentives for them to enter the DI rolls. In an earlier study, I estimated the effects of DI policy changes, the aggregate unemployment rate, a worker's nonemployment history, and the DI replacement rate on the incidence rate of the first DI entitlement among insured workers (Raut 2011). I will not estimate those incident rates here. In this article, I estimate the DI exit probabilities for various groups α = (χ, dt, a). Policies designed to encourage disabled-worker beneficiaries to return to work, such as the 1999 Ticket To Work initiatives, have not induced many program exits. I do not control for those policy effects in the current estimates.
Data
The data for this study come from the 2008 Continuous Work History Sample (CWHS), which is a Social Security administrative file comprising a 1 percent random sample of all workers insured under Old-Age, Survivors, and Disability Insurance.1 The CWHS contains information on the dates of DI entitlement and termination and on the reason for termination, but it does not record the date of disability onset or the type of impairment. As the best available approximation of the date of disability onset, the age at DI entitlement is used in this analysis. For information on the type of disability, I merge impairment data from administrative records known as 831 data files for entitlements from 1977 through 2006. (I use 2006 rather than 2008 as the cutoff because the CWHS requires 2 years to update the disability-related information fully. I also restrict the sample to individuals who were entitled in or after 1980.)
The CWHS for 1980–2006 contained data for 157,237 disabled-worker beneficiaries, of which 6 percent recovered, 28 percent died, 24 percent converted to retired-worker benefits because they reached FRA, and 42 percent were still on the rolls at year-end 2006. Therefore, of those who exited the program, 10 percent recovered, 48 percent died, and 42 percent retired. As estimates of exit probabilities, those figures would be biased because the individuals who exited the program during the study period do not compose a random sample. Instead, that sample overrepresents disabled individuals who were entitled during the early years of the study period and those with impairments that are more likely to lead to early exits. To compensate for those biases, it is important to incorporate the information for individuals who are still on the rolls. A competing-risks statistical model enables that inclusion, as I explain later.
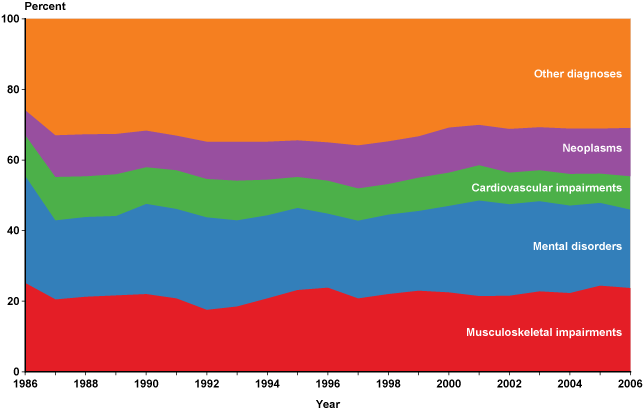
I consider five broad disability-type groupings: musculoskeletal impairments, mental disorders, cardiovascular impairments, neoplasms, and all other diagnoses. Information on primary diagnosis is available for only 108,360 of the 157,237 disabled workers in the merged sample. Chart 3 shows the percentage distribution of new entitlements by disability type for each year 1986–2006. The distributions in some years may have been affected by policy changes; for instance, analysts have suggested that changes in the mid-1980s loosened eligibility criteria for applicants with musculoskeletal impairments and mental disorders (Autor 2011; Autor and Duggan 2006; General Accounting Office 1997). Chart 3 does not reveal any striking changes in the distribution; however, its underlying data are not adjusted to account for the shifting age composition of the population over the period.
Percentage distribution of DI enrollments by diagnosis type, 1986–2006
| Year | Musculoskeletal impairments | Mental disorders | Cardiovascular impairments | Neoplasms | Other diagnoses |
|---|---|---|---|---|---|
| 1986 | 25.10 | 30.44 | 11.53 | 7.04 | 25.89 |
| 1987 | 20.47 | 22.40 | 12.37 | 11.74 | 33.02 |
| 1988 | 21.19 | 22.69 | 11.51 | 11.89 | 32.73 |
| 1989 | 21.54 | 22.64 | 11.83 | 11.37 | 32.62 |
| 1990 | 21.94 | 25.66 | 10.35 | 10.41 | 31.64 |
| 1991 | 20.69 | 25.46 | 10.96 | 9.77 | 33.12 |
| 1992 | 17.45 | 26.30 | 10.89 | 10.53 | 34.84 |
| 1993 | 18.46 | 24.46 | 11.23 | 11.05 | 34.80 |
| 1994 | 20.68 | 23.68 | 10.07 | 10.75 | 34.83 |
| 1995 | 23.10 | 23.34 | 8.79 | 10.37 | 34.39 |
| 1996 | 23.80 | 21.03 | 9.36 | 10.78 | 35.03 |
| 1997 | 20.75 | 22.07 | 9.15 | 12.23 | 35.80 |
| 1998 | 21.92 | 22.65 | 8.61 | 12.16 | 34.65 |
| 1999 | 22.90 | 22.72 | 9.40 | 11.70 | 33.27 |
| 2000 | 22.47 | 24.57 | 9.39 | 12.73 | 30.84 |
| 2001 | 21.40 | 27.10 | 10.05 | 11.46 | 30.00 |
| 2002 | 21.47 | 25.97 | 9.02 | 12.34 | 31.20 |
| 2003 | 22.72 | 25.64 | 8.70 | 12.28 | 30.67 |
| 2004 | 22.25 | 24.84 | 8.99 | 12.85 | 31.06 |
| 2005 | 24.31 | 23.54 | 8.28 | 12.82 | 31.04 |
| 2006 | 23.70 | 22.23 | 9.44 | 13.73 | 30.90 |
In the 1980s, disability incidence rates rose more rapidly for female workers and younger workers than they did for other workers (Raut 2011, Figure 3; Goss 2013, Figures 8 and 12–15). If those two groups exit the program because of death or recovery at lower-than-average rates, then the overall prevalence and duration of DI continuation will be affected, as I examine later.
Methodology
I apply the competing-risks approach to estimate exit probabilities for all causes simultaneously.2 If all disabled-worker beneficiaries in the data were observed until they exited because of death, conversion, or recovery, the exit probabilities tabulated here would simply indicate what proportion of the starting sample had exited at each duration (1 year after entitlement, 2 years after entitlement, and so on) from one of the three causes. A basic problem with all such estimates is that the data are censored because at the end point (in this case, 2006), some of the beneficiaries have not yet exited for any of the three causes. One solution involves the use of hazard rates to estimate the probability of exiting at a given duration among those who remain on the rolls. The cause-specific hazard-rate estimates can be combined to calculate what the cumulative number of exits would have been in the absence of censoring. When there are multiple causes, the hazard rates for the individual causes at each duration add up to the overall hazard rate at that duration. In the case of disabled-worker beneficiaries, in which everyone ultimately exits through one of the three causes, the cumulative share of beneficiaries who exit the program will eventually reach 100 percent; likewise, the sum of the cumulative exits from recovery, death, or conversion will also reach 100 percent.
Let be the hazard rate of exiting the program at time t for cause c, where c represents recovery, death, or conversion to retired-worker benefits.3 Let T be the random variable denoting the exit time, and let R be the random variable denoting the cause of exit. Let be the survival function—that is, the probability of surviving to time t, t > 0. The cumulative incidence function Ic (t) is the probability of exiting the program at time t or earlier for cause c, which is formally defined as
The estimation procedure of this analysis assumes a nonparametric distribution for Ic (t) for all c and applies the maximum-likelihood estimation procedure. In the present context of discrete yearly data, the maximum-likelihood estimators for the cumulative incidence functions become
where dcj = number of exits at time tj for cause c, nj is the number of people at risk at time tj, and S(tj − 1) is the Kaplan-Meier estimate of the survival function at time tj − 1. Note that in our three competing-risks cases, we have
This equation is used to estimate the survival function S(t) recursively. Notice that the competing-risks estimator of the cumulative incidence function Ic (t) depends not only on the number of individuals who exited the program for cause c but also on the number of individuals who have not exited.
In his actuarial study, Zayatz (2011) uses cells for each age-sex-duration combination, measuring age and duration of stay on the program in years. He calculates the hazard rate of exits because of recovery, death, or conversion to retired-worker benefits by age and sex during the 5-year observation period of January 1, 2001 through December 31, 2005. Because of data limitations noted earlier, I restrict my analysis to beneficiaries in the CWHS 1 percent sample who were entitled to DI from 1980 through 2000. Zayatz uses administrative data from the Master Beneficiary Record, which has information for all DI beneficiaries who were entitled to DI benefits at any time in the past and are on the program rolls during the observation period.
With that dataset, covering the entire population of 11.9 million beneficiaries, Zayatz is able to estimate the exit probabilities for each cause and for yearly ages at entitlement. With far fewer observations available, I am limited to estimating the exit probabilities for broader age-at-entitlement groups.
Recall the notation α = (χ, dt, a), in which χ represents sex, dt represents the disability type (for Zayatz, all types are combined), and a represents age at entitlement. Zayatz assumes that the exit probabilities are constant over the observation period, , as do I. In the discrete time framework of this analysis (with each year as the unit of time), his cell-frequency method is equivalent to calculating as the ratio of the number of beneficiaries of type α with τ years on the rolls who exited for cause c within a given year in the observation period to the number who were at risk of exiting. For the cells with sparse underlying data, he uses the Whitaker-Henderson two-dimensional graduation method to combine information from the nearby cells. In his dataset, however, the dates of birth, entitlement, and exit are specific days, not years. In the technical appendix to his study, he describes how he adjusts the dates to produce yearly exit-probability estimates:
The availability of complete data on each person in the study (sex, date of birth, date of entitlement, date of decrement, and cause of decrement) allows for direct estimation of the multiple-decrement probabilities q(i), where i represents the cause of decrement. Each unit age interval (x, x + 1] represents one life-year of potential exposure. For each interval that an individual is under observation, the person enters the interval at age x + r, (0 ≤ r < 1), and is scheduled to exit the interval at age x + s, (0 < s ≤ 1). Note that r = 0 except for instances where the beginning of the observation period falls within the age interval. Similarly s = 1 except for instances where the end of the observation period falls within the interval. Clearly, s − r is the amount of time that the person is scheduled to be exposed to the risks of decrement. The total scheduled exposure for an interval is obtained by summing over all persons. … Multiple-decrement probabilities are calculated by dividing the observed number of deaths or recoveries in an interval by the aggregate scheduled exposure for that interval (Zayatz 2011).
The cell-by-cell estimation of exit probabilities can be viewed as a nonparametric method that does not use information from other cells. However, if a cell in the sample has zero frequency of the event, the exit-probability estimate will be very imprecise.4 On the other hand, a fully or partially parameterized statistical model treats probabilities as varying smoothly across cells by depending on few parameters to determine the cross-cell probabilities, and the statistical estimation procedure uses data from all cells to provide smoothly varying cell-to-cell probability estimates. The problem exists even when we have disability data for the whole population, not just a sample. This is because disability incidence among an entire population is itself the realization of an epidemiological model that is presumably smooth.
Estimated Exit Probabilities
In this section, I estimate the DI exit probabilities of disabled-worker beneficiaries at three distinct levels of detail. First, I examine beneficiaries overall. Then, I examine exit-probability patterns by age at entitlement. Finally, I cross-tabulate the estimated exit probabilities by age at entitlement and sex.
Exit Patterns of the Overall Population
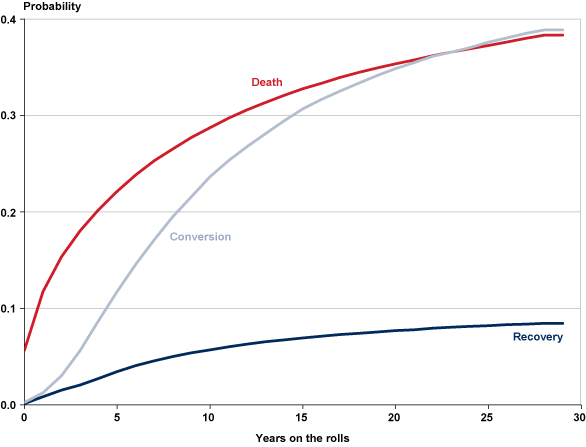
As noted earlier, this analysis is restricted to individuals who were entitled to DI disabled-worker benefits during 1980–2000. Chart 4 shows estimated exit probabilities by cause.5 Table 1 presents the probabilities for selected durations. I estimate the overall probability that an individual would exit the program because of recovery as 0.08, which is very close to the observed proportion of 0.10. The estimated exit probabilities for death and for conversion to retired-worker benefits are 0.38 and 0.39, respectively. In other words, for disabled-worker beneficiaries in a given entitlement-year cohort, 8 percent would exit the rolls because of recovery within 30 years, 38 percent would die, 39 percent would convert to retired-worker benefits, and the remaining 15 percent would still be on the rolls. (These estimates assume a constant age, sex, and disability-type composition of beneficiaries on the rolls in each year from 1980 through 2000.) Table 1 and Chart 4 also show that during the first few years of entitlement, death is the leading cause of exit, conversion to retirement is the second leading cause, and the probability of recovery is very small. Within the first year, the probability of death is more than 20 times greater than that of conversion. In Chart 4, the plot of the cumulative probability of death starts at a much higher y-level corresponding to the duration 0 on the x-axis. We will see similar patterns for most of the plots by age at entitlement, disability type, and sex later in the article. Notable exceptions involve young beneficiaries with musculoskeletal impairments or mental disorders, who have significantly higher probabilities of recovering than of dying.
| Years on the DI rolls | Recovery | Death | Conversion |
|---|---|---|---|
| 0 | 0.0013 | 0.0565 | 0.0025 |
| 1 | 0.0084 | 0.1173 | 0.0125 |
| 2 | 0.0153 | 0.1536 | 0.0302 |
| 5 | 0.0345 | 0.2214 | 0.1176 |
| 10 | 0.0570 | 0.2874 | 0.2366 |
| 15 | 0.0694 | 0.3278 | 0.3069 |
| 20 | 0.0770 | 0.3536 | 0.3487 |
| 25 | 0.0821 | 0.3726 | 0.3760 |
| 29 | 0.0845 | 0.3833 | 0.3887 |
| SOURCE: Author's calculations using Social Security administrative data and a competing-risks estimation model. | |||
The competing-risks estimates in this section assume that all disabled-worker beneficiaries have the same exit risks, irrespective of their age at entitlement, type of disability, and year of disability entitlement. It would not be surprising if recovery probabilities are higher and death probabilities are lower at younger entitlement ages. We also can expect that some types of impairment, particularly neoplasms, will have higher death rates, especially in the first few years after onset. Even the year of disability onset can affect the probabilities of recovery or death, as healthcare technology improves over time or as the health condition of program entrants changes in response to economic conditions or policy changes. I examine those factors later.
Exit Patterns by Age at Entitlement
Because the dataset is not large enough to provide reliable estimated probabilities by single year of age, I instead estimate them for four age-at-entitlement groups: 20–30, 31–40, 41–50, and 51–55. Conversion probabilities apply only to beneficiaries aged 65 or older; therefore, estimates are restricted to program exits because of death or recovery in the remainder of this analysis.
Chart 5 shows the estimated cumulative exit probabilities over the first 9 years of entitlement, and Table 2 shows the cumulative incidence probabilities by the end of 9 years in the program. Chart 5 shows that death is the dominant cause of program exit for all age groups except the youngest in the latter stages of the 9-year period. The probability of death after a given period on the rolls increases with age at entitlement. The probability of recovery is comparatively high for entitlements at ages 20–30, but declines as age of entitlement increases. Table 2 shows that after 9 years on the rolls, the combined probability of exit for either of the two causes is 29 percent for the youngest age group and 34 percent for the oldest age group. The probability of recovery is 16 percent for the youngest group but only 1 percent for the oldest group. The death probabilities have the opposite pattern: A disabled worker entitled to DI at ages 20–30 has a 13 percent probability of death within 9 years in the program; one who was entitled at ages 51–55 has a 32 percent probability.
Cumulative probability of DI program exit because of recovery or death over the first 9 years on the rolls, by age at entitlement
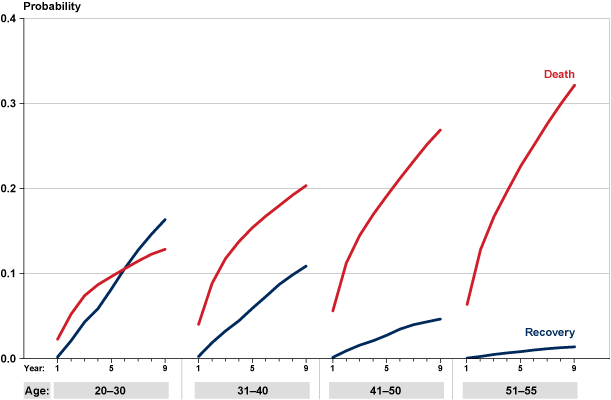
| Age group | Recovery | Death | Either recovery or death |
|---|---|---|---|
| All | |||
| 20–30 | 0.1633 | 0.1285 | 0.2918 |
| 31–40 | 0.1087 | 0.2033 | 0.3120 |
| 41–50 | 0.0465 | 0.2688 | 0.3153 |
| 51–55 | 0.0138 | 0.3214 | 0.3352 |
| Men | |||
| 20–30 | 0.1766 | 0.1425 | 0.3191 |
| 31–40 | 0.1155 | 0.2373 | 0.3527 |
| 41–50 | 0.0473 | 0.3031 | 0.3504 |
| 51–55 | 0.0131 | 0.3625 | 0.3756 |
| Women | |||
| 20–30 | 0.1403 | 0.1041 | 0.2445 |
| 31–40 | 0.0984 | 0.1520 | 0.2504 |
| 41–50 | 0.0454 | 0.2229 | 0.2683 |
| 51–55 | 0.0147 | 0.2635 | 0.2782 |
| SOURCE: Author's calculations using Social Security administrative data and a competing-risks estimation model. | |||
| NOTE: Probabilities by “either recovery or death” do not necessarily equal the sum of rounded probabilities for the separate causes. | |||
Exit Patterns by Age at Entitlement and Sex
Chart 6 plots the estimated exit probabilities over the first 9 years on the rolls by sex and shows that women exit the program because of death at lower rates than men in all age groups, and that recovery rates are lower for younger women than for younger men. For the two oldest age groups, recovery rates for men and women are almost identical.
Cumulative probability of DI program exit because of recovery or death over the first 9 years on the rolls, by sex and age at entitlement
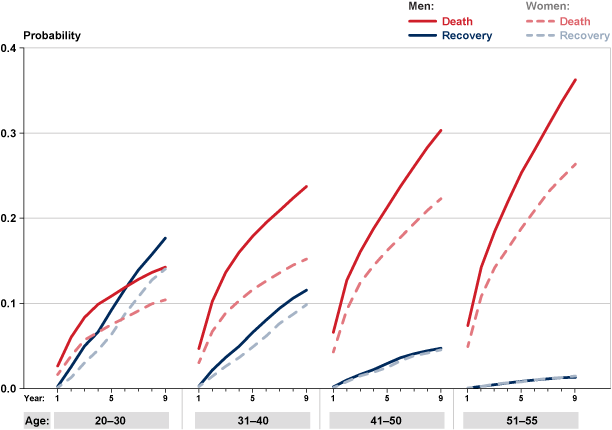
Table 2 reveals similar patterns for cumulative incidence probabilities after 9 years in the program. Overall (that is, for either of the two competing causes), exit probabilities are higher for men than for women—and the differences are more prominent at older entitlement ages: 32 percent for men versus 24 percent for women in the 20–30 age group and 38 percent for men versus 28 percent for women in the 51–55 age group. That result indicates that the labor market developments in the 1980s contributed significantly to the growth in the rolls of DI disabled-worker beneficiaries, as female enrollment rapidly increased and many women remained on the rolls for longer periods because of their lower exit probabilities.
Comparing Competing-Risks Estimates with Direct Estimates
In this section, I examine how competing-risks model estimates compare with the direct cell-frequency estimates presented in Zayatz (2011).
Comparative Estimates by Age
As described earlier, Zayatz applies a direct method to estimate the exit probabilities attributable to death and recovery. He uses data from the Master Beneficiary Record and restricts his analysis to the individuals who exited the program during 2001–2005. He computes the hazard rates of exits as the ratio of the number of individuals exiting the program during a given period to the number of workers at risk during the period. However, the definitions of the risk sets in his study differ slightly from those of this study (as detailed in the methodology section). Although Zayatz does not report cumulative incidence probabilities, I use his hazard-rate estimates to compute my cumulative incidence probabilities.6
Chart 7 plots the exit probabilities for death and recovery over the first 9 years on the rolls by estimation method and Table 3 provides the cumulative incidence probabilities through 9 years on the rolls for all, male, and female disabled-worker beneficiaries. The Zayatz direct estimates of the probability of exit because of death are slightly lower than the competing-risks model estimates, and the opposite is true for exits because of recovery, for almost all ages at entitlement. This discrepancy might stem from the use of different datasets and sample selection criteria in the two studies. Recall that this analysis restricts the years of disability entitlements to first awards in the period 1980–2000 and the observation period to 1980–2006; Zayatz considers any past years for as many as three entitlements and uses the 2001–2005 observation period. Another possible reason for the discrepancy is that exit probabilities during earlier years were in fact higher for death and lower for recovery than in later years (discussed later in this article).
Cumulative probability of DI program exit because of recovery or death over the first 9 years on the rolls, by age at entitlement: Comparing competing-risks and direct estimates
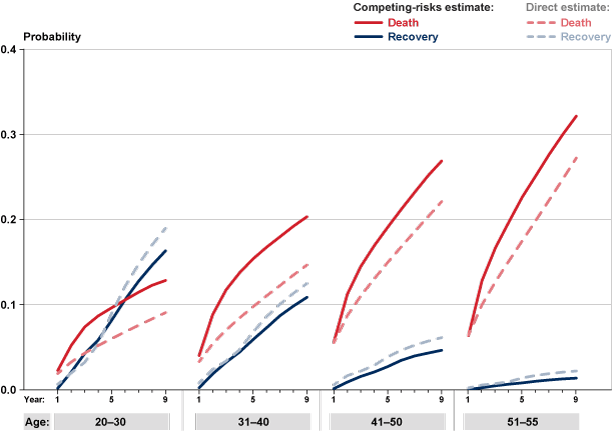
| Age group | Recovery | Death | Either recovery or death | |||
|---|---|---|---|---|---|---|
| Competing-risk estimates | Direct estimates |
Competing-risk estimates | Direct estimates |
Competing-risk estimates | Direct estimates |
|
| All | ||||||
| 20–30 | 0.1633 | 0.1897 | 0.1285 | 0.0907 | 0.2918 | 0.2804 |
| 31–40 | 0.1087 | 0.1249 | 0.2033 | 0.1466 | 0.3120 | 0.2715 |
| 41–50 | 0.0465 | 0.0613 | 0.2688 | 0.2211 | 0.3153 | 0.2824 |
| 51–55 | 0.0138 | 0.0222 | 0.3214 | 0.2722 | 0.3352 | 0.2944 |
| Men | ||||||
| 20–30 | 0.1766 | 0.2022 | 0.1425 | 0.1021 | 0.3191 | 0.3042 |
| 31–40 | 0.1155 | 0.1348 | 0.2373 | 0.1703 | 0.3527 | 0.3052 |
| 41–50 | 0.0473 | 0.0623 | 0.3031 | 0.2570 | 0.3504 | 0.3194 |
| 51–55 | 0.0131 | 0.0215 | 0.3625 | 0.3131 | 0.3756 | 0.3346 |
| Women | ||||||
| 20–30 | 0.1403 | 0.1769 | 0.1041 | 0.0790 | 0.2445 | 0.2559 |
| 31–40 | 0.0984 | 0.1146 | 0.1520 | 0.1218 | 0.2504 | 0.2364 |
| 41–50 | 0.0454 | 0.0604 | 0.2229 | 0.1833 | 0.2683 | 0.2437 |
| 51–55 | 0.0147 | 0.0228 | 0.2635 | 0.2292 | 0.2782 | 0.2520 |
| SOURCES: Author's calculations using Social Security administrative data and a competing-risks estimation model; Zayatz (2011). | ||||||
| NOTE: Probabilities by “either recovery or death” do not necessarily equal the sum of rounded probabilities for the separate causes. | ||||||
Comparative Estimates by Age and Sex
Chart 8 plots, for men and women separately, the same results that Chart 7 shows for both sexes combined. For each age-sex group, the Zayatz direct estimates of the probability of exit for either cause are close to the competing-risks estimates.
Cumulative probability of DI program exit because of recovery or death over the first 9 years on the rolls, by sex and age at entitlement: Comparing competing-risks and direct estimates
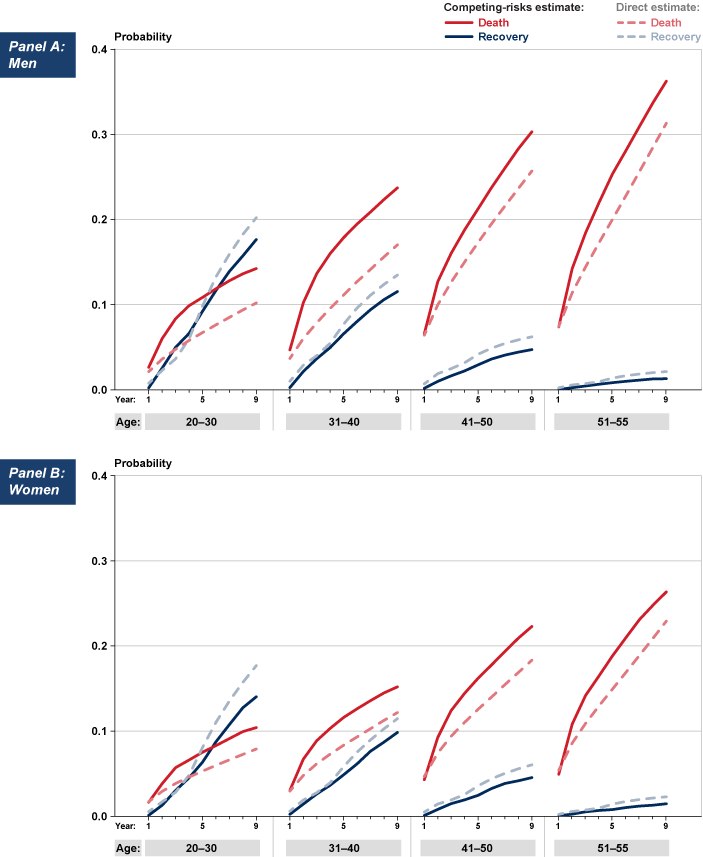
Exit Probabilities by Disability Type and Age
Exit probabilities by type of impairment may foreshadow future trends for DI. Because older people have higher propensities to encounter certain types of disabilities such as neoplasms and cardiovascular impairments, differences in exit probabilities by disability type and age at entitlement can illuminate how the advancing age of the baby boom generation will affect the disability rolls.
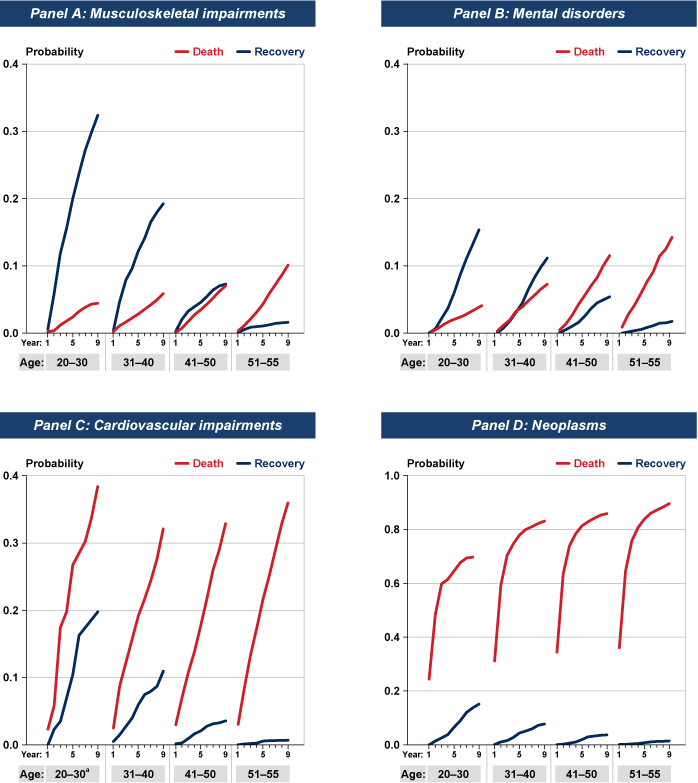
Chart 9 plots the estimated exit probabilities during the first 9 years in the program. Table 4 reports the estimated cumulative incidence of exit because of recovery or death by the end of 9 years in the program. The exit patterns for the “other diagnoses” category are very similar to the patterns for all diagnoses combined that I discussed earlier and thus “all impairments” data are omitted from Chart 9 and Table 4. The estimates for cardiovascular impairments in the 20–30 age group should be interpreted with caution because they are drawn from a very small sample (86 observations).
Cumulative probability of DI program exit because of recovery or death over the first 9 years on the rolls, by selected disability type and age at entitlement
| Disability type and age | Recovery | Death | Either recovery or death |
|---|---|---|---|
| Musculoskeletal impairments | |||
| 20–30 | 0.3237 | 0.0444 | 0.3681 |
| 31–40 | 0.1923 | 0.0586 | 0.2509 |
| 41–50 | 0.0728 | 0.0702 | 0.1431 |
| 51–55 | 0.0160 | 0.1009 | 0.1170 |
| Mental disorders | |||
| 20–30 | 0.1536 | 0.0408 | 0.1944 |
| 31–40 | 0.1115 | 0.0726 | 0.1841 |
| 41–50 | 0.0540 | 0.1151 | 0.1691 |
| 51–55 | 0.0174 | 0.1423 | 0.1596 |
| Cardiovascular impairments | |||
| 20–30 a | 0.1977 | 0.3837 | 0.5814 |
| 31–40 | 0.1095 | 0.3209 | 0.4303 |
| 41–50 | 0.0355 | 0.3286 | 0.3641 |
| 51–55 | 0.0067 | 0.3594 | 0.3661 |
| Neoplasms | |||
| 20–30 | 0.1512 | 0.6976 | 0.8488 |
| 31–40 | 0.0773 | 0.8312 | 0.9084 |
| 41–50 | 0.0369 | 0.8594 | 0.8962 |
| 51–55 | 0.0142 | 0.8960 | 0.9102 |
| Other diagnoses | |||
| 20–30 | 0.1414 | 0.2500 | 0.3914 |
| 31–40 | 0.0772 | 0.3489 | 0.4260 |
| 41–50 | 0.0382 | 0.3548 | 0.3930 |
| 51–55 | 0.0094 | 0.3703 | 0.3797 |
| SOURCE: Author's calculations using Social Security administrative data and a competing-risks estimation model. | |||
| NOTE: Probabilities by “either recovery or death” do not necessarily equal the sum of rounded probabilities for the separate causes. | |||
| a. Estimates for this age group are drawn from a small sample (86 observations) and should be interpreted with caution. | |||
For each disability type, recovery is more probable at younger ages and declines with each successively older age group. Recovery is the more probable reason for exit for the two youngest age groups with musculoskeletal system impairments and mental disorders. For the other three disability types, death is the most probable cause of exit at all ages; for neoplasms, death within the first few years is especially high. The cumulative probability of death rises with each successively older age group regardless of disability type.
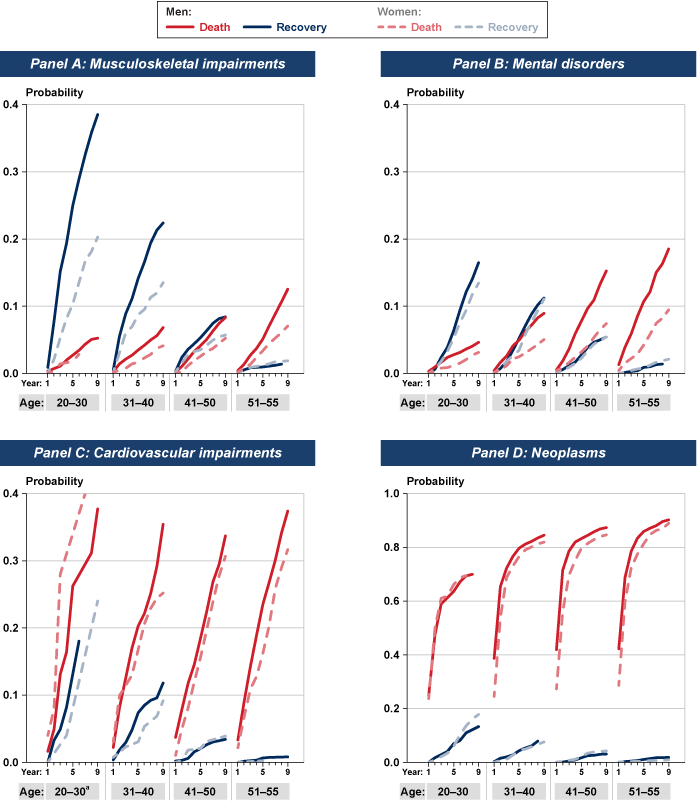
Exit Probabilities by Disability Type, Age, and Sex
Earlier, I discussed the patterns by sex of exits for all impairment types combined (see Table 2 and Chart 6). In this section, I report the estimated cumulative incidence probabilities by disability type for each age-sex combination (Table 5 and Chart 10). The general patterns that we saw for all impairments combined are very similar to those for each disability type, with two exceptions. First, for cardiovascular impairments, women who were entitled at ages 20–30 had higher exit probabilities because of death than their male counterparts had.7 Second, for neoplasms, the exit probabilities were strikingly similar for men and women regardless of cause and age at entitlement.
| Disability type and age | Recovery | Death | Either recovery or death | |||
|---|---|---|---|---|---|---|
| Men | Women | Men | Women | Men | Women | |
| All impairments | ||||||
| 20–30 | 0.1766 | 0.1403 | 0.1425 | 0.1041 | 0.3191 | 0.2445 |
| 31–40 | 0.1155 | 0.0984 | 0.2373 | 0.1520 | 0.3527 | 0.2504 |
| 41–50 | 0.0473 | 0.0454 | 0.3031 | 0.2229 | 0.3504 | 0.2683 |
| 51–55 | 0.0131 | 0.0147 | 0.3625 | 0.2635 | 0.3756 | 0.2782 |
| Musculoskeletal impairments | ||||||
| 20–30 | 0.3852 | 0.2028 | 0.0524 | 0.0285 | 0.4376 | 0.2312 |
| 31–40 | 0.2239 | 0.1351 | 0.0682 | 0.0412 | 0.2921 | 0.1762 |
| 41–50 | 0.0841 | 0.0572 | 0.0831 | 0.0524 | 0.1672 | 0.1097 |
| 51–55 | 0.0138 | 0.0188 | 0.1253 | 0.0706 | 0.1391 | 0.0893 |
| Mental disorders | ||||||
| 20–30 | 0.1648 | 0.1344 | 0.0463 | 0.0313 | 0.2111 | 0.1657 |
| 31–40 | 0.1121 | 0.1106 | 0.0894 | 0.0505 | 0.2015 | 0.1611 |
| 41–50 | 0.0541 | 0.0539 | 0.1525 | 0.0741 | 0.2066 | 0.1280 |
| 51–55 | 0.0140 | 0.0211 | 0.1852 | 0.0945 | 0.1992 | 0.1157 |
| Cardiovascular impairments | ||||||
| 20–30 a | 0.1803 | 0.2400 | 0.3770 | 0.4000 | 0.5574 | 0.6400 |
| 31–40 | 0.1181 | 0.0916 | 0.3542 | 0.2519 | 0.4723 | 0.3435 |
| 41–50 | 0.0342 | 0.0390 | 0.3369 | 0.3065 | 0.3711 | 0.3455 |
| 51–55 | 0.0081 | 0.0024 | 0.3738 | 0.3164 | 0.3820 | 0.3188 |
| Neoplasms | ||||||
| 20–30 | 0.1329 | 0.1780 | 0.6994 | 0.6949 | 0.8324 | 0.8729 |
| 31–40 | 0.0789 | 0.0759 | 0.8448 | 0.8192 | 0.9237 | 0.8951 |
| 41–50 | 0.0309 | 0.0425 | 0.8733 | 0.8462 | 0.9042 | 0.8887 |
| 51–55 | 0.0183 | 0.0092 | 0.9019 | 0.8889 | 0.9203 | 0.8980 |
| Other diagnoses | ||||||
| 20–30 | 0.1408 | 0.1426 | 0.2909 | 0.1809 | 0.4316 | 0.3235 |
| 31–40 | 0.0742 | 0.0824 | 0.4356 | 0.1982 | 0.5098 | 0.2805 |
| 41–50 | 0.0367 | 0.0401 | 0.4315 | 0.2529 | 0.4682 | 0.2930 |
| 51–55 | 0.0091 | 0.0098 | 0.4235 | 0.2966 | 0.4326 | 0.3064 |
| SOURCE: Author's calculations using Social Security administrative data and a competing-risks estimation model. | ||||||
| NOTE: Probabilities by “either recovery or death” do not necessarily equal the sum of rounded probabilities for the separate causes. | ||||||
| a. Estimates for this age group are drawn from a small sample (86 observations) and should be interpreted with caution. | ||||||
Cumulative probability of DI program exit because of recovery or death over the first 9 years on the rolls, by selected disability type, sex, and age at entitlement
Two trends specific to women appear to have contributed to the sharp rise in the number of beneficiaries on the DI rolls from 1980 through 2010. First, the combined exit probabilities because of either recovery or death for women are lower than those for men, so women tend to stay longer on the rolls. Second, in the 1980s and 1990s, the labor force participation rate of women increasingly approached that of men, as did the number of women insured for DI; as a result, DI enrollments of women increased more quickly than men's enrollments during the period. Goss (2013) contends that part of the rapid growth in the DI rolls in the 1980s could be the sharp proportional rise in the percentage of women who entered the rolls during that period. Pattison and Waldron (2013) and Liebman (2015) elaborate on those trends.8
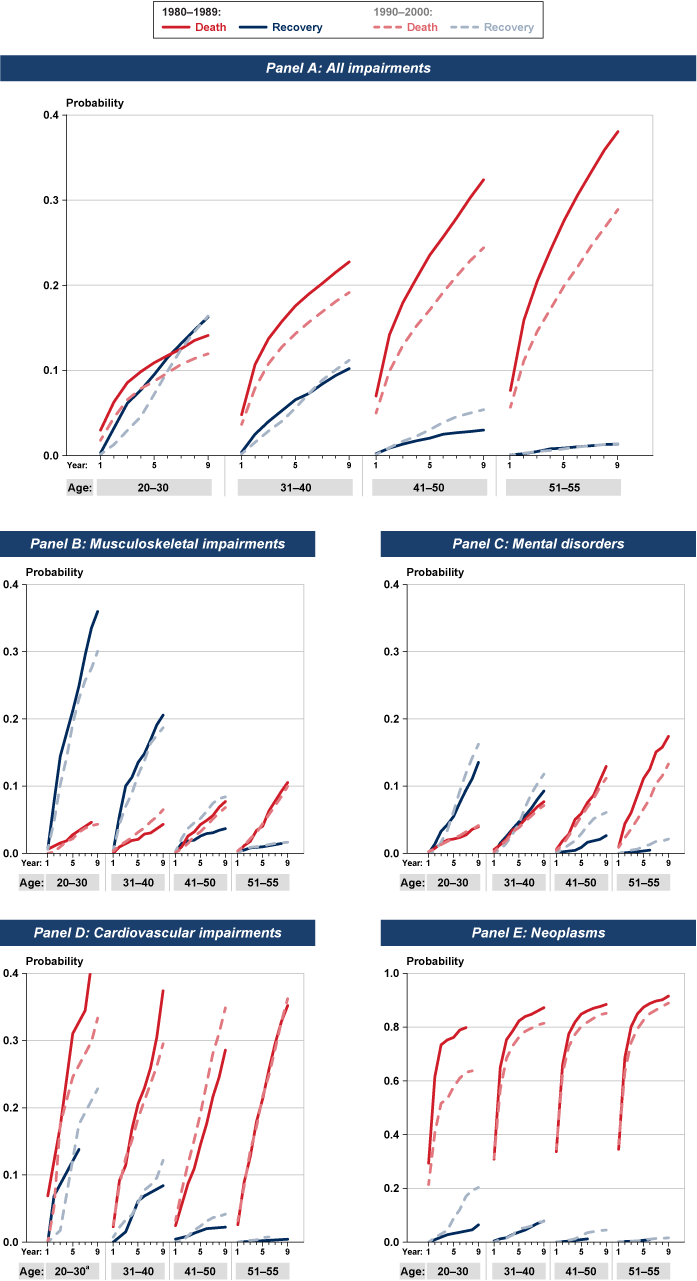
Exit Probabilities by Decade
In this section, I estimate exit probabilities by age at entitlement and disability type for two periods of entitlement: 1980–1989 and 1990–2000. Chart 11 plots the estimated exit probabilities during the first 9 years on the rolls and Table 6 reports the estimated cumulative probability of exit through 9 years in the program. (Chart 11 omits the plot for “other diagnoses” because it is very similar to that for all impairments; additionally, estimates for cardiovascular impairments in the 20–30 age group should be interpreted with caution because they reflect a small sample size.)
Cumulative probability of DI program exit because of recovery or death over the first 9 years on the rolls: For all impairments and by selected disability type and age at entitlement, 1980–1989 and 1990–2000
| Disability type and age | Recovery | Death | Either recovery or death | |||
|---|---|---|---|---|---|---|
| 1980–1989 | 1990–2000 | 1980–1989 | 1990–2000 | 1980–1989 | 1990–2000 | |
| All impairments | ||||||
| 20–30 | 0.1626 | 0.1639 | 0.1411 | 0.1196 | 0.3037 | 0.2835 |
| 31–40 | 0.1021 | 0.1119 | 0.2275 | 0.1915 | 0.3296 | 0.3034 |
| 41–50 | 0.0300 | 0.0539 | 0.3239 | 0.2441 | 0.3539 | 0.2980 |
| 51–55 | 0.0135 | 0.0139 | 0.3805 | 0.2891 | 0.3941 | 0.3030 |
| Musculoskeletal impairments | ||||||
| 20–30 | 0.3598 | 0.3006 | 0.0461 | 0.0432 | 0.4060 | 0.3438 |
| 31–40 | 0.2056 | 0.1869 | 0.0430 | 0.0649 | 0.2486 | 0.2518 |
| 41–50 | 0.0367 | 0.0840 | 0.0771 | 0.0681 | 0.1138 | 0.1521 |
| 51–55 | 0.0146 | 0.0164 | 0.1053 | 0.0998 | 0.1199 | 0.1162 |
| Mental disorders | ||||||
| 20–30 | 0.1353 | 0.1623 | 0.0395 | 0.0414 | 0.1748 | 0.2037 |
| 31–40 | 0.0926 | 0.1178 | 0.0768 | 0.0712 | 0.1694 | 0.1889 |
| 41–50 | 0.0263 | 0.0608 | 0.1292 | 0.1117 | 0.1555 | 0.1724 |
| 51–55 | 0.0046 | 0.0211 | 0.1740 | 0.1329 | 0.1787 | 0.1541 |
| Cardiovascular impairments | ||||||
| 20–30 a | 0.1379 | 0.2281 | 0.4828 | 0.3333 | 0.6207 | 0.5614 |
| 31–40 | 0.0840 | 0.1218 | 0.3740 | 0.2952 | 0.4580 | 0.4170 |
| 41–50 | 0.0223 | 0.0416 | 0.2857 | 0.3486 | 0.3080 | 0.3902 |
| 51–55 | 0.0043 | 0.0076 | 0.3521 | 0.3623 | 0.3564 | 0.3699 |
| Neoplasms | ||||||
| 20–30 | 0.0642 | 0.2033 | 0.7982 | 0.6374 | 0.8624 | 0.8407 |
| 31–40 | 0.0782 | 0.0769 | 0.8724 | 0.8144 | 0.9506 | 0.8913 |
| 41–50 | 0.0120 | 0.0449 | 0.8845 | 0.8513 | 0.8964 | 0.8962 |
| 51–55 | 0.0092 | 0.0159 | 0.9153 | 0.8893 | 0.9245 | 0.9053 |
| Other diagnoses | ||||||
| 20–30 | 0.1469 | 0.1388 | 0.2321 | 0.2587 | 0.3789 | 0.3975 |
| 31–40 | 0.0875 | 0.0739 | 0.3518 | 0.3480 | 0.4393 | 0.4218 |
| 41–50 | 0.0235 | 0.0419 | 0.3884 | 0.3464 | 0.4118 | 0.3883 |
| 51–55 | 0.0063 | 0.0103 | 0.4180 | 0.3561 | 0.4242 | 0.3664 |
| SOURCE: Author's calculations using Social Security administrative data and a competing-risks estimation model. | ||||||
| NOTE: Probabilities by “either recovery or death” do not necessarily equal the sum of rounded probabilities for the separate causes. | ||||||
| a. Estimates for this age group are drawn from a small sample (86 observations) and should be interpreted with caution. | ||||||
Chart 11 shows that from the 1980s to the 1990s, exits because of death became less common for all age groups and exits because of recovery did not improve except for ages 41–50. The former trend might be due to improvements in healthcare technology. The latter trend might reflect a shift in recent years among individuals aged 41–50 at entitlement toward impairments with lower mortality and higher recovery probabilities such as musculoskeletal impairments and mental disorders.
The probabilities of exit because of death tended to be lower in the 1990s than they were in the 1980s across disability types and age groups. Exits because of recovery did not change much in that span except for those aged 41–50 at entitlement (and for those aged 20–30 with neoplasms), for whom the recovery probabilities improved significantly. Among younger DI beneficiaries with neoplasms, the reduction in death rates and the increase in recovery rates from the 1980s to the 1990s are quite plausibly due to improvements in healthcare technology. Such improvements might be responsible for the changes seen in the other impairments as well, but an apparent improvement in health could be due to other factors, such as changing economic conditions or policies, that altered the mix of allowed applicants.
Conclusion
Using merged data from the Social Security Administration's 2008 1 percent CWHS and 831 data files, I have estimated the probabilities of DI program exit because of recovery and death. I used a nonparametric maximum-likelihood estimation procedure on a competing-risks model. Direct estimates calculated by Zayatz (2011) using Master Beneficiary Record data and a different method are, to the extent that they can be compared, similar to mine. I examined exit probabilities by cause, age at entitlement, and sex, as well as for each of five broad disability-type categories: musculoskeletal impairments, cardiovascular impairments, mental disorders, neoplasms, and all other diagnoses.
I find that during the first 9 years in the program, the dominant cause of exit for nearly all disability types is death. An exception to this pattern is seen for beneficiaries with younger entitlement ages and either musculoskeletal impairments or mental disorders, for whom the dominant cause of exit is recovery.
Women exit DI because of death at lower rates than do men at all entitlement-age groups. However, women in younger entitlement-age groups (20–40) have lower recovery rates than their male counterparts. Recovery rates at older ages do not differ much by sex. Those patterns hold for each disability type, with two exceptions: For entitlement ages 20–30, women with cardiovascular impairments exit because of death at higher rates than men do;9 and the exit rates by cause and age group for men and women with neoplasms are almost identical.
I also find that from the 1980s to the 1990s, for most disability types, probabilities of exit because of death declined while the probabilities of exit because of recovery did not increase much. The exceptions to the latter pattern are beneficiaries in the 41–50 entitlement-age group (all disability types) and those in the 20–30 entitlement-age group with neoplasms, whose recovery probabilities improved. Part of the change in the exit probabilities by cause from the 1980s to the 1990s is likely due to improvements in healthcare technology.
The findings in this article support the view that demographic shifts involving relatively younger workers, female workers, and aging workers prone to certain type of disabilities underlie some of the observed growth in the number of workers on the DI rolls.
Notes
1 For details on the CWHS, see Panis and others (2000, Chapter 10).
2 For more information on competing-risks analysis, see Fine and Gray (1999) and Pintilie (2006). For information on the estimation of various competing-risks statistical models, see Kalbfleisch and Prentice (2002).
3 More generally, we could use where is a set of variables denoting economic conditions and policy changes at time t for the beneficiary type α, cause of exit c, and year t, and βα is a vector of parameters. The policy variables could be continuous. This is another strength of using a statistical model to estimate exit probabilities.
4 Zayatz, however, uses weighted averaging of neighboring cells when he encounters a small cell frequency, as mentioned earlier.
5 I use the public-domain R package cmprsk (Gray 2014) to estimate the cumulative incidences. The standard errors for the estimated exit probabilities are omitted. The statistical model can also incorporate other regressors representing economic conditions and policy variables (Kalbfleisch and Prentice 2002). Because input data for such variables were unavailable, this analysis does not use any regressors.
6 Zayatz reports cause-specific hazard rates by age at entitlement in single years from 16 to 65, by duration in the program from 0 to 9 years, and by sex. To compare his estimates with mine, for each cause of exit, sex, and duration in the program, I average his cause-specific hazard rates for each age at entitlement to the corresponding age group in my analysis, then apply the recursive formula described in the methodology section to compute the cause-specific cumulative incidence functions. For beneficiaries overall, I apply the same approach, averaging hazard rates for men and women.
7 However, as noted earlier, this finding is based on observations of a small sample.
8 Pattison and Waldron estimate that growth in the disability-insured female population (together with other demographic changes) explains 90 percent of the growth in new DI entitlements over the period 1972–2008 and 94 percent of the growth over the subperiod 1990–2008. Lieberman examines the factors contributing to the growth in the percentage of the working-age population receiving DI benefits during 1985–2007 (nearly the same period I examine). He finds that the shifting age distribution of the population explains 28 percent of that growth for men, 15 percent for women, and 21 percent for both sexes together. Changes in the rates of workers who are insured for DI explain 3 percent for men, 18 percent for women, and 12 percent for both sexes together. Changes in the (adjusted) unemployment rate explain 57 percent for men, 45 percent for women, and 50 percent for both sexes together.
9 This finding is based on observations of a small sample and should be interpreted with caution.
References
Autor, David. 2011. “The Unsustainable Rise of the Disability Rolls in the United States: Causes, Consequences, and Policy Options.” NBER Working Paper No. 17697. Cambridge, MA: National Bureau of Economic Research.
Autor, David H., and Mark G. Duggan. 2006. “The Growth in the Social Security Disability Rolls: A Fiscal Crisis Unfolding.” Journal of Economic Perspectives 20(3): 71–96.
Fine, Jason P., and Robert J. Gray. 1999. “A Proportional Hazards Model for the Subdistribution of a Competing Risk.” Journal of the American Statistical Association 94(446): 496–509.
General Accounting Office. 1997. Social Security Disability Programs Lag in Promoting Return to Work: Report to Congressional Committee. Report No. GAO/HEHS-97-46. Washington, DC: Government Printing Office.
Goss, Stephen C. 2013. “The Financing Challenges Facing the Social Security Disability Insurance Program.” Testimony before the House Committee on Ways and Means, Subcommittee on Social Security. https://www.socialsecurity.gov/oact/testimony/HouseWM_20130314.pdf.
Gray, Robert J. 2014. “cmprsk: Subdistribution Analysis of Competing Risks.” http://cran.r-project.org/web/packages/cmprsk/index.html.
Kalbfleisch, John D., and Ross L. Prentice. 2002. The Statistical Analysis of Failure Time Data, Second Edition. Hoboken, NJ: John Wiley & Sons, Inc.
Liebman, Jeffrey B. 2015. “Understanding the Increase in Disability Insurance Benefit Receipt in the United States.” Journal of Economic Perspectives 29(2): 123–150.
Panis, Constantijn, Roald Euller, Cynthia Grant, Melissa Bradley, Christin E. Peterson, Randall Hirscher, and Paul Steinberg. 2000. SSA Program Data User's Manual. Prepared by the RAND Corporation (contract no. PM-973-SSA) for the Social Security Administration. Baltimore, MD: SSA.
Pattison, David, and Hilary Waldron. 2013. “Growth in New Disabled-Worker Entitlements, 1970–2008.” Social Security Bulletin 73(4): 25–48.
Pintilie, Melania. 2006. Competing Risks: A Practical Perspective. Hoboken, NJ: John Wiley & Sons, Inc.
Raut, Lakshmi K. 2011. “Economic Incentives and Social Security Disability Entitlements in a Counting Process Model.” Unpublished internal draft. Washington, DC: SSA, Office of Retirement and Disability Policy.
Zayatz, Tim. 2011. “Social Security Disability Insurance Program Worker Experience.” Actuarial Study No. 122. Washington, DC: Social Security Administration, Office of the Chief Actuary.