Links Between Early Retirement and Mortality
ORES Working Paper No. 93 (released August 2001)
In this paper, the author uses the 1973 cross-sectional Current Population Survey (CPS) matched to longitudinal Social Security administrative data (through 1998) to examine the relationship between retirement age and mortality for men who have lived to at least age 65 by 1997 or earlier. Logistic regression results indicate that controlling for current age, year of birth, education, marital status in 1973, and race, men who retire early die sooner than men who retire at age 65 or older. A positive correlation between age of retirement and life expectancy may suggest that retirement age is correlated with health in the 1973 CPS; however, the 1973 CPS data do not provide the ability to test that hypothesis directly.
The author is with the Division of Economic Research, Office of Research, Evaluation, and Statistics, Office of Policy, Social Security Administration.
Acknowledgments: The author would like to thank Laura Haltzel, Tom Hungerford, Howard Iams, Bert Kestenbaum, Mike Leonesio, Joyce Manchester, Jan Olson, and Jae Song for their helpful comments and suggestions. Special thanks to David Pattison and David Weaver for engaging in many discussions about this paper.
Working papers in this series are preliminary materials circulated for review and comment. The findings and conclusions expressed in them are the authors' and do not necessarily represent the views of the Social Security Administration.
Summary
In this paper I use the 1973 cross-sectional Current Population Survey (CPS) matched to longitudinal Social Security administrative data (through 1998) to examine the relationship between retirement age and mortality for men who have lived to at least age 65 by year 1997 or earlier.1 Logistic regression results indicate that controlling for current age, year of birth, education, marital status in 1973, and race, men who retire early die sooner than men who retire at age 65 or older. A positive correlation between age of retirement and life expectancy may suggest that retirement age is correlated with health in the 1973 CPS; however, the 1973 CPS data do not provide the ability to test that hypothesis directly.
Regression results also indicate that the composition of the early retirement variable matters. I represent early retirees by four dummy variables representing age of entitlement to Social Security benefits—exactly age 62 to less than 62 years and 3 months (referred to as exactly age 62 in this paper), age 62 and 3 months to 62 and 11 months, age 63, and age 64. The reference variable is men taking benefits at age 65 or older. I find that men taking benefits at exactly age 62 have higher mortality risk than men taking benefits in any of the other four age groups. I also find that men taking benefits at age 62 and 3 months to 62 and 11 months, age 63, and age 64 have higher mortality risk than men taking benefits at age 65 or older. Estimates of mortality risk for "early" retirees are lowered when higher-risk age 62 retirees are combined with age 63 and age 64 retirees and when age 62 retirees are compared with a reference variable of age 63 and older retirees. Econometric models may benefit by classifying early retirees by single year of retirement age—or at least separating age 62 retirees from age 63 and age 64 retirees and age 63 and age 64 retirees from age 65 and older retirees—if single-year breakdowns are not possible.
The differential mortality literature clearly indicates that mortality risk is higher for low-educated males relative to high-educated males. If low-educated males tend to retire early in relatively greater numbers than high-educated males, higher mortality risk for such individuals due to low educational attainment would be added to the higher mortality risk I find for early retirees relative to that for normal retirees. Descriptive statistics for the 1973 CPS show that a greater proportion of age 65 retirees are college educated than age 62 retirees. In addition, a greater proportion of age 64 retirees are college educated than age 62 retirees, and a lesser proportion of age 64 retirees are college educated than age 65 or older retirees. Age 63 retirees are only slightly more educated than age 62 retirees.
Despite a trend toward early retirement over the birth cohorts in the 1973 CPS, I do not find a change in retirement age differentials over time. However, I do find a change in mortality risk by education over time. Such a change may result from the changing proportion of individuals in each education category over time, a trend toward increasing mortality differentials by socioeconomic status, or a combination of the two.
This paper does not directly explore why a positive correlation between retirement age and survival probability exists. One possibility is that men who retire early are relatively less healthy than men who retire later and that these poorer health characteristics lead to earlier deaths. One can interpret this hypothesis with a "quasidisability" explanation and a benefit optimization explanation. Links between these interpretations and my analysis of the 1973 CPS are fairly speculative because I do not have the appropriate variables needed to test these interpretations.
A quasi-disability explanation, following Kingson (1982), Packard (1985), and Leonesio, Vaughan, and Wixon (2000), could be that a subgroup of workers who choose to take retired-worker benefits at age 62 is significantly less healthy than other workers but unable to qualify for disabled-worker benefits. An econometric model with a mix of both these borderline individuals and healthy individuals retiring at age 62 and with almost no borderline individuals retiring at age 65 could lead to a positive correlation between retirement and mortality, even if a greater percentage of individuals who retire at age 62 are healthy than unhealthy. Evidence for this hypothesis can be inferred from the finding that retiring at exactly age 62 increases the odds of dying in a unit age interval by 12 percent relative to men retiring at 62 and 3 months to 62 and 11 months for men in the 1973 CPS. In addition, retiring exactly at age 62 increases the odds of dying by 23 percent relative to men retiring at age 63 and by 24 percent relative to men retiring at age 64. A group with relatively severe health problems waiting for their 62nd birthday to take benefits could create this result.
An explanation based on benefit optimization follows Hurd and McGarry's research (1995, 1997) in which they find that individuals' subjective survival probabilities roughly predict actual survival. If men in the 1973 CPS choose age of benefit receipt based on expectations of their own life expectancy, then perhaps a positive correlation between age of retirement and life expectancy implies that their expectations are correct on average. If actuarial reductions for retirement before the normal retirement age are linked to average life expectancy and an individual's life expectancy is below average, it may be rational for that individual to retire before the normal retirement age. Evidence for this hypothesis can be inferred from the fact that men retiring at age 62 and 3 months to age 62 and 11 months, age 63, and age 64 all experience greater mortality risk than men retiring at age 65 or older. If only men with severe health problems who are unable to qualify for disability benefits are driving the results, we probably would not expect to see this result. We might expect most of these individuals to retire at the earliest opportunity (exactly age 62).2
Previous Literature
Previous research related to links between early retirement and mortality can be grouped into three main categories—studies of links between health and early retirement, studies of links between self-assessed life expectancies and subsequent mortality, and direct studies of links between early retirement and mortality.
Studies of Links Between Health and Early Retirement
In examining links between health and early retirement, many studies find poor health to be a significant factor in the retirement decision.3 Sammartino (1987), in a review of many of these studies, theorizes that workers in poor health would tend to retire at age 62. He writes (p. 37),
If the returns in expected future benefits from delaying retirement past age 62 are roughly fair for the average older worker, then they necessarily are less than fair for a worker in poor health facing less than average life expectancy. This will cause a convex kink in the budget constraint at that age, and hence a clustering of retirement at that point.
Using the New Beneficiary Survey, Packard (1985) finds that 44 percent of retired male workers first taking benefits at age 62 report a health condition limiting work compared with 28.9 percent of those retiring at age 65 and only 14.9 percent of Medicare-only beneficiaries.4 Using the New Beneficiary Survey, Packard (1985, p. 8) writes,
Retired worker beneficiaries who first received benefits at age 62 were twice as likely to report long term limitations (6 years or more) as those first receiving benefits at older ages (13 percent, compared with 6 percent). The relatively high proportion of retired-worker beneficiaries who claimed first Social Security benefits at age 62 and who reported long-term work-limiting health conditions lends support to the theory that some of those retiring at age 62 have health problems that are not severe enough to qualify them for Social Security disabled-worker benefits but that are severe enough to cause them to file for retired-worker benefits at the first opportunity.
An exception to research finding a link between poor health and early retirement is a 1996 study by Burkhauser, Couch, and Phillips using the first two waves of the Health and Retirement Study (HRS). A preliminary finding of that study is that men who take Social Security benefits at age 62 are as likely to be in poor health as men who do not (16 percent vs. 16 percent in Wave 1 and 20 percent vs. 21 percent in Wave 2)(p. 792, Table 3). However, only 27.9 percent of all males age 62 in their sample take benefits at age 62 in 1993 or 1994 as opposed to roughly 50 percent of fully insured age 62 male workers who are not disability recipients who take benefits at age 62 according to internal Social Security administrative data for 1993 and 1994.5 In addition, comparing age 62 beneficiaries to a reference variable of "postponers" may mute differences in health if relatively less healthy age 63 and age 64 retirees pull down the average health of relatively more healthy age 65 and older beneficiaries. In light of these puzzles, although the study by Burkhauser and others has the advantage of possessing more recent data than the majority of comparative studies on health and early retirement, more evidence may be needed before concluding that the traditional link between poor health and early retirement has been severed in the data of the 1990s. In particular, one might want to see independent confirmation in a contemporaneous data set.6
Leonesio, Vaughan, and Wixon (2000)—using the 1990 SIPP—find that of male Social Security beneficiaries aged 62–64, 45 percent of those who meet a modified Census Bureau definition of "severely disabled" are Old-Age and Survivors Insurance (OASI) beneficiaries and 55 percent are Disability Insurance (DI) or Supplemental Security Income (SSI) beneficiaries.7 In addition, they find that of male Social Security beneficiaries aged 62–64 who meet a stricter definition of disability simulated to approximate SSA's definition of disability, 27 percent are OASI beneficiaries and 73 percent are DI or SSI beneficiaries. Again, one would expect that the presence of a group of early OASI beneficiaries meeting definitions of severe disability should pull down the average health of early retirees versus late retirees, even if the majority of early retirees are in good health.8
Many of the studies finding poor health to be a factor in retirement use self-reported measures of health. There is some disagreement in the literature over the accuracy of self-reported health. For example, Bazzoli (1985, p. 232) argues that the effect of health on retirement is overstated because survey respondents overstate poor health to provide a socially acceptable reason for their retirement. In an empirical study of the Longitudinal Retirement History Study, she finds economic variables to be more important than health variables in the timing of retirement. In view of these disagreements, one advantage of using mortality as a measure of the correlation between poor health and retirement is its relative objectiveness.
Studies of Links Between Self-Assessed Life Expectancies and Subsequent Mortality
Hurd and McGarry (1997) use individuals' subjective survival probabilities reported in the HRS and their subsequent mortality to examine links between self-assessed life expectancies and mortality. They find that "those who survived from wave 1 to wave 2 of the HRS gave subjective survival probabilities that were about 50 percent higher than those who died between the waves (p. 17)." In addition, Hurd and McGarry (1995) find that subjective survival probabilities reported by sample respondents qualitatively follow the same pattern as known mortality differentials like sex, socioeconomic status, and smoking. Such findings are interesting because they may imply that men could be in part optimizing age of retirement benefit receipt to correspond to their estimates of their returns for delaying retirement versus their estimates of their own life expectancy, as suggested by Sammartino (1987).
Studies of Links Between Early Retirement and Mortality
A 1982 study of links between early retirement and mortality by the Social Security Administration using administrative data (the 1 percent Continuous Work History Sample (CWHS)) finds that among men reaching age 62 from 1962 to 1972 (excluding DI recipients), the proportion dying by 1978 (at ages 68 to 78) is higher for those who claim retired-worker benefits at age 62 than for those who do not. For example, among men in the 1900 birth cohort, the authors find that 58 percent of those claiming benefits at age 62 are alive at age 74, compared with 66 percent of those who did not claim benefits at age 62.
In another study, Eric Kingson (1982) uses the National Longitudinal Survey to compare the mortality of men who withdrew from the labor force before age 62 and received Social Security disability benefits with that of two other groups: men who withdrew from the labor force before age 62 and reported a work-limiting health condition before withdrawal but did not receive Social Security disability benefits and men who withdrew before age 62, did not receive a disability benefit, and did not report a health limitation. Among white males in these three groups, he finds that 33 percent of the disability recipients are dead by 1975, 42 percent of the nondisability recipients who reported a health limitation are dead by 1975, and 15 percent of the nondisability recipients who reported no health limitations are dead by 1975. Evidence of a group of unhealthy workers waiting until age 62 to claim retirement benefits could be one factor contributing to the apparent link between early retirement and mortality in the updated 1973 Exact Match. However, to accept Kingson's findings as evidence for mortality and retirement age linkages in the 1973 CPS, one must assume that most of the men who dropped out of the labor force before age 62 and did not receive disability benefits would qualify for retirement benefits under the quarters of coverage requirement and claim them at age 62.
In the 1990s, using administrative data from the Canadian Pension Plan (CPP), Wolfson and others (1993) find lower survival probabilities for early retirees (those whose last year of earnings was at age 61 or younger) than later retirees at almost all earning levels. They also find higher earnings are associated with later retirement. In addition, separate multivariate Weibull regressions run for each age of retirement exhibit a pattern following a "generally positive association between survival probability and age of retirement (S175)."9
Data Description
This study uses a version of the 1973 Exact Match in which data from the 1973 Current Population Survey are matched to Social Security administrative records. The matched Social Security administrative data have been updated by Bert Kestenbaum and Chris Chaplain, in SSA's Office of the Chief Actuary, to include longitudinal earnings from 1951 to 1996 (Master Earnings File), beneficiary and claim data from the date of the respondent's entitlement up to mid-1998 (Master Beneficiary Records), and death data (Numident, Master Beneficiary Records, and Master Earnings File).10 There are 85,882 persons in the file with good matches to Social Security administrative data. Of these persons, 44,603 are identified as beneficiaries, 21,404 of whom are male. In order to restrict the sample to retired-worker male beneficiaries, disability recipients are eliminated from the sample. The sample is further restricted by birth cohort, resulting in a final sample of 10,938 retired-worker male beneficiaries with a retirement age of at least 62 who survived until at least age 65. By restricting the sample to men surviving to at least 65, 196 men who died from age 62 to age 64 are eliminated. Thus, the sample used for this analysis is likely to be both healthier than the total Social Security beneficiary population (retired workers plus disabled workers) and slightly healthier than the total retired-worker population.11 Beneficiaries in the sample are born from 1906 to 1932, so they are aged 41–67 at the time of the 1973 survey and aged 65–91 in 1997, the cutoff year for the death data in this study.12 The following tabulation provides a summary of the 1973 Exact Match sample.
| Characteristic | Number |
|---|---|
| Persons with good matches | 85,882 |
| Beneficiaries | 44,603 |
| Male beneficiaires | 21,404 |
| Retired male beneficiaries born from 1906 to 1932 | 11,134 |
| Retired male beneficiaries surviving to age 65 | 10,938 |
| Born from— | |
| 1906 to 1909 | 1,437 |
| 1910 to 1913 | 1,449 |
| 1914 to 1917 | 1,532 |
| 1918 to 1921 | 1,775 |
| 1922 to 1925 | 1,774 |
| 1926 to 1929 | 1,712 |
| 1930 to 1932 | 1,259 |
| Entitled at age— | |
| 62.0 months to less than 62 and 3 months (exactly 62) | 4,089 |
| 62 and 3 months to 62 and 11 months | 1,132 |
| 63 to 63 and 11 months | 1,113 |
| 64 to 64 and 11 months | 2,112 |
| 65 or older | 2,492 |
This study uses 1973 educational attainment as its primary socioeconomic variable. In future work, I hope to create an earnings variable to estimate the correlation of earnings and mortality and to more accurately gauge the strength of the earnings variable vis-à-vis the other independent variables.13 Since Wolfson and others (1993) found that a greater proportion of low-income individuals tend to retire early than high-income individuals and since many studies have found mortality differentials based on income, it is possible that the inclusion of an earnings variable would reduce the magnitude of the retirement-age coefficients reported. (On the other hand, because educational attainment occurs early in a worker's life, its level may be less affected by poor health than an earnings variable that could reflect poor health reducing earnings before retirement, rather than low earnings leading to poor health. Therefore, education may be a cleaner socioeconomic proxy in the sense that there may be less reverse causation between poor health and level of educational attainment.)
The model I use to estimate the variables described below is a discrete time logistic regression. The dependent variable is a censored binary variable that equals 1 if an individual dies in the observation period (1973–1997) and 0 if the individual is alive at the end of the observation period (1997). The model measures the logit or log odds of dying using the maximum likelihood method of estimation. The parameter estimates measure the rate of change in the logit (log of the odds) due to a one-unit change in the explanatory variable, controlling for the effects of the other variables.
Dependent Variable
Observations begin in the year the worker turns age 65 and end in the earlier of the year of death or December 1997. The dependent variable is equal to 1 in the year the worker dies and 0 in every year the worker survives. Of the 10,938 workers in the sample alive at age 65, 4,425 are dead by the end of the sample period in 1997. Counting all annual observations for the 10,938 workers, there are 4,425 years in which a worker died and 107,319 years in which a worker survived, for a total of 111,744 pooled observations.
The regression estimates reported are logit regressions on these 111,744 observations. A given worker in the sample has up to 26 observations (for a worker age 67 in 1973 who is not dead by 1997), with either 0 or 1 death observation. The explanatory variables for a given worker are constant except for the age variable, which is time-varying. The age variable increases each year (observation) after age 65 until 1997 (maximum age of 91 for a worker who is born in 1906) or death. All regressions estimated use unweighted data.14
Explanatory Variables
- Current age from age 65 to death or to year 1997 is used to estimate the effect of age on mortality risk. Current age is a censored variable because the measurement of current age ends in 1997. Therefore, censoring increases with birth cohort.
- Because mortality has improved over time and the sample contains birth cohorts spanning 26 years, a continuous year-of-birth variable is used to estimate an independent cohort or period effect on mortality risk.
- Marital status in 1973 is used to approximate a measure of the effect of marriage on mortality risk. Unfortunately, the data file provides only a point-in-time measure of marriage. Therefore, this variable does not have the explanatory power of a marriage variable, like current marital status, that changes over time. However, in exploratory data analysis of the 1973 Exact Match for respondents aged 41 to 67 in 1973, the percentage who never married had leveled off at about 5 percent of the full sample. Thus, because of the age of the sample, this variable may be a reasonable approximation of whether a respondent has ever been married; however, it cannot answer the question of whether a respondent has subsequently divorced or been widowed. Since both these states have been found to affect mortality risk in many studies, it is important to interpret marital estimates as a function of marital status in 1973, not current marital status.
- Race data in the 1973 CPS include the categories white, African American, and other. Estimates are only made for the effect of being African American on mortality risk.
- Education, recorded in the CPS in single years, is grouped into three categories for estimation: less than 12 years of school (less than high school), 12–15 years of school (high school graduate), and 16 or more years of school (college graduate).
- The retirement age (the Social Security age of entitlement) of each beneficiary, measured in months, is grouped into five categories for estimation: exactly 62.0 years to less than 62 years and 3 months (referred to as exactly age 62), 62 and 3 months to 62 and 11 months, 63 to 63 and 11 months, 64 to 64 and 11 months, and greater than or equal to 65 years. Beneficiaries are first eligible to retire at age 62.
Descriptive Statistics
Before performing regression analysis, I examine the distribution of the sample by some of the explanatory variables (see Table 1). The final column gives the estimated probability that an individual will not die until age 80 or later for each subgroup, given survival to age 65. The survival estimates are obtained using the life-table (actuarial) method.15 For the full sample, given survival to age 65, there is a 69 percent probability that an individual will not die until age 80 or older. Examining survival probabilities for various subsamples, several patterns emerge. Survival probability increases by education, with a difference of 7 percentage points between those with less than 12 years of education and those with at least 16 years of education. Beneficiaries married in 1973 have a 3-percentage-point greater chance of surviving to age 80 than the "never married" in 1973, and men divorced or separated in 1973 have a 9-percentage-point lower chance of surviving to age 80. Whites in the sample have a 5-percentage-point greater probability of surviving to age 80 than African Americans. Results by retirement-age category are perhaps the most striking. Those retiring at age 65 or greater have an 11-percentage-point greater probability of surviving to age 80 than those retiring at exactly age 62. Note that collapsing all early retirees into one category shrinks this difference by 4 percentage points, because the lower survival probability of men retiring at exactly age 62 (63 percent) is averaged in with the higher survival probabilities of men retiring at age 62 and 3 months to 62 and 11 months, age 63, and age 64 (67 percent, 70 percent, and 71 percent, respectively).
| Sample | N | Percentage of sample | Survival probability to age 80 |
|---|---|---|---|
| Full sample | 10,938 | 100.0 | 0.69 |
| Education | |||
| Less than 12 | 4,308 | 39.4 | 0.67 |
| 12–15 | 4,855 | 44.4 | 0.71 |
| 16 or more | 1,775 | 16.2 | 0.74 |
| Marital status in 1973 | |||
| Married | 9,754 | 89.2 | 0.70 |
| Divorced or separated | 459 | 4.2 | 0.61 |
| Widowed | 245 | 2.2 | 0.66 |
| Never married | 480 | 4.4 | 0.67 |
| Age at entitlement | |||
| 62.0 to less than 65 | 8,446 | 77.2 | 0.67 |
| 62.0 to less than 62 and 3 months (exactly 62) | 4,089 | 37.4 | 0.63 |
| 62 and 3 months to 62 and 11 months | 1,132 | 10.4 | 0.67 |
| 63 to 63 and 11 months | 1,113 | 10.2 | 0.70 |
| 64 to 64 and 11 months | 2,112 | 19.3 | 0.71 |
| 65 or older | 2,492 | 22.8 | 0.74 |
| Race | |||
| African American | 654 | 6.0 | 0.64 |
| White | 10,187 | 93.1 | 0.69 |
| SOURCE: Author's calculations on the 1973 Exact Match. | |||
| NOTE: Sample counts, percentages, and survival probabilities are unweighted. Weighted statistics might differ. | |||
One can further examine the composition of beneficiaries in different retirement age categories by examining their selected characteristics. In Table 2, the most interesting observation may be the contrast in education between the group retiring at exactly age 62 and the group retiring at age 65 or older. Comparing the two groups, the latest retirees have 11 percentage points fewer men at the lowest education level than the earliest retirees. The latest retirees also have 14 percentage points more men at the highest education level than the earliest retirees.16
| Variable | Full sample | 62.0–62.24 | 62.25–62.9 | 63–63.9 | 64–64.9 | 65+ |
|---|---|---|---|---|---|---|
| Education (years) | ||||||
| Less than 12 | 40.3 | 43.0 | 46.3 | 43.9 | 40.1 | 31.6 |
| 12–15 | 43.6 | 45.1 | 42.2 | 42.3 | 43.4 | 42.6 |
| 16 or more | 16.1 | 11.9 | 11.6 | 13.7 | 16.5 | 25.8 |
| Married in 1973 | 87.3 | 85.4 | 88.4 | 86.3 | 88.9 | 89.2 |
| Race | ||||||
| African American | 7.7 | 7.7 | 11.0 | 8.6 | 6.8 | 6.5 |
| White | 91.2 | 91.7 | 87.8 | 90.6 | 91.3 | 92.1 |
| Percentage of full sample | 100.0 | 37.5 | 10.5 | 10.2 | 19.3 | 22.5 |
| SOURCE: Author's calculations on the 1973 Exact Match. | ||||||
| NOTE: Percentages are based on a weighted sample using the "Final" CPS-IRS-SSA stats unit administrative weight in the 1973 Exact Match. | ||||||
Regression Analysis
To examine the relationship between retirement age and mortality, it is necessary to control for other explanatory variables that may affect mortality risk. For example, the descriptive statistics on the 1973 Exact Match suggest that people retiring at age 65 or older tend to be more educated than earlier retirees. Since we expect education to be negatively correlated with mortality, differences in survival probability to age 80 between early and late retirees could result from differences in educational attainment between the two groups. If differences in survival probability between early and late retirees remain after controlling for education, then we can conclude that there is some residual difference in mortality risk factors between the two groups.
This study estimates the effect of current age, birth cohort, education, marital status in 1973, race, and retirement age on the log odds of dying. As described below, the regression results for the retirement-age variables follow the same pattern as the life-table estimates of survival probability by retirement age reported previously. Mortality risk decreases with an increase in the age at which an individual in the sample retires, even when controlling for current age, year of birth, marital status, education, and race, thus suggesting an independent relationship between retirement age and mortality risk. If retirement age is correlated with health, then one might expect such a result.
The parameter estimates in Table 3 can be interpreted as the change in the log-odds of dying associated with an increase of one unit in the explanatory variable (for example, age, year of birth) or the change in the log odds of dying associated with an individual being in a dummy (1 or 0) variable category relative to the reference category for that dummy variable.17 In equation 4, retiring at exactly age 62 (retage1) increases the log odds of dying by 0.3232 relative to those retiring at age 65 or older (retage5), holding all the other variables constant. Relative to those retiring at age 65 or older, retiring at age 62 and 3 months to 62 and 11 months (retage2) increases the log odds of dying by 0.2113, retiring at age 63 (retage3) increases the log odds by 0.1174, and retiring at age 64 (retage4) increases the log odds of dying by 0.1089. All explanatory variables are significant at the 5 percent level.
| Variable | Equation 1 | Equation 2 | Equation 3 | Equation 4 | ||||
|---|---|---|---|---|---|---|---|---|
| Parameter estimate | Odds ratio (confid. intervals) | Parameter estimate | Odds ratio (confid. intervals) | Parameter estimate | Odds ratio (confid. intervals) | Parameter estimate | Odds ratio (confid. intervals) | |
| Intercept | 6.5533 (5.8017) |
n.a. | 4.7429 (5.8072) |
n.a. | 5.0343 (5.8070) |
n.a. | 13.6958 (5.9356) |
n.a. |
| Age | 0.0947 (0.0029)* |
1.099 (1.093–1.106) |
0.0953 (0.0029)* |
1.10 (1.094–1.106) |
0.0954 (0.0029)* |
1.10 (1.094–1.106) |
0.0961 (0.00291)* |
1.10 (1.095–1.107) |
| Year of birth | -0.00884 (0.00297)* |
0.991 (0.985–0.997) |
-0.00779 (0.00298)* |
0.992 (0.986–0.988) |
-0.00795 (0.00298)* |
0.992 (0.986–0.988) |
-0.0126 (0.00305)* |
0.988 (0.982–0.993) |
| Edu1 | 0.4110 (0.052)* |
1.508 (1.362–1.67) |
0.4018 (0.052)* |
1.495 (1.35–1.655) |
0.3913 (0.0522)* |
1.479 (1.335–1.638) |
0.3182 (0.0533)* |
1.375 (1.238–1.526) |
| Edu2 | 0.2114 (0.053)* |
1.235 (1.114–1.371) |
0.2124 (0.053)* |
1.237 (1.115–1.372) |
0.2124 (0.053)* |
1.237 (1.115–1.372) |
0.166 (0.0535)* |
1.181 (1.063–1.311) |
| Married in 1973 | n.a. | n.a. | -0.2865 (0.0449)* |
0.751 (0.688–0.820) |
-0.2776 (0.0451)* |
0.758 (0.694–0.828) |
-0.2588 (0.0452)* |
0.772 (0.706–0.844) |
| African American | n.a. | n.a. | n.a. | n.a. | 0.151 (0.0628)* |
1.163 (1.028–1.315) |
0.156 (0.0629)* |
1.169 (1.033–1.322) |
| Retage1 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 0.3232 (0.0428)* |
1.382 (1.27–1.503) |
| Retage2 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 0.2113 (0.0586)* |
1.235 (1.101–1.386) |
| Retage3 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 0.1174 (0.0567)* |
1.125 (1.006–1.257) |
| Retage4 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 0.1089 (0.0476) |
1.115 (1.016–1.224) |
| -2Log likelihood | 35632.56 | n.a. | 35594.235 | n.a. | 35588.663 | n.a. | 35525.99 | n.a. |
| Latent R 2 | 0.0879 | n.a. | 0.0898 | n.a. | 0.0901 | n.a. | 0.0945 | n.a. |
| SOURCE: Author's calculations on the 1973 Exact Match. | ||||||||
| NOTES: n.a. = not applicable. | ||||||||
| * = standard error significant at the 5 percent level. | ||||||||
| age = age from age 65 until death or year 1997 | ||||||||
| year of birth = year of birth | ||||||||
| edu1 = 1 if < 12 years of education | ||||||||
| edu2 = 1 if 12–15 years of education | ||||||||
| Reference variable (edu3) = 1 if 16+ years of education | ||||||||
| married = 1 if married in 1973 | ||||||||
| Reference variable = not married in 1973 | ||||||||
| African American = 1 if African American | ||||||||
| Reference variable = not African American | ||||||||
| retage1 = 1 if retirement age <62.25 | ||||||||
| retage2 = 1 if retirement age >=62.25 and <=62.9 | ||||||||
| retage3 = 1 if retirement age >=63 and <=63.9 | ||||||||
| retage4 = 1 if retirement age >=64 and <=64.9 | ||||||||
| Reference variable (retage5) = 1 if retirement age >=65 | ||||||||
The odds ratios reported for each equation provide another way of interpreting the logistic results.18 Perhaps the most striking odds ratio is the 38 percent greater odds of dying for those retiring at exactly age 62 relative to those retiring at age 65 or older in equation 4. This may suggest that people in poorer health are more likely to claim benefits as soon as they possibly can (age 62). Note that having less than 12 years of education (edu1) also increases the odds of dying by about 38 percent relative to men with 16 or more years of education. In magnitude, the relative odds of dying appear similar for these two states. In addition, relative to men retiring at age 65 or older, I find a 23.5 percent increase in the log odds of dying for men retiring at age 62 and 3 months to age 62 and 11 months, a 12.5 percent increase for men retiring at age 63, and an 11.5 percent increase for men retiring at age 64.
Comparing the parameter estimates of equation 3 and equation 4, the introduction of the retirement-age variables reduces the effect of edu1 by about 0.07 and edu2 by about 0.05. Since the descriptive statistics for the 1973 Exact Match suggest that men retiring later are more likely to be more educated, the education coefficients in absence of the retirement-age variables may be picking up some of their proxy health effects.
Composition of the Retirement-Age Variables
An advantage of the detailed administrative data in the 1973 Exact Match is that they allow one to test for how the composition of the variable(s) for early retirement age affects analytical results. I conduct two different types of tests to determine whether analyzing retirees aged 62 to 64 by four dummy variables yields more information than collapsed "early" retirement-age categories. First, I conduct contrast tests to see whether the four dummy variables representing early retirees (exactly age 62, age 62 and 3 months to age 62 and 11 months, age 63, and age 64) are significantly different from each other. Second, I create less detailed retirement-age categories and observe how the regression coefficients change as those retirement-age categories change. Both tests indicate that analytical results are sensitive to the composition of the retirement-age variables and that there appears to be a significant difference between men taking benefits right at age 62 and all other retired-worker beneficiaries.
I have already compared the four retirement-age dummy variables with men retiring at age 65 or older (see Table 3, equation 4). Using contrast tests, I now compare retiring at exactly age 62 (retage1) with a reference variable of retiring at age 62 and 3 months to 62 and 11 months (retage2), with a reference variable of retiring at age 63 (retage3), and with a reference variable of retiring at age 64 (retage4). I also compare retiring at age 62 and 3 months to 62 and 11 months with retiring at age 63 and at age 64. Finally, I compare retiring at age 63 with retiring at age 64.
Results of these comparisons show that retage1 is significantly different from retage2, retage3, and retage4 at the 5 percent level (see Table 4). Retage2 is significantly different from retage4 at the 10 percent level, although the confidence interval crosses one. Retage2 is not significantly different from retage3, and retage3 is not significantly different from retage4. Of course, it is important to remember that sample size is not equal between these dummy variables. retage1=37 percent of the sample, retage2=11 percent of the sample, retage3=10 percent of the sample, and retage4=20 percent of the sample, which could affect significance tests.
| Contrast | Odds ratio (standard errors) | Confidence intervals |
|---|---|---|
| retage1 vs. retage2 | 1.1184 (0.0616)* |
1.004–1.2458 |
| retage1 vs. retage3 | 1.2286 (0.0661)* |
1.1056–1.3653 |
| retage1 vs. retage4 | 1.239 (0.0545)* |
1.1366–1.3506 |
| retage2 vs. retage3 | 1.0985 (0.0738) |
0.9629–1.2531 |
| retage2 vs. retage4 | 1.1078 (0.0661)** |
0.9856–1.2451 |
| retage3 vs. retage4 | 1.0085 (0.0588) |
0.8996–1.1304 |
| SOURCE: Author's calculations on the 1973 Exact Match. | ||
| NOTES: | ||
| * = standard error significant at the 5 percent level; | ||
| ** = standard error significant at the 10 percent level. | ||
The strength of retage1 is perhaps somewhat surprising. An apparent difference between the earliest retirees (men taking benefits at exactly age 62) versus men retiring at age 62 and 3 months to age 62 and 11 months seems to suggest there may be a group taking benefits at the first opportunity who are in particularly ill health or who have a short life expectancy relative to other workers. (Note, however, that the confidence interval for the odds ratio estimate ranges from 1.004 to 1.2458—the low estimate being not very far from 1—and that the confidence bands for retage1 and retage2 overlap.) Retiring at exactly age 62 increases the odds of dying by 12 percent relative to men retiring at age 62 and 3 months to 62 and 11 months, by 23 percent relative to men retiring at age 63, and by 24 percent relative to men retiring at age 64.
Because survey data not linked to Social Security Master Beneficiary Records often do not report age of entitlement in as fine detail, it is possible that some of the differences between retirement age categories are masked when retirement-age categories are collapsed. Results show that the magnitude of the mortality differential for those in the "earliest" retirement-age category is attenuated as the definition of "early" changes with the composition of the retirement-age categories (see Table 5). With five categories for age of retirement (equation 4), the parameter estimate on the earliest category is 0.3232 and the odds ratio is 1.38. Combining men retiring at exactly age 62 with men retiring from age 62 and three months to 62 and 11 months (equation 4a) lowers the parameter estimate on the earliest category to 0.2958 and the odds ratio to 1.34. Combining all men retiring before age 65 into an "early retiree" category (equation 4b) lowers the parameter estimate to 0.211 and the odds ratio to 1.24. Comparing men who have a retirement age of 62 with a reference variable of men retiring at age 63 or older (equation 4c) lowers the parameter estimate to 0.2313 and the odds ratio to 1.26.
| Variable | Equation 4 | Equation 4a | Equation 4b | Equation 4c | ||||
|---|---|---|---|---|---|---|---|---|
| Parameter estimate | Odds ratio (confid. intervals) | Parameter estimate | Odds ratio (confid. intervals) | Parameter estimate | Odds ratio (confid. intervals) | Parameter estimate | Odds ratio (confid. intervals) | |
| Intercept | 13.6958 (5.9356) |
n.a. | 13.3109 (5.9321) |
n.a. | 10.2752 (5.8975) |
n.a. | 11.9805 (5.9007) |
n.a. |
| Age | 0.0961 (0.00291)* |
1.10 (1.095–1.107) |
0.0961 (0.00291)* |
1.101 (1.095–1.107) |
0.0958 (0.00291)* |
1.101 (1.095–1.107) |
0.0960 (0.00291)* |
1.101 (1.094–1.107) |
| Year of birth | -0.0126 (0.00305)* |
0.998 (0.982–0.993) |
-0.0124 (0.00304)* |
0.988 (0.982–0.994) |
-0.0108 (0.00303)* |
0.988 (0.982–0.994) |
-0.0116 (0.00303)* |
0.988 (0.983–0.994) |
| Edu1 | 0.3182 (0.0533)* |
1.375 (1.238–1.526) |
0.3182 (0.0533)* |
1.375 (1.238–1.526) |
0.333 (0.0532)* |
1.375 (1.238–1.526) |
0.338 (0.0528)* |
1.402 (1.264–1.555) |
| Edu2 | 0.166 (0.0535)* |
1.181 (1.063–1.311) |
0.1656 (0.0535)* |
1.18 (1.063–1.31) |
0.1722 (0.0534)* |
1.18 (1.063–1.31) |
0.18 (0.0532)* |
1.197 (1.079–1.329) |
| Married in 1973 | -0.2588 (0.0452) |
0.772 (0.706–0.844) |
-0.2627 (0.0452)* |
0.772 (0.704–0.84) |
-0.27 (0.0451)* |
0.772 (0.704–0.84) |
-0.2642 (0.0452)* |
0.768 (0.703–0.839) |
| African American | 0.156 (0.0629)* |
1.169 (1.033–1.322) |
0.1536 (0.0629)* |
1.169 (1.031–1.319) |
0.1491 (0.0629)* |
1.169 (1.031–1.319) |
0.1554 (0.0629)* |
1.168 (1.033–1.321) |
| Retage1 | 0.3232 (0.0428)* |
1.382 (1.27–1.503) |
n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| Retage2 | 0.2113 (0.0586)* |
1.235 (1.101–1.386) |
n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| Retage3 | 0.1174 (0.0567)* |
1.125 (1.006–1.257) |
n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| Retage4 | 0.1089 (0.0476)* |
1.115 (1.016–1.224) |
n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| Retage62 | n.a. | n.a. | 0.2958 (0.041)* |
1.344 (1.241–1.456) |
n.a. | n.a. | n.a. | n.a. |
| Retage63 | n.a. | n.a. | 0.117 (0.0567)* |
1.124 (1.006–1.256) |
n.a. | n.a. | n.a. | n.a. |
| Retage64 | n.a. | n.a. | 0.1086 (0.0476)* |
1.115 (1.015–1.224) |
n.a. | n.a. | n.a. | n.a. |
| Retage early | n.a. | n.a. | n.a. | n.a. | 0.211 (0.0374)* |
1.235 (1.148–1.329) |
n.a. | n.a. |
| Retage 62 only | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 0.2313 (0.0321)* |
1.26 (1.183–1.342) |
| -2Log likelihood | 35525.99 | n.a. | 35530.2 | n.a. | 35555.857 | n.a. | 35537.066 | n.a. |
| Latent R 2 | 0.0945 | n.a. | 0.09442 | n.a. | 0.0926 | n.a. | 0.0936 | n.a. |
| SOURCE: Author's calculations on the 1973 Exact Match. | ||||||||
| NOTES: n.a. = not applicable. | ||||||||
| * = standard error significant at the 5 percent level. | ||||||||
| age = age from age 65 until death or year 1997 | ||||||||
| year of birth = year of birth | ||||||||
| edu1 = 1 if 0–11 years of school (less than a high school diploma) | ||||||||
| edu2 = 1 if 12–15 years of school (high school graduate to 3 years of college) | ||||||||
| Reference variable (edu3) = 1 if 16+ years of school (4+ years of college) | ||||||||
| married = 1 if married in 1973 | ||||||||
| Reference variable = not married in 1973 | ||||||||
| African American = 1 if African American | ||||||||
| Reference variable = not African American | ||||||||
| retage1 = 1 if retirement age <62.25; retage2 = 1 if retirement age >=62.25 and <=62.9 | ||||||||
| retage3 = 1 if retirement age >=63 and <=63.9; retage4 = 1 if retirement age >=64 and <=64.9 | ||||||||
| Reference variable (retage5) = 1 if retirement age >=65 | ||||||||
| retage62 = 1 if retirement age < 63; Retage63 = 1 if retirement age >= 63 and < 64; Retage64 = 1 if retirement age >= 64 and < 65 | ||||||||
| Reference variable (retage65) = 1 if retirement age >= 65 | ||||||||
| retage early = 1 if retirement age < 65 | ||||||||
| Reference variable (retage normal) = 1 if retirement age >= 65 | ||||||||
| retage 62 only = 1 if retirement age < 63 | ||||||||
| Reference variable (retage 63+) = 1 if retirement age >= 63 | ||||||||
Interaction Effects
The mortality estimates in this paper benefit from the relatively large sample size and number of death observations in the 1973 CPS and suffer from the possibility that the mortality experience of older birth cohorts in the sample differs from that of the younger birth cohorts. Interaction effects are tested to see whether mortality differentials shrink with age and whether the magnitude of the mortality estimates is affected by birth cohort with respect to education and age of retirement. Results indicate that differentials tend to shrink with age. Birth-cohort-interaction effects are found only for the education variables.
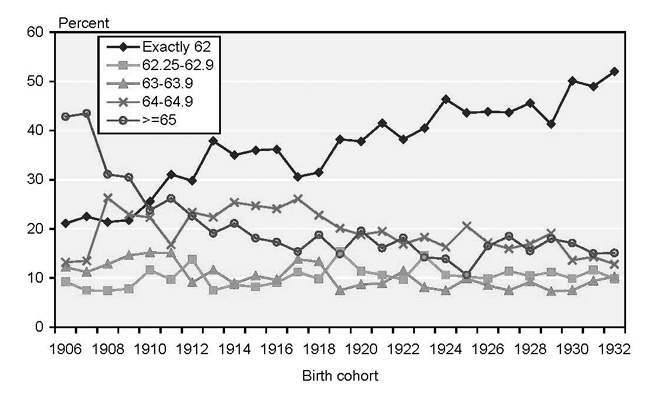
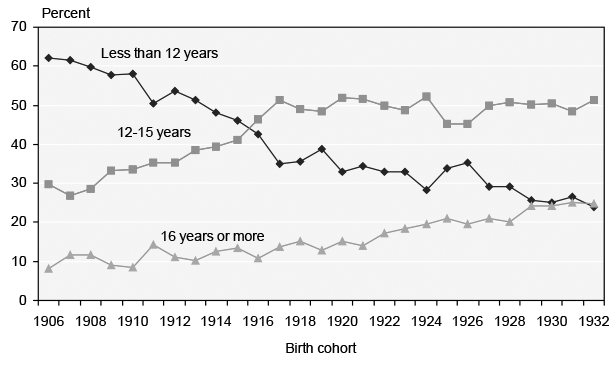
The oldest birth cohort in the sample turns age 62 in 1968, and the youngest birth cohort turns age 62 in 1994. Over this time, the percentage of retirees in a cohort taking benefits at exactly age 62 increases from 21 percent to 52 percent, as shown in Chart 1.19
Percentage of retired male beneficiaries in each birth cohort receiving benefits at each retirement age
| Birth cohort | Retirement age | ||||
|---|---|---|---|---|---|
| Exactly 62 | 62.5–62.9 | 63–63.9 | 64–64.9 | >=65 | |
| 1906 | 21.1 | 9.2 | 12.2 | 13.2 | 42.8 |
| 1907 | 22.5 | 7.5 | 11.2 | 13.5 | 43.5 |
| 1908 | 21.4 | 7.4 | 12.8 | 26.3 | 31.1 |
| 1909 | 21.8 | 7.8 | 14.6 | 22.9 | 30.5 |
| 1910 | 25.6 | 11.6 | 15.2 | 22.3 | 23.8 |
| 1911 | 31.1 | 9.7 | 15.1 | 16.8 | 26.2 |
| 1912 | 29.8 | 13.8 | 9.1 | 23.4 | 22.6 |
| 1913 | 37.9 | 7.5 | 11.6 | 22.4 | 19.1 |
| 1914 | 35.0 | 8.6 | 8.9 | 25.4 | 21.1 |
| 1915 | 36.0 | 8.2 | 10.4 | 24.7 | 18.1 |
| 1916 | 36.2 | 9.1 | 9.6 | 24.1 | 17.3 |
| 1917 | 30.6 | 11.2 | 13.8 | 26.1 | 15.4 |
| 1918 | 31.5 | 9.8 | 13.3 | 22.8 | 18.8 |
| 1919 | 38.2 | 15.4 | 7.5 | 20.1 | 14.9 |
| 1920 | 37.8 | 11.4 | 8.7 | 18.8 | 19.6 |
| 1921 | 41.5 | 10.6 | 8.9 | 19.5 | 16.1 |
| 1922 | 38.2 | 9.7 | 11.4 | 16.9 | 18.2 |
| 1923 | 40.5 | 14.5 | 8.1 | 18.3 | 14.2 |
| 1924 | 46.4 | 10.6 | 7.4 | 16.3 | 13.9 |
| 1925 | 43.6 | 10.3 | 9.9 | 20.6 | 10.6 |
| 1926 | 43.8 | 9.9 | 8.5 | 17.2 | 16.5 |
| 1927 | 43.7 | 11.4 | 7.5 | 16.0 | 18.5 |
| 1928 | 45.6 | 10.4 | 9.2 | 17.0 | 15.5 |
| 1929 | 41.3 | 11.2 | 7.3 | 19.1 | 18.0 |
| 1930 | 50.1 | 9.9 | 7.5 | 13.6 | 17.1 |
| 1931 | 49.0 | 11.6 | 9.4 | 14.3 | 15.0 |
| 1932 | 52.0 | 9.8 | 10.3 | 12.8 | 15.1 |
It seems possible that the 52 percent of all retirees born in 1932 who take benefits at exactly age 62 are more likely to contain a larger group of healthy individuals than the smaller 22 percent of all retirees born in 1906 who take benefits at exactly age 62. If retirees at age 65 are fairly homogeneous, then as more (healthy) individuals migrate to age-62 retirement, the relative average health of age 62 retirees would increase and the relative average health of age 65 retirees would stay constant. Under this scenario, we would expect retirement-age differentials to be larger for the older cohorts and smaller for the younger cohorts. In an alternative scenario, if age 65 retirees are heterogeneous and the healthier age 65 individuals migrate to age 62, the differentials between the two groups would also shrink over time.20
On the other hand, if retirees at age 65 are heterogeneous and those individuals migrating toward early retirement tend to be relatively less robust than those retiring at age 65 and relatively more robust than those retiring at age 62, the relative average health of age 65 retirees might increase. In this scenario, the relative average health of both age 62 retirees and age 65 retirees would increase, so that the differential between the two groups would remain approximately constant over time.
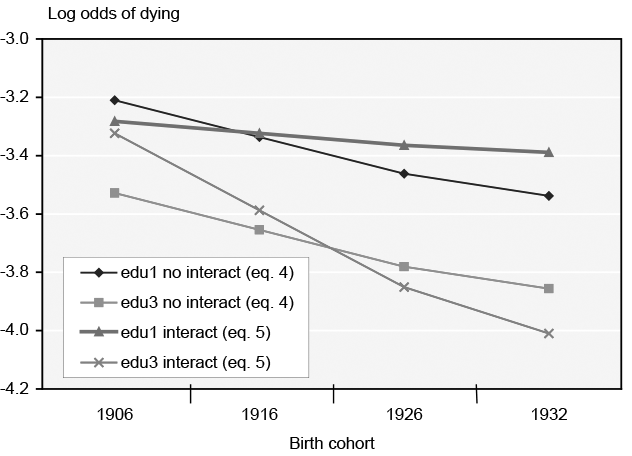
To test for an interaction between year of birth and retirement, I run a regression interacting the four dummy retirement-age variables with year of birth.21 A log likelihood test indicates that the interactions do not add significantly to the explanatory power of equation 4. The dummy variable with the largest movement over time (retage1, or retirement age of exactly 62), when added to the regression equation by itself with a year of birth interaction, also does not add significantly to the explanatory power of equation 4 (at the 5 percent level). However, an interaction of year of birth and retage1 does add to the explanatory power of equation 4 at the 10 percent level. At the 10 percent level, results show the retirement-age differential between exactly age 62 retirees and age 65+ retirees widening over time (see Appendix Chart 1).22 Thus, given my sample size, I do not find evidence to support a hypothesis of a shrinking retirement-age differential over the birth cohorts. Results are more supportive of an approximately constant retirement-age differential over time, or perhaps a slight widening of the spread between the earliest and latest retirees over time.
Similarly, the wide range of birth cohorts in the sample implies that shifts in the average level of educational attainment over time may cause the education variables to change in descriptive power over time. As Appendix Chart 2 shows, 62 percent of the 1906 birth cohort has less than 12 years of education, compared with only 24 percent of the 1932 birth cohort. To capture this movement, I run a regression interacting the education dummy variables with year of birth.23 A log likelihood test of these interactions significantly adds to the explanatory power of equation 4. Specifically (in separate log likelihood tests), year of birth*edu1 is significant and year of birth*edu2 is not. Results show that the spread in mortality risk between men with less than 12 years of education and men with 16 or more years of education widens over time in the 1973 Exact Match (see Appendix Chart 3). The inclusion of the interaction between year of birth and the education dummy variables does not affect the parameter estimates on the other variables like retirement age.
Unfortunately, year-of-birth interactions are only a rough way of trying to capture information from variables that exhibit trends over time. Statistical significance of the interaction between education and year of birth could reflect both the changing proportion of individuals in a particular education category and a residual effect of increasing mortality differentials over time. Pappas and others (1993) find that education differentials have widened from 1960 to 1986, controlling for the change in the percentile of the population at each education level.24 My interaction combines these two effects into a single estimate, so that the cause of the widening differential is ambiguous.
It could also be possible that mortality differentials shrink as individuals live further and further past age 65.25 One would expect this effect if, as the less hardy members of the sample die off, those who remain have an immeasurable propensity toward longevity, independent of the explanatory variables (such as genetic factors). If this is the case, as age increases, the differential variables—education, marital status, and retirement age—will become less and less important as predictors of mortality risk.26
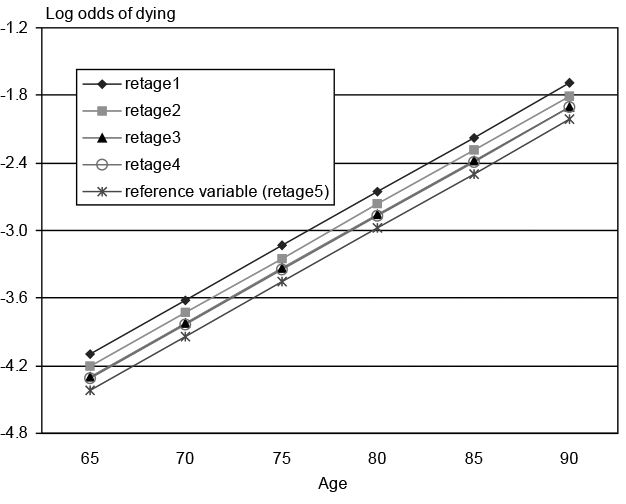
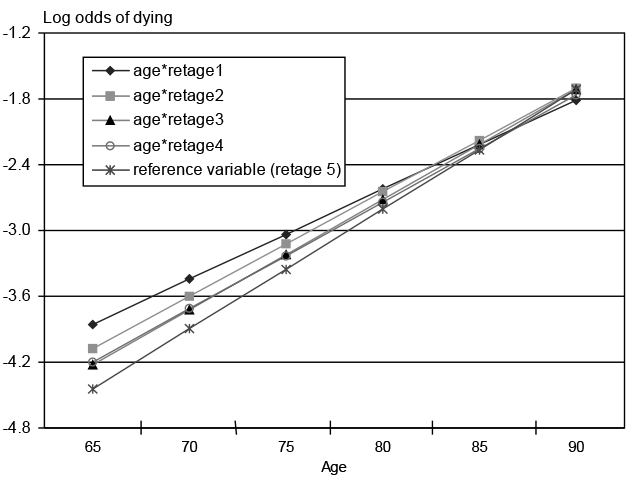
To test for age interaction effects, I run four separate regressions (see Appendix Table 3). Equation 8 interacts age and retirement age, equation 9 interacts age and marital status, equation 10 interacts age and education, and equation 11 interacts age and retirement age, age and marital status, and age and education. When comparing each equation with equation 4 (the regression without interaction effects), each equation has significant log likelihood tests at the 5 percent level, indicating that mortality differentials by retirement age, marital status, and education tend to shrink at older ages. To provide a visual understanding of these results, equations 4 and 8 are depicted in Chart 2. Note that if one compares the two panels, the basic pattern stays the same. Interactions of age*retirement age shrink the differentials at older ages; the rank ordering of these differentials stays pretty much the same. (Crossing at the extreme oldest ages (86–90) may be caused by the small sample size at those ages.)
Mortality risk differentials from age 65 to 90, without and with interaction effects
| Age | retage1 | retage2 | retage3 | retage4 | reference variable (retage5) |
|---|---|---|---|---|---|
| Equation 4: Mortality risk by age of retirement (for married, white, edu2, born in 1926) | |||||
| 65 | -4.0949 | -4.2068 | -4.3007 | -4.3092 | -4.4181 |
| 70 | -3.6144 | -3.7263 | -3.8202 | -3.8287 | -3.9376 |
| 75 | -3.1339 | -3.2458 | -3.3397 | -3.3482 | -3.4571 |
| 80 | -2.6534 | -2.7653 | -2.8592 | -2.8677 | -2.9766 |
| 85 | -2.1729 | -2.2848 | -2.3787 | -2.3872 | -2.4961 |
| 90 | -1.6924 | -1.8043 | -1.8982 | -1.9067 | -2.0156 |
| Equation 8: Age*retirement age interactions (for married, white, edu2, born in 1926) | |||||
| 65 | -3.8541 | -4.0739 | -4.2216 | -4.202 | -4.4452 |
| 70 | -3.4446 | -3.5989 | -3.721 | -3.7145 | -3.8987 |
| 75 | -3.0351 | -3.1239 | -3.2204 | -3.227 | -3.3522 |
| 80 | -2.6256 | -2.6489 | -2.7198 | -2.7395 | -2.8057 |
| 85 | -2.2161 | -2.1739 | -2.2192 | -2.252 | -2.2592 |
| 90 | -1.8066 | -1.6989 | -1.7186 | -1.7645 | -1.7127 |
Conclusion
Evidence from the updated 1973 Exact Match suggests that men retiring early are likely to die sooner than men retiring later. These results persist after controlling for current age, year of birth, education, marital status in 1973, and race. In addition, sample statistics for the 1973 Exact Match show that a greater proportion of age 65 (or older) retirees are college educated than are age 62 retirees. Less-educated male workers who retire early may face higher mortality risk than other groups of workers because of both the correlation between educational attainment and mortality and the correlation between early retirement and mortality. Evaluations of proposals to raise the Social Security retirement age may want to consider such evidence. In addition, evaluations of proposals to index the normal retirement age to improvements in average longevity may want to consider how differing life expectancies could affect the distributional effects of such a proposal.
This study also finds a significant difference in mortality risk for men retiring exactly at age 62 relative to men retiring at age 62 and 3 months to age 62 and 11 months, at age 63, and at age 64. In a heterogeneous population of early retirees, combining age 62 retirees with age 63 and age 64 retirees mutes the higher mortality risk of age 62 retirees. Collapsing retirement-age categories would be of most concern in studies or models focused on changes in the Social Security retirement age—such studies or projections may face the danger of understating effects on a potentially vulnerable subpopulation clustered at exactly age 62. At the least, more research may be needed to address how the complexity of age-of-entitlement patterns affects analyses of "early" retirees.
Finally, mortality estimates such as these benefit from the larger sample size and number of death observations that can be obtained from long panels of longitudinal data. However, because the birth cohorts span 26 years, the mortality experience of older cohorts may not as accurately reflect the present or the future as the mortality experience of more recent birth cohorts. Controlling for year of birth and interacting year of birth with the explanatory variables showing large trends over time is one way to try to adjust for the wide span of birth cohorts in the sample. Although the sample from the updated 1973 Exact Match shows a large trend in the proportion of men retiring at exactly age 62 and in the proportion of men obtaining at least 16 years of education, only the education variables are found to significantly interact with year of birth. The retirement-age differentials estimated in this study appear to be approximately constant over time. Results faintly suggest that the distance in mortality risk between men retiring at exactly age 62 and men retiring at age 65 or older has widened slightly from 1906 to 1932, but these results are significant only at the 10 percent level for the earliest retirement-age coefficient.
Appendix
| Birth cohort | Percentage with given age of retired-worker entitlement | |||||
|---|---|---|---|---|---|---|
| 62 | 63 | 64 | 65 | 65+ | 66+ | |
| 1 Percent Sample of MBR as of June 1998 | ||||||
| 1906 | 27.5 | 12.7 | 17.1 | 40.5 | 42.7 | 2.2 |
| 1907 | 29.6 | 13.7 | 15.5 | 38.8 | 41.2 | 2.4 |
| 1908 | 33.1 | 11.8 | 21.9 | 30.4 | 33.2 | 2.8 |
| 1909 | 34.3 | 15.3 | 19.9 | 28.1 | 30.5 | 2.4 |
| 1910 | 37.3 | 14.6 | 19.7 | 26.0 | 28.4 | 2.4 |
| 1911 | 38.5 | 15.4 | 19.2 | 24.5 | 26.9 | 2.4 |
| 1912 | 42.3 | 15.9 | 17.9 | 21.4 | 23.9 | 2.5 |
| 1913 | 43.7 | 10.8 | 22.2 | 20.6 | 23.3 | 2.7 |
| 1914 | 44.5 | 9.2 | 25.1 | 18.8 | 21.2 | 2.4 |
| 1915 | 43.8 | 10.2 | 25.7 | 17.7 | 20.3 | 2.6 |
| 1916 | 43.5 | 11.4 | 25.0 | 16.2 | 20.1 | 3.9 |
| 1917 | 45.2 | 10.9 | 23.1 | 17.3 | 20.8 | 3.5 |
| 1918 | 47.7 | 10.0 | 21.6 | 17.1 | 20.7 | 3.6 |
| 1919 | 50.2 | 8.8 | 18.5 | 18.5 | 22.5 | 4.0 |
| 1920 | 49.5 | 9.0 | 19.3 | 18.0 | 22.2 | 4.2 |
| 1921 | 51.0 | 8.7 | 18.4 | 17.0 | 21.9 | 4.9 |
| 1922 | 51.8 | 8.6 | 17.9 | 16.3 | 21.7 | 5.4 |
| 1923 | 53.5 | 9.0 | 16.4 | 15.6 | 21.1 | 5.5 |
| 1924 | 53.5 | 8.4 | 15.7 | 16.8 | 22.4 | 5.6 |
| 1925 | 54.4 | 7.9 | 18.9 | 13.8 | 18.8 | 5.0 |
| 1926 | 54.2 | 7.4 | 16.7 | 17.4 | 21.7 | 4.3 |
| 1927 | 54.0 | 8.1 | 16.6 | 16.9 | 21.3 | 4.4 |
| 1928 | 54.6 | 8.7 | 16.5 | 16.3 | 20.2 | 3.9 |
| 1929 | 56.1 | 8.5 | 16.4 | 15.9 | 19.0 | 3.1 |
| 1930 | 57.4 | 8.4 | 15.4 | 16.2 | 18.8 | 2.6 |
| 1931 | 60.0 | 8.1 | 14.6 | 15.6 | 17.3 | 1.7 |
| 1932 | 60.2 | 8.2 | 14.3 | 17.0 | 17.3 | 0.3 |
| 1973 Exact Match (MBR as of approximately June 1998) | ||||||
| 1906 | 30.3 | 12.2 | 13.2 | 42.8 | 44.3 | 1.5 |
| 1907 | 30.0 | 11.2 | 13.5 | 43.5 | 45.3 | 1.8 |
| 1908 | 28.8 | 12.8 | 26.3 | 31.1 | 32.1 | 1.0 |
| 1909 | 29.7 | 14.6 | 22.9 | 30.5 | 32.8 | 2.3 |
| 1910 | 37.2 | 15.2 | 22.3 | 23.8 | 25.3 | 1.5 |
| 1911 | 40.8 | 15.1 | 16.8 | 26.2 | 27.3 | 1.1 |
| 1912 | 43.5 | 9.1 | 23.4 | 22.6 | 24.0 | 1.4 |
| 1913 | 45.4 | 11.6 | 22.4 | 19.1 | 20.6 | 1.5 |
| 1914 | 43.7 | 8.9 | 25.4 | 21.1 | 22.0 | 0.9 |
| 1915 | 44.2 | 10.4 | 24.7 | 18.1 | 20.7 | 2.6 |
| 1916 | 45.2 | 9.6 | 24.1 | 17.3 | 21.1 | 3.8 |
| 1917 | 41.8 | 13.8 | 26.1 | 15.4 | 18.3 | 2.9 |
| 1918 | 41.3 | 13.3 | 22.8 | 18.8 | 22.6 | 3.8 |
| 1919 | 53.6 | 7.5 | 20.1 | 14.9 | 18.8 | 3.9 |
| 1920 | 49.2 | 8.7 | 18.8 | 19.6 | 23.3 | 3.7 |
| 1921 | 52.1 | 8.9 | 19.5 | 16.1 | 19.5 | 3.4 |
| 1922 | 47.9 | 11.4 | 16.9 | 18.2 | 23.8 | 5.6 |
| 1923 | 55.0 | 8.1 | 18.3 | 14.2 | 18.6 | 4.4 |
| 1924 | 57.1 | 7.4 | 16.3 | 13.9 | 19.2 | 5.3 |
| 1925 | 53.9 | 9.9 | 20.6 | 10.6 | 15.6 | 5.0 |
| 1926 | 53.7 | 8.5 | 17.2 | 16.5 | 20.6 | 4.1 |
| 1927 | 55.1 | 7.5 | 16.0 | 18.5 | 21.4 | 2.9 |
| 1928 | 56.1 | 9.2 | 17.0 | 15.5 | 17.7 | 2.2 |
| 1929 | 52.5 | 7.3 | 19.1 | 18.0 | 21.1 | 3.1 |
| 1930 | 60.0 | 7.5 | 13.6 | 17.1 | 18.9 | 1.8 |
| 1931 | 60.6 | 9.4 | 14.3 | 15.0 | 15.7 | 0.7 |
| 1932 | 61.8 | 10.3 | 12.8 | 15.1 | n.a. | n.a. |
| SOURCE: 1973 Exact Match and 1 Percent Sample of the Master Beneficiary Records. | ||||||
| NOTE: n.a. = not applicable. | ||||||
| Variable | Equation 5 | Equation 6 | Equation 7 |
|---|---|---|---|
| Intercept | 40.2178 (14.4039)* |
21.8507 (10.9053)* |
20.7117 (7.1492)* |
| Age | 0.0959 (0.00291)* |
0.0961 (0.00291)* |
0.0961 (0.00291)* |
| Year of birth | -0.0264 (0.0075)* |
-0.0168 (0.00567)* |
-0.0162 (0.00037)* |
| Edu1 | -42.4629 (15.7236)* |
0.3167 (0.00567)* |
0.3165 (0.0533)* |
| Edu2 | -14.836 (16.0717) |
0.1625 (0.0535)* |
0.1635 (0.0535)* |
| Married in 1973 | -0.2624 (0.0452)* |
-0.2599 (0.0452)* |
-0.2593 (0.0452)* |
| African American | 0.1492 (0.0629)* |
0.1538 (0.0629)* |
0.1568 (0.0629)* |
| Retage1 | 0.3269 (0.0429)* |
-19.049 (13.1248) |
-17.8758 (10.2232)** |
| Retage2 | 0.2164 (0.0587)* |
-24.3022 (18.3293) |
0.2203 (0.0588)* |
| Retage3 | 0.1249 (0.0568)* |
-2.9955 (18.7217) |
0.1207 (0.0585)* |
| Retage4 | 0.1121 (0.0476)* |
13.0617 (15.9473) |
0.1155 (0.0477)* |
| Year of birth*Edu1 | 0.0223 (0.00821)* |
n.a. | n.a. |
| Year of birth*Edu2 | 0.00783 (0.00839) |
n.a. | n.a. |
| Year of birth*retage1 | n.a. | 0.0101 (0.00686) |
0.00951 (0.0053)** |
| Year of birth*retage2 | n.a. | 0.0128 (0.00958) |
n.a. |
| Year of birth*retage3 | n.a. | 0.00163 (0.00979) |
n.a. |
| Year of birth*retage4 | n.a. | -0.00676 (0.00834) |
n.a. |
| -2Log likelihood | 35515.121*** | 35519.056 | 35522.824 |
| Latent R 2 | 0.0979587 | 0.0961082 | 0.0954876 |
| SOURCE: Author's calculations on the 1973 Exact Match. | |||
| NOTES: n.a. = not applicable. | |||
| * = standard error significant at the 5 percent level; | |||
| ** = standard error significant at the 10 percent level; | |||
| *** = log likelihood significantly different from equation 4. | |||
| Variable | Equation 8 | Equation 9 | Equation 10 | Equation 11 |
|---|---|---|---|---|
| Intercept | 14.1593 (5.9487)* |
14.444 (5.9419)* |
11.111 (6.0123)** |
12.864 (6.0341)* |
| Age | 0.1093 (0.00504)* |
0.0796 (0.00692)* |
0.1139 (0.00776)* |
0.1064 (0.0105)* |
| Year of birth | -0.0133 (0.00305)* |
-0.0123 (0.00305)* |
-0.0119 (0.00306)* |
-0.0125 (0.00307)* |
| Edu1 | 0.3167 (0.0533)* |
0.3191 (0.0533)* |
1.9775 (0.6258)* |
1.5854 (0.6326)* |
| Edu2 | 0.1635 (0.0535)* |
0.1658 (0.0535)* |
1.3456 (0.6458)* |
1.1081 (0.6469)** |
| Married in 1973 | -0.2567 (0.0452)* |
-1.6909 (0.5477)* |
-0.2598 (0.0452)* |
-1.5486 (0.5447)* |
| African American | 0.1599 (0.0629)* |
0.1538 (0.0629)* |
0.153 (0.0629)* |
0.1551 (0.0629)* |
| Retage1 | 2.3721 (0.5016)* |
0.3223 (0.0428)* |
0.3243 (0.0429)* |
2.1524 (0.5088)* |
| Retage2 | 1.3008 (0.7109)* |
0.2112 (0.0586)* |
0.2113 (0.0586)* |
1.1278 (0.7162) |
| Retage3 | 0.8203 (0.679) |
0.1189 (0.0567)* |
0.1208 (0.0568)* |
0.5886 (0.6853) |
| Retage4 | 1.0102 (0.5741)** |
0.1085 (0.0476)* |
0.1112 (0.0476)* |
0.9003 (0.5773) |
| Age*retage1 | -0.0274 (0.00667)* |
n.a. | n.a. | -0.0245 (0.00677)* |
| Age*retage2 | -0.0143 (0.00947) |
n.a. | n.a. | -0.012 (0.00955) |
| Age*retage3 | -0.00918 (0.00896) |
n.a. | n.a. | -0.00607 (0.00905) |
| Age*retage4 | -0.0118 (0.00759) |
n.a. | n.a. | -0.0104 (0.00763) |
| Age*married in 1973 | n.a. | 0.0193 (0.00733)* |
n.a. | 0.0174 (0.00733)* |
| Age*edu1 | n.a. | n.a. | -0.0222 (0.00833)* |
-0.017 (0.00842)* |
| Age*edu2 | n.a. | n.a. | -0.0158 (0.00863)* |
-0.0127 (0.00864) |
| -2Log likelihood | 35508.484 | 35519.03 | 35518.688 | 35498.33 |
| Latent R 2 | 0.098275 | 0.0963661 | 0.0981843 | 0.102305 |
| SOURCE: Author's calculations on the 1973 Exact Match. | ||||
| NOTES: n.a. = not applicable. | ||||
| * = standard error significant at the 5 percent level; | ||||
| ** = standard error significant at the 10 percent level; | ||||
| Variable | Equation 12 |
|---|---|
| Intercept | 26.8419 (17.5876) |
| Age | 0.1022 (0.0116)* |
| Year of birth | -0.0197 (0.00897)* |
| Edu1 | -26.8235 (19.3456) |
| Edu2 | 2.6364 (19.9337) |
| Married in 1973 | -1.5613 (0.5446)* |
| African American | 0.1509 (0.0629)* |
| Retage1 | 2.1751 (0.5092)* |
| Retage2 | 1.1481 (0.7163) |
| Retage3 | 0.6208 (0.6855) |
| Retage4 | 0.9213 (0.5774) |
| Age*retage1 | -0.0274 (0.00667)* |
| Age*retage2 | -0.0122 (0.00955) |
| Age*retage3 | -0.00643 (0.00905) |
| Age*retage4 | -0.0106 (0.00763) |
| Age*edu1 | -0.00954 (0.0101) |
| Age*edu2 | -0.0126 (0.0105) |
| Age*married in 1973 | 0.0175 (0.00732)* |
| Year of birth*edu1 | 0.0146 (0.00988) |
| Year of birth*edu2 | -0.0008 (0.0102) |
| -2Log likelihood | 35491.89 |
| Latent R 2 | 0.103221 |
| SOURCE: Author's calculations on the 1973 Exact Match. | |
| NOTE: * = standard error significant at the 5 percent level. | |
Year of birth*retage1 (for married, white, age 70, edu1, male)
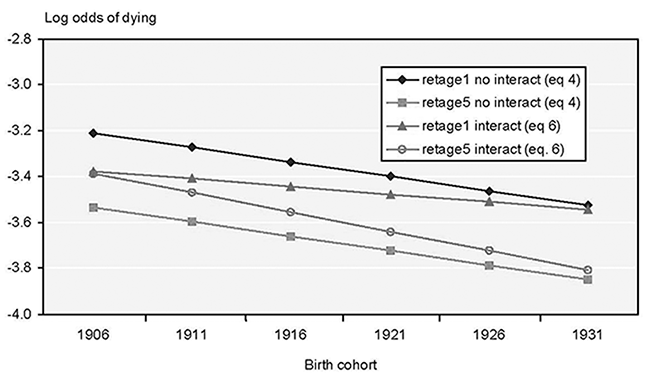
| Birth cohort | No interact (equation 4) | Interact (equation 6) | ||
|---|---|---|---|---|
| retage1 | retage5 | retage1 | retage5 | |
| 1906 | -3.2102 | -3.5334 | -3.3753 | -3.3863 |
| 1911 | -3.2732 | -3.5964 | -3.4093 | -3.4703 |
| 1916 | -3.3362 | -3.6594 | -3.4433 | -3.5543 |
| 1921 | -3.3992 | -3.7224 | -3.4773 | -3.6383 |
| 1926 | -3.4622 | -3.7854 | -3.5113 | -3.7223 |
| 1931 | -3.5252 | -3.8484 | -3.5453 | -3.8063 |
Percentage of birth cohort with given years of education
| Birth cohort | Less than 12 years | 12–15 years | 16 years or more |
|---|---|---|---|
| 1906 | 62.1 | 29.7 | 8.3 |
| 1907 | 61.4 | 26.8 | 11.8 |
| 1908 | 59.7 | 28.6 | 11.7 |
| 1909 | 57.8 | 33.2 | 9.1 |
| 1910 | 58.0 | 33.6 | 8.4 |
| 1911 | 50.4 | 35.3 | 14.3 |
| 1912 | 53.6 | 35.3 | 11.1 |
| 1913 | 51.3 | 38.6 | 10.2 |
| 1914 | 48.0 | 39.5 | 12.6 |
| 1915 | 46.0 | 41.0 | 13.4 |
| 1916 | 42.7 | 46.4 | 10.9 |
| 1917 | 35.0 | 51.4 | 13.7 |
| 1918 | 35.6 | 49.1 | 15.2 |
| 1919 | 38.9 | 48.4 | 12.7 |
| 1920 | 33.1 | 51.8 | 15.2 |
| 1921 | 34.4 | 51.6 | 14.0 |
| 1922 | 33.0 | 49.9 | 17.1 |
| 1923 | 33.1 | 48.6 | 18.3 |
| 1924 | 28.2 | 52.2 | 19.5 |
| 1925 | 33.9 | 45.1 | 21.1 |
| 1926 | 35.4 | 45.1 | 19.5 |
| 1927 | 29.2 | 49.9 | 20.9 |
| 1928 | 29.2 | 50.7 | 20.1 |
| 1929 | 25.7 | 50.1 | 24.2 |
| 1930 | 25.2 | 50.5 | 24.3 |
| 1931 | 26.6 | 48.3 | 25.1 |
| 1932 | 24.0 | 51.4 | 24.7 |
Year of birth*edu (for married, white, age 70, retage1, male)
| Birth cohort | No interact (equation 4) | Interact (equation 5) | ||
|---|---|---|---|---|
| edu1 | edu3 | edu1 | edu3 | |
| 1906 | -3.2102 | -3.5284 | -3.2822 | -3.3231 |
| 1916 | -3.3362 | -3.6544 | -3.3232 | -3.5871 |
| 1926 | -3.4622 | -3.7804 | -3.3642 | -3.8511 |
| 1932 | -3.5378 | -3.856 | -3.3888 | -4.0095 |
Notes
1 To conduct this study, I implicitly assume that probability of death (poor health) can lead to an early retirement but that the state of early retirement does not explicitly cause an increase in the probability of death. Those who believe that the state of early retirement could lead to a loss of "the will to live" and therefore hasten death should note that my retirement-age coefficients would be biased under that assumption.
2 This hypothesis depends on the distribution of the age of onset of disabilities.
3 For example, using the Retirement History Study, Burtless (1987, pp. 133–135) finds that at age 62 "the average probability of working full time for a man in good health was 82 percent and the probability of working full time for a man with a health limitation was 63 percent," controlling for education, earnings, and occupation.
4 Medicare-only beneficiaries in the New Beneficiary Survey are workers aged 65 to 71 in 1982 who have not received retired-worker benefits, usually because they have earnings above the earnings-test limit. The health variable used reflects self-reported health about 18–30 months after the worker first received benefits (Packard 1985, p. 5).
5 Burkhauser, Couch, and Phillips (1996, p. 794, Table 4) and calculations by the author based on internal SSA data used to produce tables for the Annual Statistical Supplement, 1999 to the Social Security Bulletin. An SSA note by Olson (1999, p. 53) estimates that because of lags in the SSA entitlement process, "15 percent of the 1931 [HRS] cohort and 57 percent of the 1932 [HRS] cohort were not "62 enough" in their 62nd birthday years (1993 and 1994, respectively) for their status in their first month of possible benefit receipt to be known." This means that workers may have chosen to take benefits at age 62 but had not received them by the time of the HRS interview (in which case, they would not be included in Burkhauser, Couch, and Phillips’s sample of workers who take benefits at age 62 but instead would be classified as "postponers"). Also, Burkhauser and colleagues were unable to remove noninsured persons from their data, so that some workers classified as "postponers" may have been ineligible for benefits.
6 I have been unable to find a study conducted on a data set contemporary to the HRS that is directly comparable with Burkhauser, Couch, and Phillips. Although researchers have used the 1990s Survey of Income and Program Participation (SIPP) for retirement analysis (for example, Smith 1999), I have not found a study that makes a comparison between early and late retired-worker beneficiaries on health characteristics. Uccello (1998) conducts tabulations on the 1990 SIPP, but her findings are not directly comparable because she does not exclude disabled beneficiaries from her sample and defines retirees as men who are not working, not men who are taking Social Security benefits. However, she does write (p. iv), "… comparisons by health status in this study reveal that retirees are in poorer health than workers of the same age and are more likely to have a condition that limits or prevents work."
7 Author’s calculations of percentages based on sample counts obtained from Leonesio, Vaughan, and Wixon (2000) for Table 3, p. 8. Their paper does not break the data in Table 3 by sex.
8 For this logic to hold, there must not be enough age 62 retirees in above-average health to counter the below-average health of "quasi-disabled" age 62 retirees. My results suggest that among men taking retired-worker benefits at age 62, age 62 retirees in poor health seem to be overwhelming any age 62 retirees in above-average health.
9 In Wolfson and others (1993), the sample was restricted to men who were age 65 on or after September 1, 1979, and they were observed until September 30, 1988.
10 This study uses death data from all three files, in part to account for changes in administrative death reporting over time. (See Aziz and Buckler (1992) for a discussion of death reporting in Social Security administrative records.) The Numident excludes state death data from restricted states. Credit should be attributed to Bert Kestenbaum of SSA/OCACT for having the foresight to do an update of the 1973 Exact Match, without which this analysis would not be possible.
11 Restricting the sample to beneficiaries who attained age 65 eliminates individuals who planned to take benefits at the normal retirement age or later but who died first. Thus, mortality estimates reported in the paper are for male Social Security retired-worker beneficiaries, not male Social Security-covered workers.
12 Birth cohort 1932 is the youngest cohort used because beneficiaries must have attained age 65 by December 31, 1997. At press, I discovered a technical error. Birth cohort 1908 (not 1906) should be the oldest cohort used. Beneficiaries in birth cohorts 1906 and 1907 may be selectively healthier than beneficiaries in other birth cohorts because they have already lived to age 66 or 67 at the time of interview. Luckily, because of the large sample and wide range of birth cohorts, sensitivity tests indicate that the results do not change substantially with this sample correction.
13 One limitation of the historical longitudinal earnings data of Social Security is that earnings are only recorded up to the maximum taxable wage subject to FICA deductions. From 1951 to the mid-1970s, the maximum taxable wage was often close to the average wage. Therefore, information on earnings over the average wage is limited for most of the birth cohorts in the sample. Future work with an earnings variable requires imputation of earnings above the taxable maximum. In addition, the possibility that years of zero earnings represent periods of employment in noncovered work (such as federal, state, and local government) would have to be addressed for this sample.
14 When unstructured standard errors are estimated using a generalized estimating equation (GEE) model (as a test of robustness), standard errors differ only slightly from the conventional logit errors and the significance of the coefficients does not change. All standard errors reported in this paper are produced by the conventional logit model, not the more computationally difficult GEE model. Specifically, equation 4 was estimated using the GEE model to compare the GEE standard errors with the logit standard errors. I was unable to estimate equation 12 using the GEE model, perhaps because of the high degree of multicollinearity induced by the nine interactions in the equation.
15 In this context, the term "life-table method" does not refer to the use of published actuarial tables. Estimates of survival functions are constructed from the 1973 Exact Match sample data using single-year age intervals. The estimates represent the probability that the individual deaths observed in the sample occur at age 80 or later. Censoring is taken into account. See Allison (1995) for details.
16 As will be discussed later, the frequency distribution of education by year of birth changes from 1906 to 1932. However, tabulations made by grouping the birth cohorts into 5-year intervals found the same pattern—a greater proportion of college-educated men retiring at age 65 or older than at exactly age 62 and a lesser proportion of men with less than a high school education retiring at age 65 or older than at the earliest age.
17 If q is the probability of dying, the odds of dying is the ratio of the probability of dying over the probability of not dying (q/1−q. The log odds of dying = 1n(q/1-q).
18 To interpret the odds ratios of the dummy variables (edu1, edu2, married, African American, and retage1 through retage4), one must know the reference variables, which are defined in the note in Table 4. For example, since the reference variable for education is edu3 (16 or more years of education), an odds ratio of 1.375 for edu1 (less than 12 years of education)—in equation 4 means that having less than 12 years of education increases the odds of dying by 38 percent relative to having 16 or more years of education.
19 See Appendix Table 1 for a benchmark of age of retired-worker entitlement by birth cohort in the 1973 Exact Match vs. age of retired-worker entitlement by birth cohort in a 1 percent sample of the Master Beneficiary Records of the Social Security Administration. Since the 1932 cohort in the 1973 Exact Match was age 65 in 1997 and the administrative records for the Exact Match are cut off in March 1998, the 1932 cohort in the Exact Match misses male beneficiaries taking benefits from age 66 or older. In addition, the 1931 cohort in the 1973 Exact Match misses some beneficiaries taking benefits at age 67 or older. However, because of the small percentage of beneficiaries taking benefits past age 65 (1.7 percent for the 1931 cohort in the MBR), I believe this slippage is not a problem.
20 This scenario might describe a situation in which above-average healthy individuals of high socioeconomic status purchase leisure and retire at age 62, as real incomes rise over time. Note that this type of income effect would have to battle a potential substitution effect in the data, where the increase in the real wage for highly educated individuals could raise the price of leisure, discouraging early retirement.
21 See Appendix Table 2, equations 6 and 7, for regression results.
22 In charts in this paper where the values on the y-axis represent the log odds of dying, a greater negative value corresponds to a lower mortality risk. This is a function of the signs on the individual coefficients. With a positive intercept, as age increases, the log odds increase; as year of birth increases, the log odds decrease; being in the edu1 or edu2 category increases the log odds; being married decreases the log odds; being African American increases the log odds; and being in the retage1, retage2, retage3, or retage4 category increases the log odds. Mathematically, in equation 4 where the reference variables all equal zero, y = 13.6958 + 0.0961(65) + −0.126(1906) = −4. Positive coefficients on the reference variables will increase this number, and negative coefficients will decrease it. Thus, being married (−0.2588) decreases the log odds from −4 to −4.2588, and being in categories edu1, edu2, retage1, retage2, retage3, or retage4, increases the log odds (from −4 to −3.3586 for edu1 and retage1).
23 See Appendix Table 2, equation 5, for regression results on education interactions. Tests not reported in this paper showed that when the lowest education dummy variable was split into two dummy variables—less than 9 years of school versus 9–11 years of school—they were not significantly different from each other, although each was individually significant at the 5 percent level versus the reference variable (16 years of school or more). A log likelihood test of the regression with the four education dummies versus the regression with three education dummies was not significant. However, it is a judgment call whether to use more detailed education dummies. I choose not to use greater detail to try to keep the regression as simple as possible.
24 Pappas and others (1993) construct an index to control for changes in educational attainment over the cohorts. Mortality rates from the 1960 Matched Records Survey are compared with rates from the 1986 National Mortality Followback Survey and the 1986 National Health Interview Survey.
25 The idea of age interactions was proposed to me by David Pattison, SSA, and developed by him for an unpublished work.
26 An interaction of age*African American was found insignificant at the 5 percent level. However, other studies have found race differentials crossing at older ages.
References
Allison, Paul D. 1995. Survival Analysis Using the SAS System: A Practical Guide. Cary, N.C.: SAS Institute.
Aziz, Faye, and Warren Buckler. 1992. The Status of Death Information in Social Security Administration Files. Prepared for presentation at the 1992 Joint Statistical Association, Boston, Mass., August 9–13 (unpublished).
Bazzoli, Gloria J. 1985. "The Early Retirement Decision: New Empirical Evidence on the Influence of Health." Journal of Human Resources 20(2): 214–234.
Burkhauser, Richard V.; Kenneth A. Couch; and John W. Phillips. 1996. "Who Takes Early Social Security Benefits? The Economic and Health Characteristics of Early Beneficiaries." The Gerontologist 36(6): 789–799.
Burtless, Gary. 1987. "Occupational Effects on Work and Health Capacity." Work, Health, and Income Among the Elderly. Washington, D.C.: Brookings Institution, pp. 133–135.
Hurd, Michael D., and Kathleen McGarry. 1995. "Evaluation of the Subjective Probabilities of Survival in the Health and Retirement Study." Journal of Human Resources 30:S268–S292.
———. 1997. The Predictive Validity of Subjective Probabilities of Survival. NBER Working Paper No. 6193. Cambridge, Mass.: National Bureau of Economic Research. September.
Kingson, Eric R. 1982. "The Health of Very Early Retirees." Social Security Bulletin 45(9): 3–9.
Leonesio, Michael V.; Denton R.Vaughan; and Bernard Wixon. 2000. Early Retirees Under Social Security: Health Status and Economic Resources. ORES Working Paper No. 86. Social Security Administration, Office of Policy, Office of Research, Evaluation, and Statistics. August.
Olson, Janice A. 1999. "Who is "62 Enough"? Identifying Respondents Eligible for Social Security Early Retirement Benefits in the Health and Retirement Survey." Social Security Bulletin 62(3): 51–56.
Packard, Michael. 1985. "Health Status of New Retired-Worker Beneficiaries: Findings from the New Beneficiary Survey." Social Security Bulletin 48(2): 5–16.
Pappas, Gregory; Susan Queen; Wilbur Hadden; and Gail Fisher. 1993. "The Increasing Disparity in Mortality Between Socioeconomic Groups in the United States, 1960 and 1986." New England Journal of Medicine 329(2): 103–109.
Sammartino, Frank J. 1987. "The Effect of Health on Retirement." Social Security Bulletin 50(2): 31–47.
Smith, Ralph. 1999. Raising the Earliest Eligibility Age for Social Security Benefits. Washington, D.C.: Congressional Budget Office.
Social Security Administration, Office of Policy, Office of Research and Statistics, Program Analysis Staff. 1982. "Mortality and Early Retirement." Social Security Bulletin 45(12): 3–10.
Uccello, Cori E. 1998. Factors Influencing Retirement: Their Implications for Raising the Retirement Age. No. 9810. Washington, D.C.: Public Policy Institute, American Association of Retired Persons. October.
Wolfson, Michael; Geoff Rowe; Jane F. Gentleman; and Monica Tomiak. 1993. "Career Earnings and Death: A Longitudinal Analysis of Older Canadian Men." Journal of Gerontology 48(4): S167–S179.