How Do Trends in Women's Labor Force Activity and Marriage Patterns Affect Social Security Replacement Rates?
Social Security Bulletin, Vol. 73, No. 4, 2013 (released November 2013)
This article examines how women's increased labor force participation, increased earnings, and reduced marriage rates affect Social Security replacement rates over time. Based on data from the Health and Retirement Study and Modeling Income in the Near Term, our estimates show that Social Security replacement rates have dropped sharply at both the household and individual levels, and the declines will continue for future retirees. We also find that this aggregate change masks a complex relationship between replacement rates and the marital status and income levels of individuals. The decline in replacement rates over time is largest for married couples with husbands having higher earnings. Increases in the labor force activity and earnings of women explain more than one-third of the change. By contrast, the impact of changing marital patterns is relatively small. Changes to the full retirement age and the timing of benefit claiming explain much of the remaining decline.
April Yanyuan Wu is a research economist with the Center for Retirement Research (CRR) at Boston College. Nadia Karamcheva is a research associate with the Urban Institute. Alicia Munnell is the Peter F. Drucker Professor of Management Sciences at Boston College's Carroll School of Management and the director of the CRR at Boston College. Patrick Purcell is an economist with the Office of Policy Evaluation and Modeling, Office of Research, Evaluation, and Statistics, Office of Retirement and Disability Policy, Social Security Administration.
Acknowledgments: The authors thank Zhenya Karamcheva, Katherine Burnham, and Madeline Medenica for excellent research assistance. The authors also thank Ben Bridges, Barbara A. Butrica, Irena Dushi, Melissa Favreault, Susan Grad, Alice M. Henriques, Virginia P. Reno, Karen E. Smith, Glenn Springstead, and Karen van der Wiel for their thoughtful comments and suggestions.
Contents of this publication are not copyrighted; any items may be reprinted, but citation of the Social Security Bulletin as the source is requested. The findings and conclusions presented in the Bulletin are those of the authors and do not necessarily represent the views of the Social Security Administration, the CRR at Boston College, or the Urban Institute.
Introduction
| AIME | average indexed monthly earnings |
| DE | Depression Era |
| EBB | early baby boomer |
| FRA | full retirement age |
| Gen X | generation X |
| HRS | Health and Retirement Study |
| LBB | late baby boomer |
| MBB | middle baby boomer |
| MINT | Modeling Income in the Near Term |
| PIA | primary insurance amount |
| SIPP | Survey of Income and Program Participation |
| SSA | Social Security Administration |
For the medium earner, the percentage of preretirement earnings replaced by Social Security benefits—the replacement rate—rose from about 30 percent in the 1970s to 40 percent in the 1980s, where it remains today (Board of Trustees 2012). Replacement rates for individuals and households depend partly on Social Security program provisions and partly on retirees' labor force histories and household arrangements.
Although an extensive literature has explored how policy changes affect the Social Security program, only a few studies have focused on the impacts of demographic factors—importantly, the changing role of women.1 Compared with 30 years ago, women today have higher levels of education, increased labor force participation, more stable career trajectories, higher salaries, and a higher probability of being divorced or never married.
This article explores how the changing trends among women affect Social Security replacement rates and thereby the program's finances. The analysis starts with trends in replacement rates for current retirees based on data from the Health and Retirement Study (HRS), which contains workers' actual lifetime earnings profiles as well as their demographics, including marital status. We then use the Modeling Income in the Near Term (MINT) microsimulation model to project changes in replacement rates for future retirees. The article extends previous studies in that it makes use of these rich data sources to calculate replacement rates across a broad range of birth cohorts: Depression Era 1 (DE1, born 1931–1935), Depression Era 2 (DE2, born 1936–1941), war baby (born 1942–1947), early baby boomer (EBB, born 1948–1953), middle baby boomer (MBB, born 1954–1959), late baby boomer (LBB, born 1960–1965), and generation X (Gen X, born 1966–1975). Moreover, information on actual workers makes it possible to examine changes in replacement rates within cohorts by marital status and by income.
The article also uses an Oaxaca-Blinder method to decompose the replacement rate changes into contributing factors such as labor force activity; marital patterns; and the timing with which Social Security benefits are claimed, against the backdrop of the legislated gradual increase of the full retirement age (FRA). This approach not only isolates the impact of the changing trends among women from other factors, it also allows us to quantify the effect of these sweeping changes on replacement rates over time.
This article focuses on replacement rates—benefits as a percentage of preretirement earnings. As wages have risen over time, so have Social Security benefit levels; therefore, relative measures, such as replacement rates, are more appropriate than absolute measures when assessing the degree to which the program helps beneficiaries maintain their standard of living in retirement. Of course, Social Security is only one component of retirement income, and therefore Social Security replacement rates alone do not provide a complete measure of retirement income adequacy; however, because Social Security is the largest source of retirement income for a majority of retirees, the replacement rate is nevertheless an important measure.
The article is arranged in six sections, beginning with this introduction. The second section provides background information on the Social Security program, documents how women's roles have changed over time, and presents a brief overview of prior studies. The third section describes the data sets and the methodology. The fourth section summarizes the trends in replacement rates across cohorts and within cohorts by marital status and income. The fifth section discusses the decomposition procedure used to investigate how the changing roles of women—characterized by both labor force activity and marital patterns—explain the differences in replacement rates across cohorts. The final section concludes.
The findings can be summarized as follows. First, the changing role of women has led to a marked decrease in the proportion of preretirement income that Social Security replaces at both the household and individual levels, and the decline will continue for future retirees. Second, changes at the aggregate level mask the more complex relationship by marital status. The change is relatively modest for the never-married, but is larger for married, divorced, and widowed households. The decline in replacement rates for couples is largest for households with husbands' earnings in the top tercile. At the individual level, the decline in replacement rates is most dramatic for widows, and the decline is more pronounced for women than for men.
Third, the decomposition analysis shows that changes in labor force participation, including increased labor supply and earnings, account for more than one-third of the difference in replacement rates between individuals born 1931–1935 and those born 1966–1975. Although marital patterns have also changed dramatically over time, the impact of that factor is relatively small. However, changes to the FRA and in claiming behaviors across cohorts explain a significant fraction of the change in replacement rates. Nevertheless, up to 30 percent of the change across cohorts cannot be attributed to differences in mean characteristics identified in our analysis, and remain “unexplained.” Those unexplained differences could be driven in part by the underlying assumptions used for the projection, as the explanatory power of the models is significantly higher for comparisons of cohorts who have already claimed Social Security benefits or will do so in the near future. As the age difference between cohorts grows, the explanatory power of the models declines.2
Background
This section frames the trends and parameters our study examines. It addresses the Social Security program characteristics relevant to retired-worker benefits, long-term changes in economic and marital patterns among women, and existing literature on those topics.
Social Security Program
Before exploring how women's labor force activity affects replacement rates, it is necessary to understand how Social Security benefits are determined. Social Security benefits, on which over one-third of beneficiaries aged 65 or older depend for 90 percent or more of their total income, are programmatically linked to both earnings and marital histories (SSA 2012). Social Security pays retired-worker benefits to individuals who have accumulated 40 or more quarters of earnings in covered employment over their lives. Benefits at FRA are determined with a three-step process. First, a worker's previous earnings are restated in terms of current wages by indexing past earnings (up to age 60) to wage growth. Second, indexed earnings for the highest 35 earnings years are averaged and then divided by 12 to determine average indexed monthly earnings (AIME). The final step is to calculate the primary insurance amount (PIA), which equals the sum of different percentages of three separate portions of the AIME. The portions are determined by a formula that uses earnings thresholds—or “bend points”—that are indexed to wage growth, and thus depend on the year in which a person reaches age 62. For example, the PIA for workers first becoming eligible for benefits in 2013 is calculated as follows:
- 90 percent of the first $791 of their AIME plus
- 32 percent of AIME between $791 and $4,768 plus
- 15 percent of any AIME in excess of $4,768.
The benefit actually paid depends on when the worker claims. Benefits paid between age 62 and the FRA are actuarially reduced, and benefits paid between the FRA and age 70 are actuarially increased.
In addition to the worker's own benefit, Social Security provides dependent (or “auxiliary”) benefits to qualified spouses of retired workers. Although those benefits are not gender-based, they typically go to women because women have historically tended to work and earn less than men. Thus, a wife is entitled to either of two types of benefits: (1) a spouse's benefit that bridges any gap between her own retirement benefit and 50 percent of her husband's PIA (unreduced for his early retirement); or (2) a survivor's benefit that bridges any gap between her own benefit and 100 percent of her husband's benefit (reduced for early retirement). Divorced spouses are entitled to dependent benefits if their marriage lasted at least 10 years.
When most people retired as married couples and most women did not work, it was straightforward to calculate replacement rates. The wife who claimed benefits at her FRA was entitled to a benefit equal to 50 percent of her husband's (if he also claimed at FRA), so if the replacement rate for the typical worker was 40 percent, the replacement rate for the couple would be 60 percent. As women increasingly joined the workforce, the calculation became less obvious, because married women were entitled to the larger of either the spouse's benefit or the benefit they could earn on their own. Further, over time, the share of never-married or ever-divorced women reaching retirement has increased and will continue to rise.
Women's Changing Economic and Social Characteristics
On virtually every dimension, women's economic and social characteristics have changed, and these changes are remaking the current and future profile of the US retiree population. This subsection describes the changing role of women in two key dimensions: labor force participation and marital status.
Labor market trends. Women's labor force participation has risen dramatically over the past five decades. Only 37 percent of women aged 20–64 worked in 1950, but more than 71 percent of them worked by 2011. Chart 1 shows the labor force participation rate of women aged 25–34 by birth cohort. For Gen X women, 73 percent were in the labor force at ages 25–34, about twice the rate for DE1 women.
Labor force participation rates for all and married women aged 25–34, by birth cohort
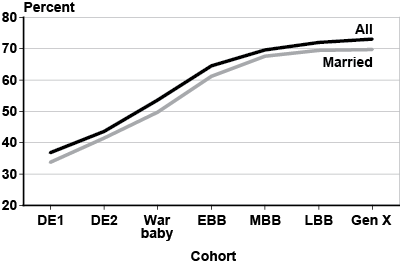
| Cohort | All | Married |
|---|---|---|
| DE1 | 36.73 | 33.63 |
| DE2 | 43.60 | 41.37 |
| War baby | 53.58 | 49.71 |
| EBB | 64.42 | 61.17 |
| MBB | 69.56 | 67.51 |
| LBB | 71.90 | 69.45 |
| Gen X | 72.97 | 69.73 |
The increase in labor force participation has occurred mostly among married women: Between 1970 and 2010, the percentage of married women in the labor market rose from 40 percent to 61 percent (Kreider and Ellis 2011). Similarly, Chart 1 shows that 34 percent of married DE1 women aged 25–34 were in the labor force; the corresponding number for married Gen X women is close to 70 percent.
Participation levels do not tell the whole story. Occupation and pay scale also determine how labor market trends affect the economic status of women. With respect to job type, women are moving away from lower-paying jobs towards managerial and professional positions with higher wages. Currently, 40 percent of women are in managerial and professional jobs, compared with just 18 percent in 1975 (Department of Labor 2010).
The gender difference in wages has endured, but it is declining. Women who work full time are now earning 80 percent of the male wage, compared with 62 percent in 1979 (BLS 2008). Chart 2 shows the median ratio of the wife's AIME to husband's AIME by cohort. Gen X wives are projected to earn about 68 percent of their husbands' lifetime earnings, which is 2.3 times the ratio for DE1 wives. As more women enter the labor force, and their earnings increase relative to their husbands' earnings, more women qualify for worker-only benefits. Similarly, the proportion of women receiving only spousal or widow's benefits will decline over time.
Median ratio of wife's AIME to husband's AIME, by birth cohort
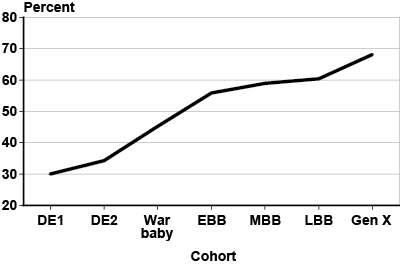
| Cohort | Percent |
|---|---|
| DE1 | 29.89 |
| DE2 | 34.19 |
| War baby | 45.11 |
| EBB | 55.83 |
| MBB | 58.93 |
| LBB | 60.40 |
| Gen X | 68.04 |
Marriage trends. Dramatic changes in family formation have occurred in the past four decades. Two family formation behaviors—marriage and divorce—are critical to determining Social Security outcomes and adequacy.
Marriage rates have fallen sharply over the past few decades. Chart 3 summarizes marriage trends for women by age and cohort. Although 84 percent of DE1 women were married at ages 25–34, the proportion declines to less than 60 percent for Gen Xers. Although nearly 70 percent of women in the oldest cohort were married at ages 55–64, the proportion is projected to decline for Gen Xers to about 56 percent. Along with changing marriage rates, the median age at first marriage has also increased, from 20.3 in 1950 to 25.1 in 2000 (Kreider and Ellis 2011).
Percentage of women who are married, by age group and birth cohort
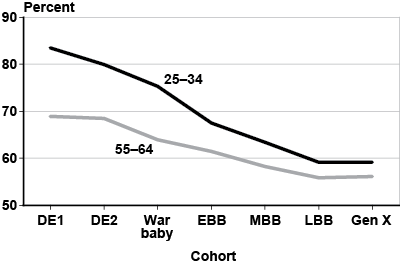
| Cohort | 25–34 | 55–64 |
|---|---|---|
| DE1 | 83.45 | 68.92 |
| DE2 | 79.90 | 68.44 |
| War baby | 75.33 | 63.95 |
| EBB | 67.48 | 61.40 |
| MBB | 63.40 | 58.27 |
| LBB | 59.16 | 55.79 |
| Gen X | 59.10 | 56.14 |
Divorce rates increased rapidly beginning in 1960, peaked in 1979, and have remained flat since the mid-1980s. Although the divorce rate has leveled off, the characteristics of divorce have been changing. In particular, the duration of marriages ending in divorce appears to have declined among more recent cohorts of women. Among first marriages, the share of those who remained married at their 10th anniversaries declined from 82.8 percent for those married in 1960–1964 to 74.5 percent for those married in 1990–1994 (Kreider and Ellis 2011).
As a result of trends in marriage, divorce, and marriage duration, a higher percentage of women is likely to enter retirement without having married or having been married only for a short time, which has important implications for women's retirement security generally and their Social Security benefits specifically.
Literature to Date
Although an extensive literature has explored how policy changes affect the Social Security program, only a few studies have focused on the impact of demographic factors—particularly the changes among women. Using MINT, Butrica, Iams, and Smith (2007) and Butrica, Smith, and Iams (2012) examine how sweeping demographic and economic changes (including rising educational attainment, changing marital patterns, changes in both women's and men's labor force participation and earnings, and the increasing share of immigrants and minorities) impact retirement income across generations. They find that total income replacement rates will decline and that baby boomers and Gen Xers are less likely than current retirees to have enough postretirement income to maintain their preretirement standard of living.
A few studies have focused specifically on women. Butrica and Smith (2012a) explore the impact of women's increasing labor force participation and earnings on married women's Social Security benefits and find that the share of married women projected to receive spouses' benefits at retirement has declined in more recent birth cohorts. Although most wives will still be eligible for survivor benefits, the ineligible share is projected to double between cohorts. Using the Current Population Survey, Munnell, Sanzenbacher, and Soto (2007) evaluate the impact of the increased labor force participation of wives on the Social Security replacement rate for couples and find that, over the past 40 years, the rate for the hypothetical average couple has declined from 50 percent to 45 percent.
Another strand of literature examines changes in marital patterns and the economic well-being of divorced women in retirement. For instance, Butrica and Smith (2012b) find that changes in women's earnings, work patterns, and marriage-duration trends result in more divorced women receiving retired-worker benefits based on their own earnings. However, those who do not meet the 10-year marriage requirement are projected to have low retirement income and high poverty rates.
This article, which builds on the existing literature, has three goals. The first is to investigate how Social Security replacement rates have changed across a broad range of cohorts, and within cohorts by marital status and income. Second, the study aims to improve the estimates of the previous studies by using data from two different household surveys matched with Social Security administrative records. The third goal is to determine the extent to which the changing trends among women can explain the pattern of replacement rates across cohorts.
Data and Methodology
This section begins with a description of the datasets. It then describes the methodology of the replacement rate calculations.
Data
The analysis of current retirees uses data from the HRS 1992 through 2010 waves, matched to Social Security administrative records for covered earnings from 1951 through 2008.3 The HRS is a nationally representative longitudinal study of older Americans. The survey began in 1992 with an initial cohort of 12,652 individuals from 7,607 households in which at least one member was born during 1931–1941. Additional cohorts were added later. Individuals may consent to have their Social Security earnings histories linked to the survey, and approximately 70 percent of respondents have done so. Our HRS sample is grouped into four birth cohorts: DE1 (1931–1935), DE2 (1936–1941), war baby (1942–1947), and EBB (1948–1953).4, 5
To project replacement rates for future retirees, we use MINT, a microsimulation model developed by the Social Security Administration (SSA). MINT links individuals' demographic information, marital histories, and income and wealth information from the Survey of Income and Program Participation (SIPP) with their earnings and benefit histories from Social Security administrative data. Based on those data, MINT projects each retiree's income from Social Security benefits, pensions, assets, and, for working beneficiaries, earnings. Using MINT, we can project the changes in replacement rates for the MBB (1954–1959), LBB (1960–1965), and Gen X (1966–1975) birth cohorts, where female labor force participation and marital patterns have changed most dramatically. MINT can also be used to estimate benefits for households that are already retired.6
Replacement Rate Calculation Methodology
In this study, we define replacement rate as the ratio of the Social Security benefit to the AIME. As discussed in Purcell (2012), there is no common measure of replacement rates. Whether a given replacement rate represents an adequate retirement income depends on whether the denominator in the replacement rate calculation is an appropriate measure of preretirement earnings. We use AIME in the replacement rate calculation rather than peak or final earnings because the AIME measures lifetime earnings and thus reflects available resources over individuals' careers, from which they could reasonably accrue retirement income.
Estimating the replacement rate is a three-step process. First, we construct the lifetime earnings profile; second, we estimate Social Security benefits based on earnings and marital-status histories; and third, we calculate replacement rates at the time of first benefit receipt to account for actuarial adjustments for early or delayed claiming.
Lifetime earnings. Lifetime earnings serve as the base for calculating career average indexed earnings and Social Security benefits. As noted earlier, matched administrative data provide Social Security earnings histories back to 1951 for the approximately 70 percent of the HRS sample that has consented to data linkage. Although previous work has documented that giving permission to link is nonrandom (Haider and Solon 2000), the distribution of Social Security benefits is similar across the linked and nonlinked respondents (Kapteyn and others 2006). Thus, for the approximately 30 percent of the HRS sample that has not consented to link, we follow Gustman and Steinmeier (2001) and estimate earnings histories based on survey data on previous jobs and wages, using the estimated returns to tenure from Anderson, Gustman, and Steinmeier (1999).7
MINT projects each person's mortality, entry to and exit from the Social Security Disability Insurance rolls, and age at first receipt of Social Security retirement benefits. For younger cohorts, MINT projections are adjusted for expected demographic and socioeconomic changes. Further, MINT accounts for the growth of economy-wide real earnings, the distribution of earnings both between and within birth cohorts, and the composition of the retiree population. Because MINT simulates the whole earnings profile, no additional simulation is needed.
Social Security benefits. As discussed in the background section, SSA calculates the PIA by applying a piecewise linear formula to each worker's AIME. In computing AIMEs using HRS data, we follow the SSA practice of indexing earnings prior to age 60 to the average wage index for the year the individual attains age 60.8 Earnings after age 60 are not indexed. AIME is the simple monthly average of the indexed earnings in the 35 highest-earnings years. At FRA, a retiree is entitled to a benefit equal to the PIA. A worker may choose to retire as early as age 62, with reduced benefits. Conversely, if a worker delays receipt of benefits to an age as late as 70, the eventual benefits are permanently increased for each year of delay.
Marital status at retirement and marital history are important in determining spousal or survivor benefits. Those who have claimed Social Security benefits are categorized according to marital status at the time of first benefit receipt. In the HRS data for those not yet retired, we assume that the last reported marital status does not change before retirement. If a respondent is divorced with a previous marriage that lasted 10 or more years, we first determine if the sample includes the ex-spouse. If not, we match the respondent to someone else in the survey by sex, education, race, and 5-year birth-year band. We then use the earnings history of the matched spouse to compute the spousal and survivor benefit available from the ex-spouse. For the widow(er)s whose deceased spouses are missing from the sample, we match the respondent with another widow(er) in the sample, based on sex, race, education, 5-year birth cohort, and retirement age. We then use the earnings history of that person's deceased spouse to estimate survivor benefits.
We use an analogous method to calculate benefits using MINT data. MINT observes marriage patterns in the periods covered in the SIPP panels when husbands and wives can be precisely identified. For individuals projected to change marital status after the last SIPP observation (or whose former spouses from before the SIPP panel are not observed), the model statistically matches married individuals to a spouse with characteristics of a likely match. The spousal and survivor benefits then are calculated using data for the observed and imputed spouses.
Mortality adjustments. In the 2010 HRS, some war baby and EBB respondents had not yet retired, requiring mortality adjustments to account for the possibility of their dying before claiming.9 Mortality assumptions are already imbedded in the MINT data; therefore, no additional adjustments or projections are needed (Smith and others 2010, II-11).
Replacement rates by marital status. For currently married households, the replacement rate is the ratio of household benefits (the sum of the husband's and the wife's benefit) to the sum of each spouse's AIME. It is calculated as of the first time that both spouses receive their Social Security benefits. For individuals who are widowed or divorced when they start receiving benefits, we create a lifetime shared earnings measure that equals the individual's earnings in the years when not married and the average of the couple's earnings in the years when married. Thus, the household replacement rate for widowed and divorced persons is the ratio of the benefit that the widow(er)/divorcee receives to the average lifetime shared indexed earnings. At the individual level, we calculate the replacement rate as the ratio of the benefit (which can be a spouse/survivor or a retired-worker benefit) to the individual's career average indexed earnings.10
Cross-cohort demographic changes. HRS data for the DE1, DE2, war baby, and EBB cohorts suggest several reasons why Social Security replacement rates have changed over time (Table 1). Marriage rates have declined across successive cohorts, and the labor force participation of women has increased (based on Social Security quarters of coverage).11 The share of individuals that are divorced or never married when they first claim has risen from about 29 percent for the DE1 cohort to 44 percent for the EBB cohort. Quarters of coverage have increased dramatically for women, by about 20 percent to 40 percent over time for those who were ever married. That change has increased the share of women eligible for Social Security retired-worker benefits based on their own earnings: Only 50 percent of women were eligible for benefits as a retired worker in the DE1 cohort compared with 73 percent in the EBB cohort.12 At the same time, women eligible only for auxiliary benefits declined from 25 percent in the oldest cohort to about 9 percent in the youngest. Along with the increased female labor market attachment, household AIME rose, with the biggest increase among married couples. Although the benefit amounts have also increased over time, those changes are relatively modest compared with the changes in AIME, suggesting that replacement rates may continue to fall.
| Characteristic | DE1 (1931–1935) | DE2 (1936–1941) | War baby (1942–1947) | EBB (1948–1953) |
|---|---|---|---|---|
| Percentage distributions | ||||
| Sex | ||||
| Men | 46.3 | 47.6 | 47.2 | 46.9 |
| Women | 53.7 | 52.4 | 52.8 | 53.1 |
| Marital status | ||||
| Married | 54.7 | 53.5 | 52.7 | 49.7 |
| Divorced | 22.7 | 29.0 | 31.6 | 35.7 |
| Never married | 5.9 | 6.0 | 6.5 | 8.3 |
| Widowed | 16.7 | 11.5 | 9.2 | 6.3 |
| Education | ||||
| Less than high school | 22.0 | 17.3 | 9.9 | 8.8 |
| High school degree | 57.9 | 58.9 | 60.7 | 56.7 |
| At least some college | 20.1 | 23.8 | 29.5 | 34.5 |
| Benefit type (women only) | ||||
| Retired worker | 50.3 | 56.9 | 64.1 | 72.5 |
| Dually entitled | 25.1 | 26.5 | 23.8 | 18.9 |
| Auxiliary only | 24.7 | 16.6 | 12.1 | 8.6 |
| Cohort average values | ||||
| Quarters of coverage | ||||
| Women | ||||
| Married | 89 | 103 | 113 | 124 |
| Divorced | 109 | 114 | 124 | 133 |
| Never married | 145 | 145 | 143 | 153 |
| Widowed | 98 | 95 | 113 | 117 |
| Men | ||||
| Married | 147 | 156 | 154 | 154 |
| Divorced | 135 | 144 | 152 | 152 |
| Never married | 122 | 139 | 146 | 147 |
| Widowed | 142 | 151 | 141 | 148 |
| AIME (annual, household level, 2012 dollars) | ||||
| Marital status | ||||
| Married | 55,679 | 70,879 | 81,200 | 89,750 |
| Divorced | 24,786 | 30,951 | 36,551 | 39,769 |
| Never married | 25,258 | 37,799 | 38,924 | 43,330 |
| Widowed | 20,774 | 21,630 | 28,142 | 29,229 |
| Benefit amount (annual, household level, 2012 dollars) | ||||
| Marital status | ||||
| Married | 24,783 | 29,071 | 29,736 | 32,271 |
| Divorced | 11,428 | 13,338 | 14,091 | 14,906 |
| Never married | 10,966 | 14,560 | 14,201 | 15,671 |
| Widowed | 11,805 | 13,528 | 15,063 | 16,626 |
| Number of observations | 3,397 | 4,345 | 2,014 | 2,544 |
| SOURCE: Authors' calculations based on the HRS. | ||||
| NOTE: Rounded components of percentage distributions do not necessarily sum to 100.0. | ||||
Changes in Replacement Rates Over Time
This section examines cross-cohort differences in replacement rates. We first examine the cohorts covered in the HRS sample; then, we look at the MINT cohorts.
Current Retirees: Actual Earners in the HRS
Table 2 shows individual replacement rates for the same four cohorts shown in Table 1. The median replacement rate for all groups has declined over time, from 47 percent for the DE1 cohort to 39 percent for the EBB cohort.13 The aggregate trend masks more complex patterns by sex and marital status: The decline is more dramatic for women than for men, and the drop in the replacement rate for women is substantially larger for the currently married, divorced, and widowed than for the never-married. Those patterns reflect the changing labor force participation of married women: As more married women work, more of them earn their own benefits, which reduces their eligibility for spousal benefits and lowers their replacement rate.
| Marital status and sex | DE1 (1931–1935) | DE2 (1936–1941) | War baby (1942–1947) | EBB (1948–1953) |
|---|---|---|---|---|
| All individuals | 47 | 44 | 39 | 39 |
| Men | 38 | 37 | 34 | 35 |
| Women | 65 | 56 | 49 | 45 |
| Never married | ||||
| Men | 50 | 45 | 39 | 41 |
| Women | 43 | 41 | 38 | 42 |
| Currently married | ||||
| Men | 38 | 37 | 33 | 34 |
| Women | 70 | 56 | 49 | 45 |
| Widowed | ||||
| Men | 41 | 37 | 37 | 34 |
| Women | 72 | 82 | 77 | 62 |
| Divorced | ||||
| Men | 40 | 39 | 37 | 36 |
| Women | 57 | 52 | 44 | 42 |
| SOURCE: Authors' calculations based on the HRS. | ||||
| NOTE: "Replacement rate" is defined as the Social Security benefit amount divided by AIME. | ||||
The change in median household replacement rates (Table 3) largely mirrors that for individual replacement rates.14 Among married couples, the results are broken out for single-earner and two-earner households; a single-earner household is one in which only one spouse works long enough to qualify for Social Security worker benefits and a two-earner household is one in which both spouses qualify for benefits based on their own earnings histories.15 The decline for two-earner households is greater than that for single-earner households, reflecting the fact that working wives add substantially more to married couples' preretirement earnings than they do to their Social Security benefits.16
| Marital status | DE1 (1931–1935) | DE2 (1936–1941) | War baby (1942–1947) | EBB (1948–1953) |
|---|---|---|---|---|
| All households | 47 | 44 | 39 | 39 |
| Never married | 49 | 44 | 38 | 42 |
| Currently married | ||||
| Single earner | 54 | 53 | 49 | 52 |
| Two earners | 43 | 41 | 37 | 36 |
| Combined | 46 | 42 | 38 | 37 |
| Widowed | 64 | 68 | 61 | 61 |
| Divorced | 48 | 46 | 40 | 39 |
| SOURCE: Authors' calculations based on the HRS. | ||||
| NOTE: "Replacement rate" is defined as the Social Security benefit amount divided by AIME. | ||||
Table 4 shifts the focus from marital status to earnings and shows replacement rates of married couples by the husband's earnings level. Over time, the replacement rate has declined more for households with husbands in the top earnings tercile than for households with a husband in the bottom earnings tercile, in terms of percent change from the baseline. That pattern likely reflects the change in the correlation between husbands' and wives' earnings. Schwartz (2010) reports that the earnings of husbands and wives were negatively correlated in the late 1960s and 1970s; but as highly educated women increasingly joined the workforce thereafter, the correlation became positive.
| Number of earners and husband's earnings tercile | DE1 (1931–1935) | DE2 (1936–1941) | War baby (1942–1947) | EBB (1948–1953) |
|---|---|---|---|---|
| Single-earner households | ||||
| Low | 67 | 71 | 78 | 76 |
| Median | 51 | 52 | 48 | 51 |
| High | 45 | 46 | 39 | 39 |
| Dual-earner households | ||||
| Low | 52 | 49 | 44 | 45 |
| Median | 42 | 40 | 36 | 36 |
| High | 37 | 35 | 31 | 30 |
| All households | ||||
| Low | 57 | 53 | 47 | 48 |
| Median | 45 | 42 | 38 | 37 |
| High | 38 | 35 | 31 | 30 |
| SOURCE: Authors' calculations based on the HRS. | ||||
| NOTE: "Replacement rate" is defined as the Social Security benefit amount divided by AIME. | ||||
Future Retirees: Projections Using MINT
Although the growth in women's labor force participation has slowed, later cohorts will have increasing shares of women who spend most of their lives in the workforce. Further, the shares of women that are divorced or never married as they reach retirement have increased and will continue to increase. These two phenomena suggest that replacement rates for future retirees will keep changing. To investigate the extent of cohort-to-cohort replacement rate changes for future retirees, we use MINT to project replacement rates for the MBB, LBB, and Gen X cohorts. The results are presented in Tables 5 and 6.
| Marital status and sex | DE1 (1931–1935) | DE2 (1936–1941) | War baby (1942–1947) | EBB (1948–1953) | MBB (1954–1959) | LBB (1960–1965) | Gen X (1966–1975) |
|---|---|---|---|---|---|---|---|
| All individuals | 53 | 49 | 46 | 46 | 45 | 40 | 40 |
| Never married | |||||||
| Men | 47 | 45 | 44 | 43 | 45 | 43 | 41 |
| Women | 52 | 49 | 44 | 44 | 47 | 38 | 39 |
| Currently married | |||||||
| Men | 39 | 39 | 37 | 39 | 38 | 35 | 35 |
| Women | 78 | 68 | 57 | 52 | 49 | 44 | 44 |
| Widowed | |||||||
| Men | 41 | 40 | 40 | 42 | 38 | 37 | 41 |
| Women | 121 | 86 | 81 | 70 | 66 | 58 | 58 |
| Divorced | |||||||
| Men | 44 | 43 | 40 | 41 | 41 | 37 | 36 |
| Women | 66 | 57 | 53 | 52 | 50 | 46 | 44 |
| SOURCE: Authors' calculations based on MINT. | |||||||
| NOTE: "Replacement rate" is defined as the Social Security benefit amount divided by AIME. | |||||||
| Marital status | DE1 (1931–1935) | DE2 (1936–1941) | War baby (1942–1947) | EBB (1948–1953) | MBB (1954–1959) | LBB (1960–1965) | Gen X (1966–1975) |
|---|---|---|---|---|---|---|---|
| All households | 50 | 47 | 45 | 45 | 44 | 39 | 39 |
| Never married | 47 | 47 | 43 | 44 | 45 | 40 | 38 |
| Currently married | |||||||
| Single earner | 53 | 54 | 54 | 54 | 48 | 39 | 38 |
| Two earners | 45 | 43 | 41 | 41 | 40 | 36 | 37 |
| Combined | 47 | 45 | 42 | 42 | 41 | 37 | 37 |
| Widowed | 64 | 60 | 61 | 56 | 53 | 48 | 50 |
| Divorced | 52 | 48 | 46 | 47 | 45 | 41 | 40 |
| SOURCE: Authors' calculations based on MINT. | |||||||
| NOTE: "Replacement rate" is defined as the Social Security benefit amount divided by AIME. | |||||||
Although we use MINT primarily to project outcomes for future retirees, its rich information also allows us to estimate replacement rates for the earlier cohorts, which provides an external comparison to our HRS estimates. Comparing overlapped cohorts shows that MINT and HRS estimates of replacement rates are largely consistent, although MINT estimates are somewhat higher and the estimated decline for the first four cohorts is slightly smaller. For instance, although the HRS data show that replacement rates of currently married households declined from 46 percent to 37 percent (about 20 percent from baseline) between the DE1 and EBB cohorts (Table 3), MINT shows a decline from 47 percent to 42 percent (about 11 percent from baseline, Table 6).
A close look at the demographics of the MINT sample (Table 7) reveals possible sources of the difference. Compared with the HRS (Table 1), the MINT sample is relatively more educated, more likely to be married, and less likely to be divorced or never married. In terms of labor force participation, the women in the HRS sample work more than those in MINT, while the men work less. Consequently, the proportion of women that is eligible for own retired-worker benefits is higher for the HRS sample than for the MINT sample. In addition, across groups, beneficiaries in the HRS have higher AIMEs than those in the MINT, which likely contributes to lower replacement rates on average. This study's scope does not include investigating which of MINT's embedded assumptions lead to these differences, but the differences between MINT and the HRS should be taken into account when assessing projections for future retirees.
| Characteristic | DE1 (1931–1935) | DE2 (1936–1941) | War baby (1942–1947) | EBB (1948–1953) | MBB (1954–1959) | LBB (1960–1965) | Gen X (1966–1975) |
|---|---|---|---|---|---|---|---|
| Percentage distributions | |||||||
| Sex | |||||||
| Men | 46.8 | 47.2 | 47.1 | 46.2 | 46.9 | 47.4 | 47.6 |
| Women | 53.2 | 52.8 | 52.9 | 53.8 | 53.1 | 52.6 | 52.4 |
| Marital status | |||||||
| Married | 73.8 | 72.1 | 68.1 | 63.4 | 61.1 | 60.5 | 58.5 |
| Divorced | 10.6 | 12.9 | 17.6 | 19.4 | 20.1 | 20.3 | 21.0 |
| Never married | 3.5 | 3.8 | 4.8 | 6.5 | 7.7 | 8.2 | 10.3 |
| Widowed | 12.1 | 11.2 | 9.6 | 10.8 | 11.1 | 11.0 | 10.2 |
| Education | |||||||
| Less than high school | 20.6 | 13.9 | 9.0 | 6.4 | 7.3 | 7.2 | 8.1 |
| High school degree | 58.8 | 61.6 | 59.8 | 58.2 | 60.3 | 59.0 | 54.6 |
| At least some college | 20.6 | 24.5 | 31.2 | 35.4 | 32.4 | 33.8 | 37.3 |
| Benefit type (women only) | |||||||
| Retired worker | 44.2 | 55.3 | 59.5 | 67.9 | 70.5 | 71.8 | 75.2 |
| Dually entitled | 31.3 | 28.3 | 27.9 | 23.9 | 21.6 | 20.6 | 17.7 |
| Auxiliary only | 24.5 | 16.4 | 12.6 | 8.2 | 7.9 | 7.7 | 7.1 |
| Cohort average values | |||||||
| Quarters of coverage | |||||||
| Women | |||||||
| Married | 75 | 86 | 99 | 110 | 117 | 119 | 120 |
| Divorced | 106 | 107 | 121 | 129 | 131 | 131 | 129 |
| Never married | 124 | 132 | 132 | 142 | 134 | 140 | 137 |
| Widowed | 84 | 92 | 106 | 113 | 116 | 119 | 117 |
| Men | |||||||
| Married | 141 | 143 | 144 | 143 | 144 | 146 | 142 |
| Divorced | 137 | 135 | 142 | 139 | 144 | 148 | 147 |
| Never married | 127 | 132 | 131 | 136 | 133 | 135 | 140 |
| Widowed | 139 | 141 | 134 | 137 | 141 | 141 | 137 |
| AIME (annual, household level, 2012 dollars) | |||||||
| Marital status | |||||||
| Married | 48,474 | 58,188 | 69,901 | 77,339 | 84,564 | 90,867 | 96,205 |
| Divorced | 24,499 | 28,366 | 35,004 | 36,661 | 41,158 | 44,629 | 49,003 |
| Never married | 25,829 | 31,681 | 37,679 | 40,096 | 40,939 | 43,625 | 51,373 |
| Widowed | 21,491 | 25,465 | 29,014 | 32,608 | 36,855 | 39,889 | 40,475 |
| Benefit amount (annual, household level, 2012 dollars) | |||||||
| Marital status | |||||||
| Married | 22,126 | 25,536 | 28,888 | 31,400 | 33,225 | 32,046 | 33,647 |
| Divorced | 12,397 | 13,012 | 15,620 | 16,360 | 17,543 | 17,063 | 18,148 |
| Never married | 11,290 | 13,533 | 14,908 | 16,043 | 16,260 | 15,209 | 17,291 |
| Widowed | 13,264 | 14,439 | 16,062 | 17,004 | 18,300 | 17,606 | 18,353 |
| Age when claiming (years) | |||||||
| All | 63.5 | 63.4 | 63.9 | 64.3 | 64.1 | 64.1 | 64.1 |
| Men | 63.9 | 63.7 | 64.0 | 64.5 | 64.3 | 64.4 | 64.4 |
| Women | 63.3 | 63.2 | 63.7 | 64.1 | 63.9 | 63.8 | 63.8 |
| Number of observations | 6,460 | 4,820 | 6,041 | 6,962 | 7,676 | 7,590 | 10,966 |
| SOURCE: Authors' calculations based on MINT. | |||||||
| NOTE: Rounded components of percentage distributions do not necessarily sum to 100.0. | |||||||
Current trends suggest a continuing decline in the share of households that will retire as married couples and increasing shares of never-married and divorced households at retirement. Table 7 also shows that the average number of covered quarters generally rises for women in successively younger cohorts. Consequently, more women will be eligible for their own worker benefits at retirement, with the proportion increasing from 68 percent for the EBBs to 75 percent for Gen Xers.
Projections from MINT indicate that the replacement rate will continue to decline for future retirees.17 At the individual level, the replacement rate will decline from 46 percent for EBBs to 40 percent for Gen Xers (Table 5), and at the household level, it will decline from 45 percent to 39 percent (Table 6). Further, for both the earlier and later cohorts, the decline in replacement rates occurs across all income groups, but is more pronounced in the highest income tercile (Table 8). That pattern reflects the influx of highly educated women into the workforce among the two-earner couples.
| Husband's earnings tercile | DE1 (1931–1935) | DE2 (1936–1941) | War baby (1942–1947) | EBB (1948–1953) | MBB (1954–1959) | LBB (1960–1965) | Gen X (1966–1975) |
|---|---|---|---|---|---|---|---|
| Single-earner households | |||||||
| Low | 73 | 72 | 67 | 72 | 52 | 54 | 55 |
| Median | 53 | 52 | 48 | 46 | 44 | 31 | 34 |
| High | 46 | 44 | 46 | 37 | 42 | 33 | 26 |
| Two-earner households | |||||||
| Low | 53 | 53 | 51 | 51 | 49 | 44 | 46 |
| Median | 45 | 43 | 40 | 42 | 41 | 36 | 38 |
| High | 41 | 38 | 37 | 36 | 36 | 31 | 30 |
| Combined households | |||||||
| Low | 58 | 57 | 54 | 53 | 50 | 45 | 47 |
| Median | 46 | 44 | 41 | 42 | 41 | 36 | 37 |
| High | 42 | 39 | 37 | 36 | 36 | 31 | 30 |
| SOURCE: Authors' calculations based on MINT. | |||||||
| NOTE: "Replacement rate" is defined as the Social Security benefit amount divided by AIME. | |||||||
MINT projects that replacement rates will decline more for single-earner households than for two-earner households: From the EBB to the Gen X birth cohorts, replacement rates are projected to drop from 54 percent to 38 percent for single-earner households (Table 6). That sharp decline, which is concentrated in the last two cohorts, is a surprising departure from the experience of older cohorts. The difference is driven primarily by projected changes in the nature of single-earner households. The share of single-earner households in which spouses receive benefits based solely on the husband's earnings record is projected to drop sharply across cohorts, from 72 percent for EBBs to 64 percent for Gen Xers (not shown). At the same time, the share of households in which spouses receive benefits based on the wife's work history will increase. The latter category tends to have lower replacement rates because a husband who is not eligible for Social Security benefits based on his own working history usually has worked more and earned more than a noneligible wife. As a result, a noneligible husband ends up contributing more to the denominator of the replacement rate.
In summary, the analyses using the HRS and the MINT both show declining individual and household replacement rates. Moreover, the simulations indicate that the increasing labor force participation of women will continue to put downward pressure on Social Security replacement rates for future retirees.
Factors Contributing to Replacement Rate Changes
This section presents the decomposition analysis of the factors influencing cross-cohort declines in replacement rates. It describes the Oaxaca-Blinder decomposition model and then presents the decomposition results under actual and hypothetical assumptions about claiming age.
Conceptual Framework
How much of the decline in replacement rates can be explained by changes in women's labor force participation and marriage patterns—as opposed to other major factors, such as the raising of the FRA and early claiming? Claiming behavior may be particularly important because, under the 1983 Amendments to the Social Security Act, the FRA began to rise incrementally from 65 to 67. The actuarial reduction for early claiming means that if younger cohorts do not postpone claiming to keep pace with the scheduled increases in the FRA, they face lower replacement rates than older cohorts, all else equal. Chart 4 shows the magnitude of the decline by comparing the ratio of benefits claimed at age 62 to benefits claimed at FRA by birth year.18 MINT projects that the average actual claiming age will increase from 63.5 for the DE1 cohort to 64.1 for the Gen X cohort (Table 7).19
Legislated changes in FRA and in early eligibility (age 62) retirement benefit as a percentage of full retirement benefit, by birth year
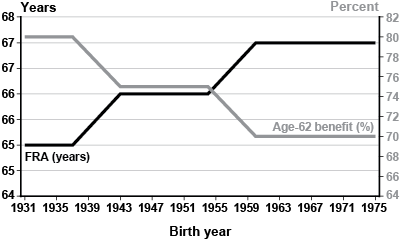
| Birth year | FRA (years) | Age-62 benefit (%) |
|---|---|---|
| 1931 | 65 | 80 |
| 1932 | 65 | 80 |
| 1933 | 65 | 80 |
| 1934 | 65 | 80 |
| 1935 | 65 | 80 |
| 1936 | 65 | 80 |
| 1937 | 65 | 80 |
| 1938 | 65.17 | 79.17 |
| 1939 | 65.33 | 78.33 |
| 1940 | 65.5 | 77.5 |
| 1941 | 65.67 | 76.67 |
| 1942 | 65.83 | 75.83 |
| 1943 | 66 | 75 |
| 1944 | 66 | 75 |
| 1945 | 66 | 75 |
| 1946 | 66 | 75 |
| 1947 | 66 | 75 |
| 1948 | 66 | 75 |
| 1949 | 66 | 75 |
| 1950 | 66 | 75 |
| 1951 | 66 | 75 |
| 1952 | 66 | 75 |
| 1953 | 66 | 75 |
| 1954 | 66 | 75 |
| 1955 | 66.17 | 74.17 |
| 1956 | 66.33 | 73.33 |
| 1957 | 66.5 | 72.5 |
| 1958 | 66.67 | 71.67 |
| 1959 | 66.83 | 70.83 |
| 1960 | 67 | 70 |
| 1961 | 67 | 70 |
| 1962 | 67 | 70 |
| 1963 | 67 | 70 |
| 1964 | 67 | 70 |
| 1965 | 67 | 70 |
| 1966 | 67 | 70 |
| 1967 | 67 | 70 |
| 1968 | 67 | 70 |
| 1969 | 67 | 70 |
| 1970 | 67 | 70 |
| 1971 | 67 | 70 |
| 1972 | 67 | 70 |
| 1973 | 67 | 70 |
| 1974 | 67 | 70 |
| 1975 | 67 | 70 |
To examine the relative contributions of observable characteristics—such as labor force experience, marriage patterns, and claiming behavior—to the gaps in replacement rates between birth cohorts, we use a decomposition method developed by Oaxaca (1973) and Blinder (1973). That method, widely used in social science research, essentially involves calculating what one cohort's outcomes would have looked like if it had the characteristics of another cohort. We estimate the following linear regression to predict household replacement rates for individuals at retirement:
where denotes the household replacement rate for individual i; denotes a set of observed characteristics and a constant, , contains the slope parameters and the intercept; and is a random error term. To explore the difference between two cohorts, we estimate parallel regressions for each cohort:
where C1 denotes cohort 1 and C2 denotes cohort 2, and the error terms and are mean zero. The difference between the mean outcomes of these two cohorts is
By adding and subtracting both and to the right-hand side, the equation can be rewritten as
where is the coefficient from a pooled regression in either cohort (Neumark 1988).20 This equation decomposes the difference in cross-cohort outcomes into the “explained” portion (attributable to differences in the mean of the variables X in the two groups) and the “unexplained” portion (owing to differences in the coefficients between the two groups for the same values of X, including differences in the intercept).21
In the main analysis, the X vector includes three major components that could contribute to the difference across cohorts: marital status (M), labor force participation (L), and claiming behavior (B ratio). The vector for marital status M includes dummies for married, widowed, and divorced; the vector for labor force participation L includes total number of covered quarters, a dummy of whether 40 quarters have been accrued, and a measure of average lifetime earnings.22 B ratio is the outcome of claiming behavior, given the gradually increasing FRA across cohorts; it is constructed as the ratio of actual to full benefits, which differ depending on whether individuals claim early and receive an actuarially reduced benefit, or claim late and receive delayed retirement credits.23 The model also controls for changes over time in the population distribution by education, race, and sex; those factors are grouped in the D vector. Finally, ε is a random error term with mean zero.
Empirical Results
The results of estimating equation (5) are summarized in Table 9, which decomposes the differences in mean replacement rates between cohorts to their contributing factors.24 Overall, the difference in average replacement rates between the oldest cohort (DE1) and the youngest (Gen X) is 12.7 percentage points.25 Changes in labor force activity (and the resulting earnings) explain 31.7 percent of the difference in replacement rates between the oldest and youngest cohorts.26 Moreover, when comparing the oldest cohort (DE1) with its more proximate cohorts, labor force activity accounts for even more of the change—ranging from 31.7 to 74.6 percent. For instance, the labor force activity explains 67.7 percent of the change when comparing the DE1 cohort with the DE2 cohort.
| Difference between DE1 cohort and— | Total decline in mean replacement rate | Decline in replacement rate attributable to— | ||||
|---|---|---|---|---|---|---|
| Demographics a | Marital status | Claiming behavior | Labor force activity | Unexplained factors | ||
| Percentage points | ||||||
| DE2 cohort | 2.4 | 0.2 | 0.1 | 1.1*** | 1.6*** | -0.6 |
| War baby cohort | 5.2 | 0.6*** | 0.0 | 1.7*** | 3.5*** | -0.6 |
| EBB cohort | 5.5 | 0.7*** | -0.4*** | 0.3 | 4.1*** | 0.9** |
| MBB cohort | 7.8 | 0.6*** | -0.5*** | 2.5*** | 4.1*** | 1.1** |
| LBB cohort | 12.8 | 0.8*** | -0.5*** | 4.2*** | 4.5*** | 3.7*** |
| Gen X cohort | 12.7 | 0.6*** | -0.3*** | 4.3*** | 4.0*** | 4.2*** |
| Percentage distribution | ||||||
| DE2 cohort | 100.0 | 8.4 | 2.8 | 47.9 | 67.7 | -26.9 |
| War baby cohort | 100.0 | 12.0 | 0.9 | 31.8 | 67.7 | -12.4 |
| EBB cohort | 100.0 | 12.7 | -7.6 | 4.7 | 74.6 | 15.7 |
| MBB cohort | 100.0 | 7.7 | -6.4 | 32.0 | 52.7 | 14.1 |
| LBB cohort | 100.0 | 5.9 | -3.6 | 33.0 | 35.4 | 29.3 |
| Gen X cohort | 100.0 | 4.5 | -2.7 | 33.7 | 31.7 | 32.8 |
| SOURCE: Authors' calculations based on MINT. | ||||||
| NOTES: "Replacement rate" is defined as the Social Security benefit amount divided by AIME.
Totals do not necessarily equal the sum of rounded components.
* = statistically significant at the 10 percent level.
** = statistically significant at the 5 percent level.
*** = statistically significant at the 1 percent level.
|
||||||
| a. Reflects the combined effects of changes to population distributions by race, sex, and educational attainment over time. | ||||||
Changes in marital patterns over time also affect the replacement rate, but in the opposite direction as the effect of labor force activity—at least, for some cohort pairs, particularly those with greater age differences.27 Because married couples have, on average, lower replacement rates than other groups, a decline in the share of married households leads to an increase in the replacement rate.28 In terms of magnitude, these effects are small yet statistically significant. Changes in marital patterns account for less than 3 percent of the difference in mean replacement rates between the oldest and youngest cohorts in our sample (Table 9).
Given the incremental raising of the FRA, change in claiming behavior over time is also an important factor. It accounts for over one-third of the change in replacement rates between the oldest and the youngest cohorts. The reason claiming behavior exerts such influence is that even though the younger generations are projected to retire later, the delay is not sufficient to keep pace with the increase in the FRA. As a result, MINT expects a larger portion of future retirees to face an actuarial reduction in benefits.
Additionally, changes in demographic factors such as race, sex, and education distributions explain about 5 percent of the total decline in replacement rates between the DE1 and Gen X cohorts. Finally, although differences in three major factors (labor force activity, marital status, and claiming behavior) can account for much of the decline in replacement rates over time, more than 30 percent of the change between the oldest and the youngest cohort remains unexplained. The unexplained component is bigger when comparing cohorts with greater age differences, suggesting that these unexplained factors could in part be driven by the underlying assumptions used for the projections.
We repeated the Oaxaca-Blinder analysis for women only. The results (Table 10) are largely consistent with those for all households, although changes in labor force activity explain a larger fraction of the change in mean replacement rates across cohorts. About half (50.6 percent) of the difference is explained by the changes in labor force activity when comparing replacement rates of the oldest and the youngest cohorts. Further, the unexplained effect is much smaller (15.6 percent), which is consistent with the premise that the changes in replacement rates over time are primarily driven by the changing role of women.
| Difference between DE1 cohort and— | Total decline in mean replacement rate | Decline in replacement rate attributable to— | ||||
|---|---|---|---|---|---|---|
| Demographics a | Marital status | Claiming behavior | Labor force activity | Unexplained factors | ||
| Percentage points | ||||||
| DE2 cohort | 3.3 | 0.2** | 0.1 | 0.9*** | 2.1*** | -0.1 |
| War baby cohort | 5.9 | 0.6*** | 0.2 | 1.1*** | 5.2*** | -1.2** |
| EBB cohort | 7.0 | 0.6** | -0.2 | 0.0 | 7.0*** | -0.5 |
| MBB cohort | 9.0 | 0.7*** | -0.2 | 2.1*** | 7.0*** | -0.6 |
| LBB cohort | 14.1 | 1.0*** | -0.3 | 4.0*** | 7.7*** | 1.7** |
| Gen X cohort | 14.2 | 0.9*** | -0.1 | 4.0*** | 7.2*** | 2.2*** |
| Percentage distribution | ||||||
| DE2 cohort | 100.0 | 7.0 | 3.6 | 28.0 | 63.3 | -1.8 |
| War baby cohort | 100.0 | 10.5 | 3.4 | 18.1 | 88.0 | -20.0 |
| EBB cohort | 100.0 | 8.9 | -2.2 | -0.7 | 100.9 | -6.9 |
| MBB cohort | 100.0 | 7.6 | -2.7 | 23.0 | 78.2 | -6.2 |
| LBB cohort | 100.0 | 7.3 | -2.0 | 28.1 | 54.3 | 12.3 |
| Gen X cohort | 100.0 | 6.1 | -0.7 | 28.5 | 50.6 | 15.6 |
| SOURCE: Authors' calculations based on MINT. | ||||||
| NOTES: "Replacement rate" is defined as the Social Security benefit amount divided by AIME.
Totals do not necessarily equal the sum of rounded components.
* = statistically significant at the 10 percent level.
** = statistically significant at the 5 percent level.
*** = statistically significant at the 1 percent level.
|
||||||
| a. Reflects the combined effects of changes to population distributions by race, sex, and educational attainment over time. | ||||||
Finally, we applied the Oaxaca-Blinder decomposition analysis to different marital-status groups. The results (Table 11) are largely consistent with the previous analyses, except that changing claiming behaviors play a much more important role for the divorced and never-married groups, accounting for nearly 50 percent of the change in replacement rates between the oldest and the youngest cohorts. For the married, the model also controls for spouses' characteristics. Doing so provides further evidence on how marriage, specifically assortative mating, impacts replacement rates.29 The results show that a spouse's claiming behavior and labor force activity are nearly as important as those of the reference person in explaining changes in household replacement rates over time.
| Marital status | Total decline in mean replacement rate | Decline in replacement rate attributable to— | ||||||
|---|---|---|---|---|---|---|---|---|
| Own | Spouse's | Unexplained factors | ||||||
| Demographics a | Claiming behavior | Labor force activity | Demographics a | Claiming behavior | Labor force activity | |||
| Percentage points | ||||||||
| Married | 11.2 | 0.0 | 2.6*** | 2.7*** | 0.2** | 2.2*** | 3.2*** | 0.1 |
| Widowed | 17.7 | 0.4 | 4.9*** | 9.3*** | . . . | . . . | . . . | 3.1** |
| Divorced | 15.0 | 0.2 | 7.3*** | 6.8*** | . . . | . . . | . . . | 0.7 |
| Never married | 17.0 | 0.3 | 8.5*** | 6.0*** | . . . | . . . | . . . | 2.2** |
| Percentage distribution | ||||||||
| Married | 100.0 | 0.1 | 23.5 | 24.4 | 2.0 | 20.0 | 28.2 | 1.3 |
| Widowed | 100.0 | 2.1 | 27.7 | 52.5 | . . . | . . . | . . . | 17.7 |
| Divorced | 100.0 | 1.5 | 48.7 | 45.0 | . . . | . . . | . . . | 4.9 |
| Never married | 100.0 | 1.8 | 49.8 | 35.3 | . . . | . . . | . . . | 13.1 |
| SOURCE: Authors' calculations based on MINT. | ||||||||
| NOTES: "Replacement rate" is defined as the Social Security benefit amount divided by AIME.
Totals do not necessarily equal the sum of rounded components.
. . . = not applicable.
* = statistically significant at the 10 percent level.
** = statistically significant at the 5 percent level.
*** = statistically significant at the 1 percent level.
|
||||||||
| a. Reflects the combined effects of changes to population distributions by race, sex, and educational attainment over time. | ||||||||
Alternative Claiming Behavior Specifications
The results from our main model reveal the importance of individuals' claiming behavior to replacement rates. By design, the variable that captures the effect of claiming behavior, B ratio, reflects the actuarial reduction or delayed retirement credit applied to an individual's full benefit; thus, it is a function of both the age at claiming and the individual's FRA, which has risen over time. Although B ratio does not separate the relative effects of age at claiming and the legislated change in FRA, its combined effect is important to the empirical specification because its omission would confound the estimates of the impacts of labor force activity and marriage rates.
However, to isolate the impacts of our variables of interest from those of claiming and law changes, we compare actual household replacement rates with the rates that would have resulted if all units claimed at FRA (Table 12).30 As expected, we see higher median replacement rates at FRA than at actual claiming age. Further, replacement rates at FRA decline more gradually over time than do those at actual claiming age for all marital-status groups.
| Marital status and claiming age | DE1 (1931–1935) | DE2 (1936–1941) | War baby (1942–1947) | EBB (1948–1953) | MBB (1954–1959) | LBB (1960–1965) | Gen X (1966–1975) |
|---|---|---|---|---|---|---|---|
| All households | |||||||
| Actual claiming age | 50 | 47 | 45 | 45 | 44 | 39 | 39 |
| If claimed at FRA | 55 | 53 | 51 | 51 | 51 | 49 | 49 |
| Never married | |||||||
| Actual claiming age | 47 | 47 | 43 | 44 | 45 | 40 | 38 |
| If claimed at FRA | 53 | 50 | 49 | 48 | 52 | 51 | 49 |
| Currently married | |||||||
| Actual claiming age | 47 | 45 | 42 | 42 | 41 | 37 | 37 |
| If claimed at FRA | 53 | 51 | 48 | 48 | 48 | 45 | 46 |
| Widowed | |||||||
| Actual claiming age | 64 | 60 | 61 | 56 | 53 | 48 | 50 |
| If claimed at FRA | 77 | 70 | 70 | 64 | 63 | 62 | 63 |
| Divorced | |||||||
| Actual claiming age | 52 | 48 | 46 | 47 | 45 | 41 | 40 |
| If claimed at FRA | 55 | 53 | 52 | 53 | 52 | 51 | 50 |
| SOURCE: Authors' calculations based on MINT. | |||||||
| NOTE: "Replacement rate" is defined as the Social Security benefit amount divided by AIME. | |||||||
We estimate decompositions at the FRA to mitigate the effects of potential behavioral responses to the scheduled FRA increase and to provide a robustness check to the earlier estimation results. By defining the FRA replacement rates as the outcome variable, we remove the variable B ratio from the right-hand side of the model and avoid the potentially confounding effects of the previous specification.
Tables 13, 14, and 15 present the estimates for the full sample of households, for women only, and for households by marital status, respectively. With the effect of claiming behavior removed, differences in labor supply (including labor force attachment and earnings) explain over 70 percent of the gap in replacement rates between the DE1 cohort and all subsequent cohorts through the MBBs, and about half of the difference between the DE1 and Gen X cohorts (Table 13). Marital pattern effects are statistically significant but economically small.31 Changing demographics also account for only a small percentage of the difference. Again, nearly one-half of the difference between the DE1 and the last two cohorts remains unexplained by differences in mean characteristics and is instead attributed to the changes in the returns to the factors (that is, due to changes in the coefficient estimates, rather than the differences in mean characteristics) or to unobservable factors.
| Difference between DE1 cohort and— | Total decline in mean replacement rate | Decline in replacement rate attributable to— | |||
|---|---|---|---|---|---|
| Demographics a | Marital status | Labor force activity | Unexplained factors | ||
| Percentage points | |||||
| DE2 cohort | 1.7 | 0.2 | 0.1 | 1.8*** | -0.4 |
| War baby cohort | 4.4 | 0.6*** | 0.1 | 3.9*** | -0.2 |
| EBB cohort | 5.9 | 0.7*** | -0.5*** | 4.6*** | 1.1** |
| MBB cohort | 6.6 | 0.6*** | -0.6*** | 4.7*** | 1.9*** |
| LBB cohort | 10.2 | 0.8*** | -0.6*** | 5.3*** | 4.8*** |
| Gen X cohort | 10.0 | 0.6*** | -0.5*** | 5.0*** | 4.9*** |
| Percentage distribution | |||||
| DE2 cohort | 100.0 | 11.8 | 5.9 | 105.9 | -23.5 |
| War baby cohort | 100.0 | 13.6 | 2.3 | 88.6 | -4.5 |
| EBB cohort | 100.0 | 11.9 | -8.5 | 78.0 | 18.6 |
| MBB cohort | 100.0 | 9.1 | -9.1 | 71.2 | 28.8 |
| LBB cohort | 100.0 | 7.8 | -5.9 | 52.0 | 47.1 |
| Gen X cohort | 100.0 | 6.0 | -5.0 | 50.0 | 49.0 |
| SOURCE: Authors' calculations based on MINT. | |||||
| NOTES: "Replacement rate" is defined as the Social Security benefit amount divided by AIME.
Totals do not necessarily equal the sum of rounded components.
* = statistically significant at the 10 percent level.
** = statistically significant at the 5 percent level.
*** = statistically significant at the 1 percent level.
|
|||||
| a. Reflects the combined effects of changes to population distributions by race, sex, and educational attainment over time. | |||||
| Difference between DE1 cohort and— | Total decline in mean replacement rate | Decline in replacement rate attributable to— | |||
|---|---|---|---|---|---|
| Demographics a | Marital status | Labor force activity | Unexplained factors | ||
| Percentage points | |||||
| DE2 cohort | 3.0 | 0.3** | 0.1 | 2.4*** | 0.2 |
| War baby cohort | 5.6 | 0.8*** | 0.3 | 5.7*** | -1.1* |
| EBB cohort | 7.9 | 0.7*** | -0.2 | 7.9*** | -0.5 |
| MBB cohort | 8.3 | 0.7*** | -0.4* | 8.1*** | 0.0 |
| LBB cohort | 11.7 | 1.2*** | -0.5** | 8.9*** | 2.0** |
| Gen X cohort | 11.7 | 0.9*** | -0.2 | 8.6*** | 2.5*** |
| Percentage distribution | |||||
| DE2 cohort | 100.0 | 10.2 | 4.6 | 78.8 | 6.4 |
| War baby cohort | 100.0 | 13.5 | 4.9 | 101.4 | -19.8 |
| EBB cohort | 100.0 | 9.1 | -2.8 | 99.9 | -6.2 |
| MBB cohort | 100.0 | 8.6 | -5.0 | 96.6 | -0.2 |
| LBB cohort | 100.0 | 10.5 | -4.0 | 76.2 | 17.2 |
| Gen X cohort | 100.0 | 7.4 | -2.0 | 73.6 | 21.0 |
| SOURCE: Authors' calculations based on MINT. | |||||
| NOTES: "Replacement rate" is defined as the Social Security benefit amount divided by AIME.
Totals do not necessarily equal the sum of rounded components.
* = statistically significant at the 10 percent level.
** = statistically significant at the 5 percent level.
*** = statistically significant at the 1 percent level.
|
|||||
| a. Reflects the combined effects of changes to population distributions by race, sex, and educational attainment over time. | |||||
| Marital status | Total decline in mean replacement rate | Decline in replacement rate attributable to— | ||||
|---|---|---|---|---|---|---|
| Own | Spouse's | Unexplained factors | ||||
| Demographics a | Labor force activity | Demographics a | Labor force activity | |||
| Percentage points | ||||||
| Married | 8.9 | -0.2 | 3.4*** | 0.2 | 3.8*** | 1.6*** |
| Widowed | 16.5 | 0.4 | 11.1*** | . . . | . . . | 5.1** |
| Divorced | 11.3 | 0.0 | 8.1*** | . . . | . . . | 3.2** |
| Never married | 11.0 | 0.5 | 7.0*** | . . . | . . . | 3.5** |
| Percentage distribution | ||||||
| Married | 100.0 | -1.9 | 38.3 | 2.0 | 43.4 | 18.3 |
| Widowed | 100.0 | 2.3 | 67.0 | . . . | . . . | 30.7 |
| Divorced | 100.0 | -0.2 | 72.2 | . . . | . . . | 28.0 |
| Never married | 100.0 | 4.1 | 63.9 | . . . | . . . | 32.0 |
| SOURCE: Authors' calculations based on MINT. | ||||||
| NOTES: "Replacement rate" is defined as the Social Security benefit amount divided by AIME.
Totals do not necessarily equal the sum of rounded components.
. . . = not applicable.
* = statistically significant at the 10 percent level.
** = statistically significant at the 5 percent level.
*** = statistically significant at the 1 percent level.
|
||||||
| a. Reflects the combined effects of changes to population distributions by race, sex, and educational attainment over time. | ||||||
In the estimations for women (Table 14), higher labor force participation and earnings account for almost all of the difference in replacement rates between the DE1 and some of the earlier subsequent cohorts, and for about 74 percent of the difference between the DE1 and Gen X cohorts.32
To summarize, decomposing the source of the change in replacement rates over time shows that two factors—changes in labor force activity and in claiming behavior—each explain about one-third of the difference in replacement rates between the oldest and youngest cohorts. When comparing replacement rates at the FRA, labor force participation alone explains about one-half of the difference between the oldest and youngest cohorts and three-fourths or more of the difference between the DE1 and subsequent cohorts through the MBBs. Changes in demographics have produced only small effects, even for marital status, which has changed dramatically over time. A significant share of the change between the oldest and youngest cohorts remains unexplained; that is, not attributable to differences in mean characteristics between the cohorts.
Conclusion
This article examines the extent to which the changing roles of women impacts Social Security replacement rates. We first document substantial changes in women's labor force participation and marital status over time. Then we estimate changes in Social Security replacement rates across a broad range of cohorts that includes claimants born during 1931–1975. We compare estimated replacement rates of current retirees using different data sets and project replacement rates for future retirees. The results show a marked decrease over time in the proportion of preretirement income that Social Security replaces, and the trend—one that is positive for Social Security's finances—will continue for years to come. Over one-third of the decline in replacement rates across cohorts can be explained by the increased labor force activity of women. Surprisingly, trends in marriage patterns account for only a small fraction of the change in replacement rates over time. Much of the remaining explanation rests with the rising FRA and changing claiming behaviors. As life expectancies increase but many people continue to retire in their early sixties, the share of lifetime retirement income provided by Social Security will decline, implying that retirees will have to rely increasingly on other sources of retirement income.
Notes
1 Some recent examples include Butrica, Iams, and Sandell (1999), Butrica and Iams (2000), Favreault, Sammartino, and Steuerle (2002), and Iams and others (2009). Earlier work includes HEW (1979), Burkhauser and Holden (1982), CBO (1986), Ferber (1993), Harrington Meyer (1996), Ross and Upp (1993), and HHS (1985).
2 Results for later cohorts are subject to the uncertainty associated with the projection and should be interpreted with caution.
3 The matched administrative earning records enable accurate calculations of the replacement rates and avoid the reporting errors that are common in public-use surveys.
4 We did not include the HRS' Children of the Depression Era (CODA) cohort, born in the late 1920s. When we first observed individuals of the CODA cohort in 1998, they were aged 68–74, and about 40 percent were widowed. Because of the selection bias due to mortality, the replacement rate calculated using the HRS for the CODA cohort does not represent the replacement rate of all individuals born during that period. Further, for the majority of CODA widow(er)s, we do not have information on their late spouses. Thus, we decided to exclude the CODA cohort from our analysis.
5 The HRS groups all Depression Era respondents into a single combined cohort. We separate that sample into two groups to be consistent with our MINT sample, which is likewise separated into two cohorts and is drawn from two versions of the MINT model (MINT5 and MINT6).
6 To ensure that our cohort estimates are representative and to minimize survival bias, we use two versions of the MINT model—MINT5 and MINT6. Statistics related to the first half of the Depression Era cohort—the DE1 cohort—are derived from MINT5, while the rest of the cohorts are extracted from MINT6. MINT5 derives data from the 1990 to 1996 SIPP, while MINT6 uses the 2001 and 2004 panels of the SIPP. For descriptions of versions 5 and 6 of MINT, see Smith and others (2007, 2010, respectively).
7 To project earnings beyond the last year for which an individual gave permission to match to the administrative data, we again follow Gustman and Steinmeier (2001). For individuals with self-reported earnings, we assume that the average real earnings observed in the last three reported periods persist until their expected claiming date. For respondents who have already claimed Social Security benefits, we use actual claiming age; for those who have not, we assume that respondents claim Social Security benefits at their self-reported expected retirement age. If the expected retirement age was greater than 70, or if the individual indicated that he or she never expected to retire, we use a retirement age of 70 (unless the individual had already worked beyond that age). If the respondent did not provide an expected retirement age, we assign a claiming age so that the age distribution of claiming matches the Social Security–reported claiming ages (SSA 2011, Table 6.B5.1). Combining the actual earnings with the simulated earnings yields a complete earnings profile for each individual in the HRS sample from 1951 to his or her retirement age.
8 In cases where spouses are of different ages, their AIMEs are indexed to different years (although we adjust them for inflation to bring them to same-year dollars that reflect the first year in which both spouses receive benefits). The overall effect of this different indexing on the denominator of the couple's replacement rate depends on the distribution of individual replacement rates between the wife and the husband and on age differences in the population. To the extent that the majority of couples in our data set have wives who are younger, that wives tend to have higher individual replacement rates than husbands, and that wages grow faster than inflation, our household replacement rates for couples might be a bit overstated, as compared with couples having same-year wage indexing.
9 The mortality assumptions imbedded in these calculations start with SSA mortality tables that provide detail by age and sex. We adjust those data, based on Brown, Liebman, and Pollet (2002), to reflect survival probability variations by education and race. We estimate the average mortality rate for each calendar year from 2010 through 2045 (when the youngest Gen X members reach age 70). Then, based on those estimated mortality distributions, we assign a death year to individuals with the lowest survival probability in that specific year. For instance, if 5 percent of the sample is expected to die in 2011, we assign to individuals at the bottom 5 percent of the survival probability distribution a death year of 2011.
10 For individuals who do not have positive lifetime earnings, the replacement rate is undefined.
11 Social Security pays retired-worker benefits to individuals who have accumulated 40 or more quarters of earnings in covered employment over their lives. Therefore, “quarters of coverage” is a crucial factor in benefit eligibility. An individual can earn up to 4 quarters of coverage per year. The amount of earnings that qualified for a quarter of coverage in 2012 was $1,130. Because most jobs are covered by Social Security, quarters of coverage is a good proxy for labor market attachment.
12 See also Table 5.A14 in the Annual Statistical Supplement to the Social Security Bulletin (SSA 2011) for the distribution of women's benefit entitlement over time.
13 We use median replacement rates in order to make the descriptive statistics easily comparable to previous studies and because replacement rates are more prone to outliers—for example, cases where earnings are very low, such as widows and divorced women. That is not a concern for other variables in Table 1.
14 When replacement rates are evaluated at the household level, each married-couple household only counts once, and the household observation is assigned to the husband's birth cohort.
15 Two-earner households include those where one spouse is entitled to benefits based on both his or her own earnings record and his or her spouse's record (“dual entitlement”). In single-earner households, one of the spouses is eligible for auxiliary benefits only.
16 By definition, our measures are censored at the taxable maximum. As a result, they cannot capture the effects at the very top of the earnings distribution.
17 Although declining replacement rates indicate that benefits as a percentage of preretirement earnings are expected to drop, benefits in real terms are expected to keep rising for all household groups (see Table 7).
18 Similarly, because delayed retirement credits accrue only until age 70, the maximum benefit as a percentage of the full retirement benefit will be lower for later cohorts than for earlier cohorts.
19 MINT projects that the claiming age trend will flatten beginning with the EBB cohort, partly because its claiming model does not explicitly build in the rising FRA or cohort effects as covariates in estimation and projection (Smith and others 2010, Table 4-4). However, MINT6 partially accounts for the higher FRA by estimating and simulating two separate models, depending on whether the individual is subject to the retirement earnings test, which in 2000 was suspended for claimants who had reached FRA. As the FRA rises, working individuals in future cohorts will be subject to the retirement earnings test for longer periods in their sixties; thus, they are projected to be more likely to delay claiming. The resulting distribution of claiming ages, of course, will also depend on the extent to which individuals belonging to various sociodemographic groups are likely to work enough to be subject to the retirement earnings test. Smith and others state, “these estimates are based on a sample of individuals for whom the FRA for Social Security ranged from 65 to 66. As the FRA continues to increase to 67, these algorithms automatically slow claiming for higher earners at younger ages (those with earnings above the retirement earnings test exempt amount), but they do not generally slow claiming for lower earners (all else equal).” When interpreting the decomposition results, one should be cautious of the possibility that the current version of MINT might somewhat underestimate the claiming age of younger cohorts.
20 As discussed in the literature, the Oaxaca-Blinder decomposition incurs the index number problem, implying that the decomposition is unstable depending on the choice of the reference group. In order to overcome the index number problem, Neumark proposes a general decomposition based on a pooled regression using the weighted average of two groups. The pooled decomposition has been adopted as the primary approach to measure explained and unexplained gaps in a number of empirical studies (Elder, Goddeeris, and Haider 2010). Although there are other modifications of the Oaxaca-Blinder method, we adopt the Neumark (1988) version in this analysis.
21 Importantly, the unexplained portion also captures all potential effects of differences in unobserved variables.
22 Average lifetime earnings are constructed by averaging the individual's ratio of nominal earnings to the average wage index over his or her working life. Because one's initial Social Security benefits are wage-indexed, this measure directly relates lifetime earnings to the resulting replacement rate.
23 Over time, the B ratio has declined, from 0.90 for the DE1 cohort to 0.83 for the Gen X cohort. The potential endogeneity of the B ratio variable is discussed in the “Alternative Claiming Behavior Specifications” section.
24 For the purpose of consistency, we report the decomposition results using MINT. The results are largely consistent for overlapped cohorts using the HRS data. Detailed regression results, as well as the mean values of the covariates and the results of the pooled regressions, are available upon request from the authors.
25 The Oaxaca-Blinder model decomposes the mean differences in household replacement rates. For married couples, each member is treated as a separate observation, and husband and wife can appear in different birth cohorts. Because the Oaxaca-Blinder methodology decomposes mean differences, Table 9 shows greater replacement rate declines between the oldest and youngest cohort than the declines shown in Table 5, which analyzes medians.
26 We separately control for total number of covered quarters, eligibility (in the form of an indicator of whether 40 quarters have been accrued), and average lifetime earnings in the regression model for simplicity of exposition. Table 9 reports the combined effect of those three components of labor force participation. The separate effect of each component is available from the authors upon request.
27 Although we separately control for three marital statuses (married, widowed, and divorced), the table reports the total effect for those three components of marital patterns. The separate effect of each component is available from the authors upon request.
28 One should note that our measures capture only the percentage of average lifetime earnings that Social Security benefits replace in retirement. An alternative way to compare well-being across households is to use equivalence scales to account for the economies of scale in consumption that married couples enjoy. However, doing so is beyond the scope of this article.
29 The literature has documented substantial changes in assortative mating patterns over time. In addition to the previously mentioned shift in the correlation between spouses' earnings from negative to positive over time, couples are becoming more similar in other dimensions and, rather than “marrying up,” more women are marrying down in terms of education (Rose 2001).
30 A full counterfactual exercise in which all individuals and households claim benefits at FRA involves many assumptions about labor supply, earnings, and potential effects on the average wage index and other macroeconomic variables. Such an exercise is beyond the scope of this article. Instead, for illustrative purposes we calculate benefits at the FRA, adjusted to offset the actuarial reduction for early claiming or the credits for delaying retirement.
31 In the women-only sample, the overall effect of marital status is insignificant for most cohorts (Table 14) because the significant effects on married, widowed, and divorced women (never married is the omitted category) offset each other in magnitude. Detailed decomposition results including the marital groups are available from the authors upon request.
32 We also conducted decomposition analysis using Gen X as the baseline. Although the comparison group in the Gen X-baseline model is subject to significant projection uncertainty, the overall results are consistent with our primary model's finding of strong effects of labor force activity and a much smaller effect of changing marital patterns. The Gen X-baseline model also explains consecutive cohorts better (the unexplained portion is smaller) and in fact shows almost no difference in outcomes between the LBB and Gen X cohorts. Results are available from the authors upon request.
References
Anderson, Patricia M., Alan L. Gustman, and Thomas L. Steinmeier. 1999. “Trends in Male Labor Force Participation and Retirement: Some Evidence on the Role of Pensions and Social Security in the 1970s and 1980s.” Journal of Labor Economics 17(4): 757–783.
Blinder, Alan S. 1973. “Wage Discrimination: Reduced Form and Structural Estimates.” Journal of Human Resources 8(4): 436–455.
BLS. See Bureau of Labor Statistics.
[Board of Trustees] Board of Trustees of the Federal Old-Age and Survivors Insurance and Federal Disability Insurance Trust Funds. 2012. The 2012 Annual Report of the Board of Trustees of the Federal Old-Age and Survivors Insurance and Federal Disability Insurance Trust Funds. Washington, DC: Government Printing Office.
Brown, Jeffrey R., Jeffrey B. Liebman, and Joshua Pollet. 2002. “Estimating Life Tables that Reflect Socioeconomic Differences in Mortality.” In The Distributional Aspects of Social Security and Social Security Reform, edited by Martin Feldstein and Jeffrey B. Liebman, 447–457. Chicago IL: University of Chicago Press.
Bureau of Labor Statistics. 2008. “Highlight of Women's Earnings in 2007.” Report No. 1008. Washington, DC: Department of Labor.
Burkhauser, Richard V., and Karen C. Holden, editors. 1982. A Challenge to Social Security: The Changing Roles of Women and Men in American Society. New York, NY: Academic Press.
Butrica, Barbara A., and Howard M. Iams. 2000. “Divorced Women at Retirement: Projections of Economic Well-Being in the Near Future.” Social Security Bulletin 63(3): 3–12.
Butrica, Barbara A., Howard M. Iams, and Steven H. Sandell. 1999. “Using Data for Couples to Project the Distributional Effects of Changes in Social Security Policy.” Social Security Bulletin 62(3): 20–27.
Butrica, Barbara A., Howard M. Iams, and Karen E. Smith. 2007. “Understanding Baby Boomer Retirement Prospects.” In Redefining Retirement: How Will Boomers Fare?, edited by Brigitte Madrian, Olivia S. Mitchell, and Beth J. Soldo, 70–94. New York, NY: Oxford University Press.
Butrica, Barbara A., and Karen E. Smith. 2012a. “The Impact of Changes in Couples' Earnings on Married Women's Social Security Benefits.” Social Security Bulletin 72(1): 1–10.
———. 2012b. “The Retirement Prospects of Divorced Women.” Social Security Bulletin 72(1): 11–22.
Butrica, Barbara A., Karen E. Smith, and Howard M. Iams. 2012. “This Is Not Your Parents' Retirement: Comparing Retirement Income Across Generations.” Social Security Bulletin 72(1): 37–58.
[CBO] Congressional Budget Office. 1986. Earnings Sharing Options for the Social Security System. Washington, DC: CBO.
Department of Health, Education, and Welfare. 1979. Social Security and the Changing Roles of Men and Women. Washington, DC: Government Printing Office.
Department of Health and Human Services. 1985. Report on Earnings Sharing Implementation Study. Washington, DC: Government Printing Office.
Department of Labor. 2010. “Quick Stats on Women Workers, 2010.” http://www.dol.gov/wb/factsheets /QS-womenwork2010.htm.
Elder, Todd E., John H. Goddeeris, and Steven J. Haider. 2010. “Unexplained Gaps and Oaxaca–Blinder Decompositions.” Labour Economics 17(1): 284–290.
Favreault, Melissa M., Frank J. Sammartino, and C. Eugene Steuerle, editors. 2002. Social Security and the Family: Addressing Unmet Needs in an Underfunded System. Washington, DC: Urban Institute Press.
Ferber, Marianne A. 1993. “Women's Employment and the Social Security System.” Social Security Bulletin 56(3): 33–55.
Gustman, Alan L., and Thomas L. Steinmeier. 2001. “How Effective is Redistribution Under the Social Security Benefit Formula?” Journal of Public Economics 82(1): 1–28.
Haider, Steven, and Gary Solon. 2000. “Nonrandom Selection in the HRS Social Earnings Sample.” Working Paper No. 00-01. Santa Monica, CA: RAND Corporation.
Harrington Meyer, Madonna. 1996. “Making Claims as Workers or Wives: The Distribution of Social Security Benefits.” American Sociological Review 61(3): 449–465.
HEW. See Department of Health, Education, and Welfare.
HHS. See Department of Health and Human Services.
Iams, Howard M., John W. R. Phillips, Kristen Robinson, Lionel P. Deang, and Irena Dushi. 2009. “Cohort Changes in the Retirement Resources of Older Women.” Social Security Bulletin 68(4): 1–13.
Kapteyn, Arie, Pierre-Carl Michaud, James Smith, and Arthur van Soest. 2006. “Effects of Attrition and Non-Response in the Health and Retirement Study.” Working Paper No. WR-407. Santa Monica, CA: RAND Corporation.
Kreider, Rose M., and Renee Ellis. 2011. Number, Timing, and Duration of Marriages and Divorces: 2009. Current Population Reports P70-125. Washington, DC: Census Bureau.
Munnell, Alicia H., Geoffrey Sanzenbacher, and Mauricio Soto. 2007. “Working Wives Reduce Social Security Replacement Rates.” Issue in Brief No. 7-15. Chestnut Hill, MA: Center for Retirement Research at Boston College.
Neumark, David. 1988. “Employers' Discriminatory Behavior and the Estimation of Wage Discrimination.” Journal of Human Resources 23(3): 279–295.
Oaxaca, Ronald. 1973. “Male-Female Wage Differentials in Urban Labor Markets.” International Economic Review 14(3): 693–709.
Purcell, Patrick J. 2012. “Income Replacement Ratios in the Health and Retirement Study.” Social Security Bulletin 72(3): 37–58.
Rose, Elaina. 2001. “Marriage and Assortative Mating: How Have the Patterns Changed?” Working Paper No. 22. Seattle, WA: Center for Statistics and the Social Sciences, University of Washington.
Ross, Jane L., and Melinda M. Upp. 1993. “Treatment of Women in the U.S. Social Security System, 1970–88.” Social Security Bulletin 56(3): 56–67.
Schwartz, Christine. 2010. “Earnings Inequality and the Changing Association between Spouses' Earnings.” American Journal of Sociology 115(5): 1524–1557.
Smith, Karen E., Melissa M. Favreault, Barbara A. Butrica, and Philip Issa. 2010. Modeling Income in the Near Term Version 6. Washington, DC: Urban Institute Press.
Smith, Karen E., Melissa M. Favreault, Caroline Ratcliffe, Barbara Butrica, Eric Toder, Jon M. Bakija. 2007. Modeling Income in the Near Term 5. Washington, DC: Urban Institute Press.
[SSA] Social Security Administration. 2011. Annual Statistical Supplement to the Social Security Bulletin, 2010. Washington, DC: SSA. http://www.socialsecurity.gov/policy/docs/statcomps/supplement/2010/index.html.
———. 2012. Income of the Population 55 or Older, 2010. Washington, DC: SSA. http://www.socialsecurity.gov /policy/docs/statcomps/income_pop55/2010/index.html.